1. Ejercicio - EDP Hiperbólicas
Referencia: Chapra PT8.1 p860, Rodríguez 10.4 p435
Las Ecuaciones Diferenciales Parciales tipo hiperbólicas semejantes a la mostrada, para un ejemplo en particular, representa la ecuación de onda de una dimensión u[x,t], que representa el desplazamiento vertical de una cuerda.
\frac{\partial ^2 u}{\partial t^2}=c^2\frac{\partial ^2 u}{\partial x^2}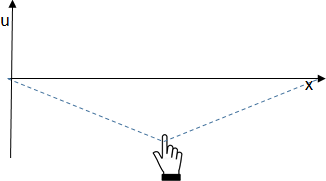
Los extremos de la cuerda de longitud unitaria están sujetos y referenciados a una posición 0 a la izquierda y 1 a la derecha.
u[x,t] , 0<x<1, t≥0
u(0,t) = 0 , t≥0
u(1,t) = 0 , t≥0
Al inicio, la cuerda está estirada por su punto central:
u(x,0) = \begin{cases} -0.5x &, 0\lt x\leq 0.5 \\ 0.5(x-1) &, 0.5\lt x \lt 1 \end{cases}Se suelta la cuerda, con velocidad cero desde la posición inicial:
\frac{\partial u(x,0)}{\partial t} = 02. Desarrollo analítico
La solución se realiza de forma semejante al procedimiento para EDP parabólicas y elípticas. Se cambia a la forma discreta usando diferencias finitas divididas:
\frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{(\Delta t)^2} =c^2 \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2}El error es del orden O(\Delta x)^2 + O(\Delta t)^2.
se reagrupa de la forma:
El término constante, por facilidad se simplifica con el valor de 1
\lambda = \frac{c^2 (\Delta t)^2}{(\Delta x)^2} =1si c = 2 y Δx = 0.2, se deduce que Δt = 0.1
que al sustituir en la ecuación, se simplifica anulando el término u[i,j]:
u_{i,j+1}+u_{i,j-1} = u_{i+1,j}+u_{i-1,j}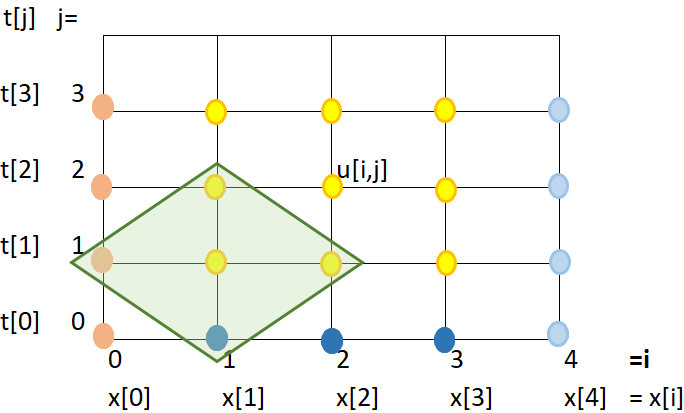
en los que intervienen solo los puntos extremos. Despejando el punto superior del rombo:
u_{i,j+1} = u_{i+1,j}-u_{i,j-1}+u_{i-1,j}Convergencia:
\lambda = \frac{c^2 (\Delta t)^2}{(\Delta x)^2} \leq 1para simplificar aún más el problema, se usa la condición velocidad inicial de la cuerda igual a cero
\frac{\delta u_{i,0}}{\delta t}=\frac{u_{i,1}-u_{i,-1}}{2\Delta t} = 0 u_{i,-1}=u_{i,1}que se usa para cuando el tiempo es cero, permite calcular los puntos para t[1]:
j=0
u_{i,1} = u_{i+1,0}-u_{i,-1}+u_{i-1,0} u_{i,1} = u_{i+1,0}-u_{i,1}+u_{i-1,0} 2 u_{i,1} = u_{i+1,0}+u_{i-1,0} u_{i,1} = \frac{u_{i+1,0}+u_{i-1,0}}{2}Aplicando solo cuando j = 0
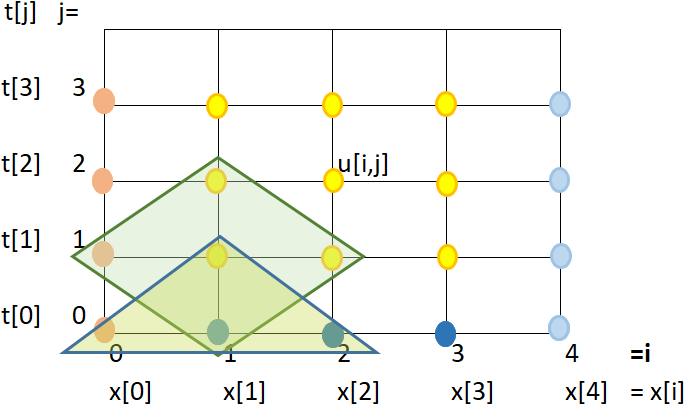
que al ponerlos en la malla se logra un sistema explícito para cada u[i,j], con lo que se puede resolver con un algoritmo:
3. Algoritmo con Python
# Ecuaciones Diferenciales Parciales
# Hiperbólica. Método explicito
import numpy as np
def cuerdainicio(xi):
n = len(xi)
y = np.zeros(n,dtype=float)
for i in range(0,n,1):
if (xi[i]<=0.5):
y[i]=-0.5*xi[i]
else:
y[i]=0.5*(xi[i]-1)
return(y)
# INGRESO
x0 = 0 # Longitud de cuerda
xn = 1
y0 = 0 # Puntos de amarre
yn = 0
t0 = 0 # tiempo inicial
c = 2 # constante EDP
# discretiza
tramosx = 16
tramost = 32
dx = (xn-x0)/tramosx
dt = dx/c
# PROCEDIMIENTO
xi = np.arange(x0,xn+dx/2,dx)
tj = np.arange(0,tramost*dt+dt/2,dt)
n = len(xi)
m = len(tj)
u = np.zeros(shape=(n,m),dtype=float)
u[:,0] = cuerdainicio(xi)
u[0,:] = y0
u[n-1,:] = yn
# Aplicando condición inicial
j = 0
for i in range(1,n-1,1):
u[i,j+1] = (u[i+1,j]+u[i-1,j])/2
# Para los otros puntos
for j in range(1,m-1,1):
for i in range(1,n-1,1):
u[i,j+1] = u[i+1,j]-u[i,j-1]+u[i-1,j]
# SALIDA
np.set_printoptions(precision=2)
print('xi =')
print(xi)
print('tj =')
print(tj)
print('matriz u =')
print(u)
con lo que se obtienen los resultados numéricos,
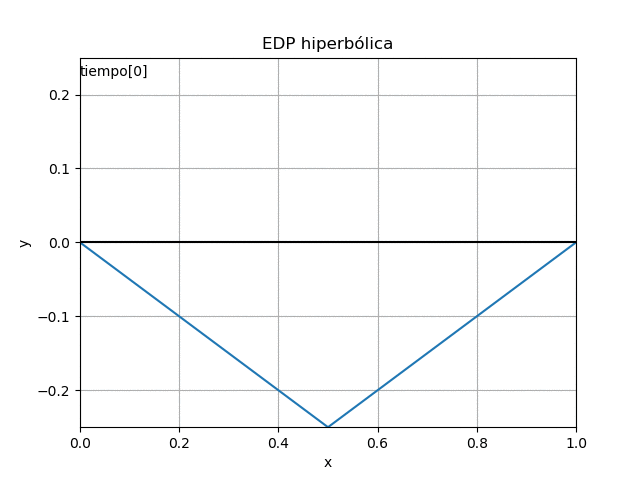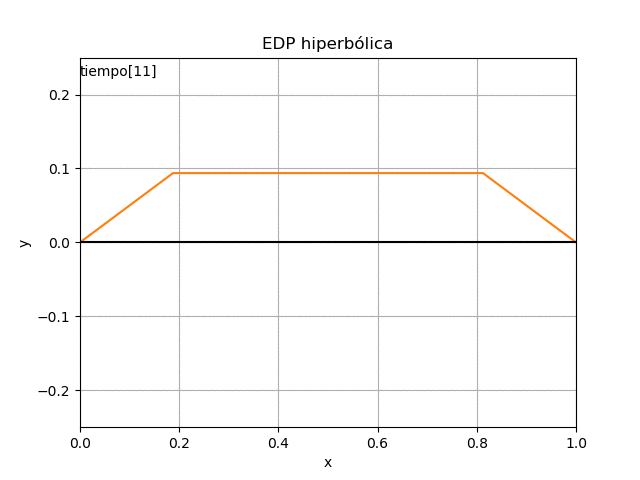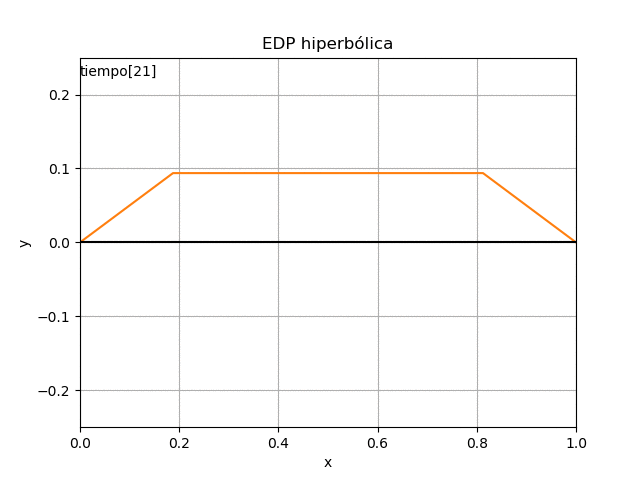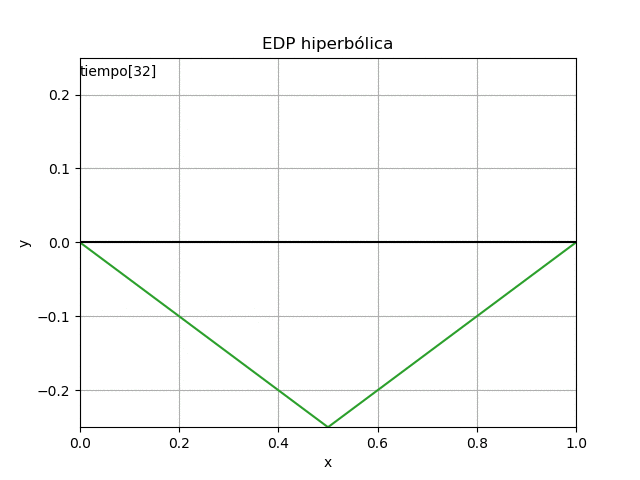
4. Gráfica en Python
Para mejor interpretación se presentan en una gráfica estática y otra animada.
# GRAFICA
import matplotlib.pyplot as plt
for j in range(0,m,1):
y = u[:,j]
plt.plot(xi,y)
plt.title('EDP hiperbólica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
Una vez realizado el algoritmo, se pueden cambiar las condiciones iniciales de la cuerda y se observan los resultados.
gráfica con animación
# **** GRÁFICO CON ANIMACION ***********
import matplotlib.animation as animation
# Inicializa parametros de trama/foto
retardo = 70 # milisegundos entre tramas
tramas = m
maximoy = np.max(np.abs(u))
figura, ejes = plt.subplots()
plt.xlim([x0,xn])
plt.ylim([-maximoy,maximoy])
# lineas de función y polinomio en gráfico
linea_poli, = ejes.plot(xi,u[:,0], '-')
plt.axhline(0, color='k') # Eje en x=0
plt.title('EDP hiperbólica')
# plt.legend()
# txt_x = (x0+xn)/2
txt_y = maximoy*(1-0.1)
texto = ejes.text(x0,txt_y,'tiempo:',
horizontalalignment='left')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
# Nueva Trama
def unatrama(i,xi,u):
# actualiza cada linea
linea_poli.set_ydata(u[:,i])
linea_poli.set_xdata(xi)
linea_poli.set_label('tiempo linea: '+str(i))
texto.set_text('tiempo['+str(i)+']')
# color de la línea
if (i<=9):
lineacolor = 'C'+str(i)
else:
numcolor = i%10
lineacolor = 'C'+str(numcolor)
linea_poli.set_color(lineacolor)
return linea_poli, texto
# Limpia Trama anterior
def limpiatrama():
linea_poli.set_ydata(np.ma.array(xi, mask=True))
linea_poli.set_label('')
texto.set_text('')
return linea_poli, texto
# Trama contador
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(figura,
unatrama,
i ,
fargs=(xi,u),
init_func=limpiatrama,
interval=retardo,
blit=True)
# Graba Archivo video y GIFAnimado :
# ani.save('EDP_hiperbólica.mp4')
ani.save('EDP_hiperbolica.gif', writer='imagemagick')
plt.draw()
plt.show()
Se recomienda realizar otros ejercicios de la sección de evaluaciones para EDP Hiperbólicas y observar los resultados con el algoritmo modificado.