Ejercicio: 2Eva_2021PAOI_T1 Masa transportada por tubo
Las expresiones siguientes se usan dentro de la expresión del integral
Q(t)=9+4 \cos ^2 (0.4t) c(t)=5e^{-0.5t}+2 e^{-0.15 t} M = \int_{t_1}^{t_2} Q(t)c(t) dtliteral a
Usando los valores dados para el intervalo [2,8] con 6 tramos h = (8-2)/6 =1
Se usa los valores de cada ti en Se puede obtener una tabla de valores muestreados para integrar f(t) = Q(i)c(t)
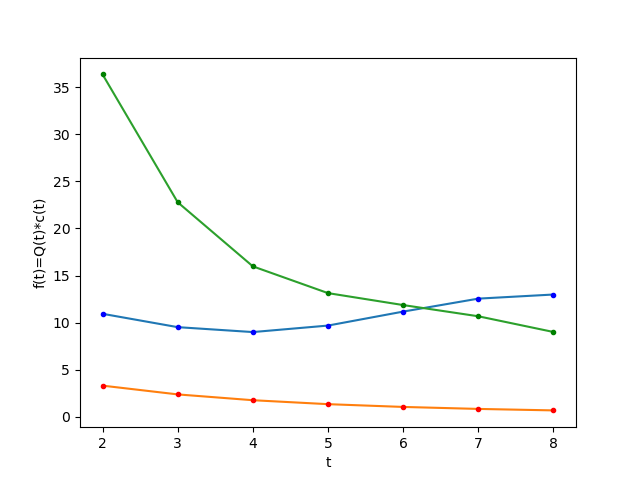
[ti, Qi, Ci, fi] [ 2. 10.9416 3.321 36.3374] [ 3. 9.5252 2.3909 22.7739] [ 4. 9.0034 1.7743 15.9747] [ 5. 9.6927 1.3552 13.1352] [ 6. 11.175 1.0621 11.8687] [ 7. 12.5511 0.8509 10.6793] [ 8. 12.9864 0.694 9.0121]
Para el integral se usan los valores por cada dos tramos
I\cong \frac{1}{3}[36.3374+4(22.7739) + 15.9747] + \frac{1}{3}[15.9747+4(13.1352) + 11.8687] + \frac{1}{3}[11.8687+4(10.6793) + 9.0121] I = 95.7965literal b
L acota de error de truncamiento por cada fórmula usada, se estima como O(h5),
error_{trunca} = -\frac{h^5}{90} f^{(4)}(z)para un valor de z entre [a,b]
por lo que al usar 3 veces la formula de Simpson se podría estimar en:
error_{trunca} = 3(1^5/90) = 0.033literal c
El resultado se puede mejorar de dos formas:
1. Dado que el número de tramos es múltiplo de 3, se puede cambiar la fórmula a Simpon de 3/8, que tendría una cota de error menor
2. Aumentar el número de tramos disminuyendo el valor de h para que el error disminuya. Por ejemplo si se reduce a 0.5, el error disminuye en el orden de 0.55
Podría recomendar la segunda opión, pues a pesar que se aumenta la cota de error por cada vez que se usa la fórmula, el error de cada una disminuye en ordenes de magnitud 0,03125
La gráfica del ejercicio es:
Instrucciones en Python
import numpy as np import matplotlib.pyplot as plt # INGRESO Q = lambda t: 9+4*(np.cos(0.4*t)**2) C = lambda t: 5*np.exp(-0.5*t)+2*np.exp(-0.15*t) t1 = 2 t2 = 8 n = 6 # PROCEDIMIENTO muestras = n+1 dt = (t2-t1)/n ti = np.arange(t1,t2+dt,dt) Qi = Q(ti) Ci = C(ti) fi = Qi*Ci # integración con Simpson 1/3 h= dt I13 = 0 for i in range(0,6,2): S13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2]) I13 = I13 + S13 # SALIDA np.set_printoptions(precision=4) print("[ti,\t Qi,\t Ci,\t fi]") for i in range(0,muestras,1): print(np.array([ti[i],Qi[i],Ci[i],fi[i]])) print("Integral S13: ",I13) # grafica plt.plot(ti,Qi, label = "Q(t)") plt.plot(ti,Ci, label = "c(t)") plt.plot(ti,fi, label = "f(t)") plt.plot(ti,Qi,'.b') plt.plot(ti,Ci,'.r') plt.plot(ti,fi,'.g') plt.xlabel("t") plt.ylabel("f(t)=Q(t)*c(t)") plt.show()