matriz inversa: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
1. Ejercicio
Referencia: Chapra 10.2 p292, Burden 6.3 p292, Rodríguez 4.2.5 Ejemplo 1 p118
Obtener la inversa de una matriz usando el método de Gauss-Jordan, a partir de la matriz:
A = [[4,2,5],
[2,5,8],
[5,4,3]]
matriz inversa: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
2. Desarrollo analítico
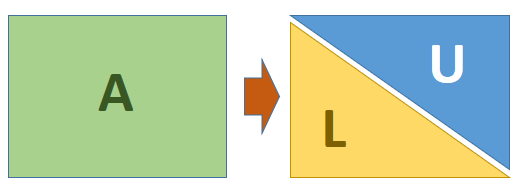
Para el procedimiento, se crea la matriz aumentada de A con la identidad I.
AI = A|I
\begin{pmatrix} 4 & 2 & 5 & 1 & 0 & 0\\ 2 & 5 & 8 & 0 & 1 & 0 \\ 5 & 4 & 3 & 0 & 0 & 1 \end{pmatrix}[[ 4. 2. 5. 1. 0. 0. ] [ 2. 5. 8. 0. 1. 0. ] [ 5. 4. 3. 0. 0. 1. ]]
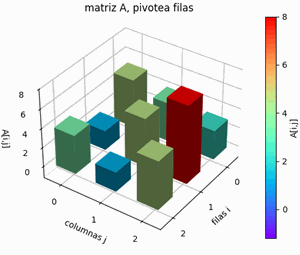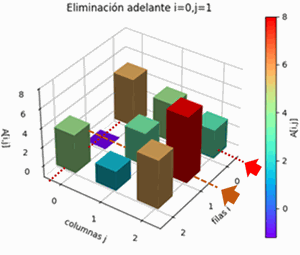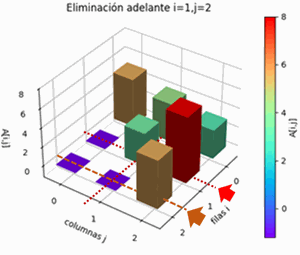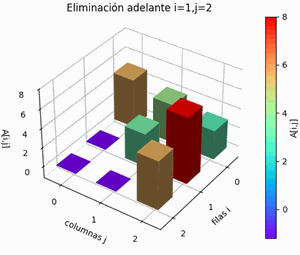
Con la matriz aumentada AI se repiten los procedimientos aplicados en el método de Gauss-Jordan:
- pivoteo parcial por filas
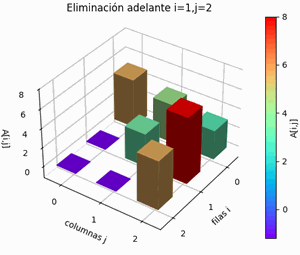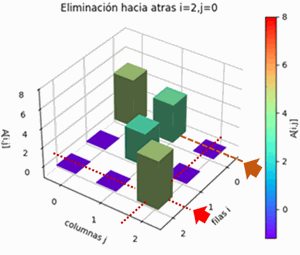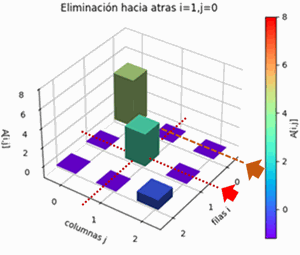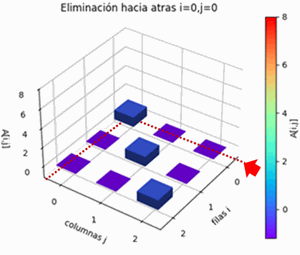
- eliminación hacia adelante
- eliminación hacia atrás
De la matriz aumentada resultante, se obtiene la inversa A-1 en la mitad derecha de AI, lugar que originalmente correspondía a la identidad.
el resultado buscado es:
la matriz inversa es: [[ 0.2 -0.16470588 0.10588235] [-0.4 0.15294118 0.25882353] [ 0.2 0.07058824 -0.18823529]]\begin{pmatrix} 0.2 & -0.16470588 & 0.10588235 \\ -0.4 & 0.15294118 & 0.25882353 \\ 0.2 & 0.07058824 & -0.18823529 \end{pmatrix}
Verifica resultado
El resultado se verifica realizando la operación producto punto entre A y la inversa, que debe resultar la matriz identidad.
A.A-1 = I
El resultado de la operación es una matriz identidad. Observe que los valores del orden de 10-15 o menores se consideran como casi cero o cero.
A.inversa = identidad [[ 1.00000000e+00 -1.38777878e-17 -1.38777878e-16] [ 2.22044605e-16 1.00000000e+00 -2.22044605e-16] [ 5.55111512e-17 -9.71445147e-17 1.00000000e+00]]
matriz inversa: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
3. Algoritmo en Python
El algoritmo que describe el proceso en python:
# Matriz Inversa con Gauss-Jordan # AI es la matriz aumentada A con Identidad import numpy as np # INGRESO A = [[4,2,5], [2,5,8], [5,4,3]] # PROCEDIMIENTO # B = matriz_identidad n,m = np.shape(A) identidad = np.identity(n) np.set_printoptions(precision=4) # 4 decimales en print casicero = 1e-15 # redondear a cero # Matrices como arreglo, numeros reales A = np.array(A,dtype=float) B = np.array(identidad,dtype=float) def pivoteafila(A,B,vertabla=False): ''' Pivoteo parcial por filas, entrega matriz aumentada AB Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) if vertabla==True: print('Matriz aumentada') print(AB) print('Pivoteo parcial:') # Pivoteo por filas AB tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(' ',pivoteado, 'intercambiar filas: ',i, 'con', dondemax+i) if vertabla==True: if pivoteado==0: print(' Pivoteo por filas NO requerido') else: print(AB) return(AB) def gauss_eliminaAdelante(AB,vertabla=False, lu=False,casicero = 1e-15): ''' Gauss elimina hacia adelante tarea: verificar términos cero ''' tamano = np.shape(AB) n = tamano[0] m = tamano[1] if vertabla==True: print('Elimina hacia adelante:') for i in range(0,n,1): pivote = AB[i,i] adelante = i+1 if vertabla==True: print(' fila i:',i,' pivote:', pivote) for k in range(adelante,n,1): if (np.abs(pivote)>=casicero): factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - factor*AB[i,:] for j in range(0,m,1): # casicero revisa if abs(AB[k,j])<casicero: AB[k,j]=0 if vertabla==True: print(' fila k:',k, ' factor:',factor) else: print(' pivote:', pivote,'en fila:',i, 'genera division para cero') if vertabla==True: print(AB) respuesta = np.copy(AB) if lu==True: # matriz triangular A=L.U U = AB[:,:n-1] respuesta = [AB,L,U] return(respuesta) def gauss_eliminaAtras(AB, vertabla=False, inversa=False, casicero = 1e-14): ''' Gauss-Jordan elimina hacia atras Requiere la matriz triangular inferior Tarea: Verificar que sea triangular inferior ''' tamano = np.shape(AB) n = tamano[0] m = tamano[1] ultfila = n-1 ultcolumna = m-1 if vertabla==True: print('Elimina hacia Atras:') for i in range(ultfila,0-1,-1): pivote = AB[i,i] atras = i-1 # arriba de la fila i if vertabla==True: print(' fila i:',i,' pivote:', pivote) for k in range(atras,0-1,-1): if np.abs(AB[k,i])>=casicero: factor = AB[k,i]/pivote AB[k,:] = AB[k,:] - factor*AB[i,:] # redondeo a cero for j in range(0,m,1): if np.abs(AB[k,j])<=casicero: AB[k,j]=0 if vertabla==True: print(' fila k:',k, ' factor:',factor) else: print(' pivote:', pivote,'en fila:',i, 'genera division para cero') AB[i,:] = AB[i,:]/AB[i,i] # diagonal a unos if vertabla==True: print(AB) respuesta = np.copy(AB[:,ultcolumna]) if inversa==True: # matriz inversa respuesta = np.copy(AB[:,n:]) return(respuesta) AB = pivoteafila(A,identidad,vertabla=True) AB = gauss_eliminaAdelante(AB,vertabla=True) A_inversa = gauss_eliminaAtras(AB,inversa=True, vertabla=True) A_verifica = np.dot(A,A_inversa) # redondeo a cero for i in range(0,n,1): for j in range(0,m,1): if np.abs(A_verifica[i,j])<=casicero: A_verifica[i,j]=0 # SALIDA print('A_inversa: ') print(A_inversa) print('verifica A.A_inversa = Identidad:') print(A_verifica)
el resultado buscado es:
Matriz aumentada [[4. 2. 5. 1. 0. 0.] [2. 5. 8. 0. 1. 0.] [5. 4. 3. 0. 0. 1.]] Pivoteo parcial: 1 intercambiar filas: 0 con 2 [[5. 4. 3. 0. 0. 1.] [2. 5. 8. 0. 1. 0.] [4. 2. 5. 1. 0. 0.]] Elimina hacia adelante: fila i: 0 pivote: 5.0 fila k: 1 factor: 0.4 fila k: 2 factor: 0.8 [[ 5. 4. 3. 0. 0. 1. ] [ 0. 3.4 6.8 0. 1. -0.4] [ 0. -1.2 2.6 1. 0. -0.8]] fila i: 1 pivote: 3.4 fila k: 2 factor: -0.3529411764705883 [[ 5. 4. 3. 0. 0. 1. ] [ 0. 3.4 6.8 0. 1. -0.4 ] [ 0. 0. 5. 1. 0.3529 -0.9412]] fila i: 2 pivote: 5.0 [[ 5. 4. 3. 0. 0. 1. ] [ 0. 3.4 6.8 0. 1. -0.4 ] [ 0. 0. 5. 1. 0.3529 -0.9412]] Elimina hacia Atras: fila i: 2 pivote: 5.0 fila k: 1 factor: 1.3599999999999999 fila k: 0 factor: 0.6 [[ 5. 4. 0. -0.6 -0.2118 1.5647] [ 0. 3.4 0. -1.36 0.52 0.88 ] [ 0. 0. 1. 0.2 0.0706 -0.1882]] fila i: 1 pivote: 3.4 fila k: 0 factor: 1.1764705882352942 [[ 5. 0. 0. 1. -0.8235 0.5294] [ 0. 1. 0. -0.4 0.1529 0.2588] [ 0. 0. 1. 0.2 0.0706 -0.1882]] fila i: 0 pivote: 5.0 [[ 1. 0. 0. 0.2 -0.1647 0.1059] [ 0. 1. 0. -0.4 0.1529 0.2588] [ 0. 0. 1. 0.2 0.0706 -0.1882]] A_inversa: [[ 0.2 -0.1647 0.1059] [-0.4 0.1529 0.2588] [ 0.2 0.0706 -0.1882]] verifica A.A_inversa = Identidad: [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
Observe que el algoritmo se pude reducir si usan los procesos de Gauss-Jordan como funciones.
Tarea: Realizar el algoritmo usando una función creada para Gauss-Jordan
matriz inversa: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]
..
4. Función en Numpy
La función en la librería Numpy es np.linalg.inv():
>>> np.linalg.inv(A)
array([[ 0.2 , -0.16470588, 0.10588235],
[-0.4 , 0.15294118, 0.25882353],
[ 0.2 , 0.07058824, -0.18823529]])
>>>
matriz inversa: [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Función ]