EDO con polinomio de Taylor de 3 términos
EDO \frac{\delta y}{\delta x} con Runge-Kutta
EDO \frac{\delta^2 y}{\delta x^2} con Runge-Kutta
Sistemas EDO (f y g) con Runge-Kutta
5.8 Integral y Derivada de f(x), expresiones con Sympy
[ Derivadas f(x) ] [ Derivadas Sin Evaluar ] [ Integral definido [a,b] ] [ Integral Indefinida ]
1. Funciones de prueba
Para los ejemplos se usan f(x) de variable independiente 'x', y constantes 'a' y 'b'
f(x) = a \cos(x) f(x) =a e^{-3x}[ Derivadas f(x) ] [ Derivadas Sin Evaluar ] [ Integral definido [a,b] ] [ Integral Indefinida ]
..
2. Derivadas de f(x) con Sympy
Las expresiones de la derivada se obtienen con la expresión fx.diff(x,k), indicando la k-ésima derivada de la expresión.
f(x): a*exp(-3*x)
f(x) con sym.pprint:
-3⋅x
a⋅ℯ
df/dx: -3*a*exp(-3*x)
df/dx con sym.pprint:
-3⋅x
-3⋅a⋅ℯ
d2f/dx2: 9*a*exp(-3*x)
d2f/dx2 con sym.pprint:
-3⋅x
9⋅a⋅ℯ
Instrucciones en Python
# derivadas de f(x) expresiones Sympy import sympy as sym # INGRESO a = sym.Symbol('a') # constantes sin valor b = sym.Symbol('b') x = sym.Symbol('x',real=True) # variable independente #fx = a*sym.cos(x) fx = a*sym.exp(-3*x) #PROCEDIMIENTO dfx = fx.diff(x,1) d2fx = fx.diff(x,2) # SALIDA print('f(x):',fx) print('f(x) con sym.pprint:') sym.pprint(fx) print('\n df/dx:',dfx) print('df/dx con sym.pprint:') sym.pprint(dfx) print('\n d2f/dx2:',d2fx) print('d2f/dx2 con sym.pprint:') sym.pprint(d2fx)
Referencia: https://docs.sympy.org/latest/tutorials/intro-tutorial/calculus.html#derivatives
Ejemplos:
Polinomio de Taylor – Ejemplos con Sympy-Python
Sistemas LTI CT – Respuesta a entrada cero con Sympy-Python
[ Derivadas f(x) ] [ Derivadas Sin Evaluar ] [ Integral definido [a,b] ] [ Integral Indefinida ]
..
2. Derivadas sin evaluar df(x)/dx con Sympy
Cuando se requiere expresar tan solo la operación de derivadas, que será luego usada o reemplazada con otra expresión, se usa la derivada sin evaluar. Ejemplo:
y = \frac{d}{dx}f(x)Para más adelante definir f(x).
En Sympy, la expresión de y se realiza indicando que f será una variable
x = sym.Symbol('x', real=True)
f = sym.Symbol('f', real=True)
y = sym.diff(f,x, evaluate=False) # derivada sin evaluar
g = sym.cos(x) + x**2
yg = y.subs(f,g).doit() # sustituye f con g y evalua .doit()
>>> y Derivative(f, x) >>> g x**2 + cos(x) >>> yg 2*x - sin(x)
Ejemplos:
EDP Parabólica – analítico con Sympy-Python
EDP Elípticas – analítico con Sympy-Python
EDO lineal – solución complementaria y particular con Sympy-Python
EDO lineal – ecuaciones auxiliar, general y complementaria con Sympy-Python
[ Derivadas f(x) ] [ Derivadas Sin Evaluar ] [ Integral definido [a,b] ] [ Integral Indefinida ]
..
3. Integrales definida de f(x) con Sympy
Sympy incorpora la operación del integral en sus expresiones, que pueden ser integrales definidas en un intervalo o expresiones sin evaluar.
>>> import sympy as sym >>> t = sym.Symbol('t',real=True) >>> fx = 10*sym.exp(-3*t) >>> fx 10*exp(-3*t) >>> y = sym.integrate(fx,(t,0,10)) >>> y 10/3 - 10*exp(-30)/3 >>> y = sym.integrate(fx,(t,0,sym.oo)) >>> y 10/3
[ Derivadas f(x) ] [ Derivadas Sin Evaluar ] [ Integral definido [a,b] ] [ Integral Indefinida ]
..
4. Integrales Indefinida de f(x) con Sympy
La operación se puede realizar con sym.integrate(fx,x), la expresión obtenida no añade la constante.
# integral f(x) eindefinido xpresiones Sympy import sympy as sym # INGRESO a = sym.Symbol('a') # constantes sin valor b = sym.Symbol('b') c = sym.Symbol('c') x = sym.Symbol('x',real=True) # variable independente #fx = a*sym.cos(x) fx = a*sym.exp(-3*x) #PROCEDIMIENTO y = sym.integrate(fx,x) + c # SALIDA print('f(x):',fx) print('f(x) con sym.pprint:') sym.pprint(fx) print('\n y:',y) print('y con sym.pprint:') sym.pprint(y)
con el siguiente resultado:
f(x): a*exp(-3*x)
f(x) con sym.pprint:
-3⋅x
a⋅ℯ
y: -a*exp(-3*x)/3 + c
y con sym.pprint:
-3⋅x
a⋅ℯ
- ─────── + c
3
Referencia: https://docs.sympy.org/latest/modules/integrals/integrals.html
[ Derivadas f(x) ] [ Derivadas Sin Evaluar ] [ Integral definido [a,b] ] [ Integral Indefinida ]
5.7.2 Diferenciación numérica - Tablas con diferencias divididas
Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás] ..
Referencia: Chapra Fig.23.1 p669, Burden 4.1 p167, Rodríguez 8.2,3,4,6 p324
Diferencias divididas hacia adelante
Primera derivada
f'(x_i) = \frac{f(x_{i+1})-f(x_i)}{h} + O(h) f'(x_i) = \frac{-f(x_{i+2})+4f(x_{i+1})-3f(x_i)}{2h} + O(h^2)Segunda derivada
f''(x_i) = \frac{f(x_{i+2})-2f(x_{i+1})+f(x_i)}{h^2} + O(h) f''(x_i) = \frac{-f(x_{i+3})+4f(x_{i+2})-5f(x_{i+1})+2f(x_i)}{h^2} + O(h^2)Tercera derivada
f'''(x_i) = \frac{f(x_{i+3})-3f(x_{i+2})+3f(x_{i+1})-f(x_i)}{h^3} + O(h) f'''(x_i) = \frac{-3f(x_{i+4})+14f(x_{i+3})-24f(x_{i+2})+18f(x_{i+1})-5f(x_i)}{2h^3} + O(h^2)Cuarta derivada
f''''(x_i) = \frac{f(x_{i+4})-4f(x_{i+3})+6f(x_{i+2})-4f(x_{i+1})+f(x_i)}{h^3} + O(h)Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]
Diferencias divididas centradas
Primera derivada
f'(x_i) = \frac{f(x_{i+1})-f(x_{i-1})}{2h} + O(h^2) f'(x_i) = \frac{-f(x_{i+2})+8f(x_{i+1})-8f(x_{i-1}) +f(x_{i-2})}{12h} + O(h^4)Segunda derivada
f''(x_i) = \frac{f(x_{i+1})-2f(x_{i})+f(x_{i-1})}{h^2} + O(h^2) f''(x_i) = \frac{-f(x_{i+2})+16f(x_{i+1})-30f(x_{i})+16f(x_{i-1})-f(x_{i-2})}{12h^2} + O(h^4)Tercera derivada
f'''(x_i) = \frac{f(x_{i+2})-2f(x_{i+1})+2f(x_{i-1})-f(x_{i-2})}{2h^3} + O(h^2) f'''(x_i) = \frac{-f(x_{i+3})+8f(x_{i+2})-13f(x_{i+1})+13f(x_{i-1})-8f(x_{i-2})+f(x_{i-3})}{8h^3} + O(h^4)Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]
Diferencias divididas hacia atrás
Primera derivada
f'(x_i) = \frac{f(x_{i})-f(x_{i-1})}{h} + O(h) f'(x_i) = \frac{3f(x_{i})-4f(x_{i-1})+f(x_{i-2})}{2h} + O(h^2)Segunda derivada
f''(x_i) = \frac{f(x_{i})-2f(x_{i-1})+f(x_{i-2})}{h^2} + O(h) f''(x_i) = \frac{2f(x_{i})-5f(x_{i-1})+4f(x_{i-2})-f(x_{i-3})}{h^2} + O(h^2)Tercera derivada
f'''(x_i) = \frac{f(x_{i})-3f(x_{i-1})+3f(x_{i-2})-f(x_{i-3})}{h^3} + O(h) f'''(x_i) = \frac{5f(x_{i})-18f(x_{i-1})+24f(x_{i-2})-14f(x_{i-3})+3f(x_{i-4})}{2h^3} + O(h^2)Diferencias Divididas [ hacia adelante ] [ centradas ] [hacia atrás]
5.7.1 Diferenciación numérica - Error con df/dx en intervalo
[ compara ] [ resultados ] [ algoritmo ]
..
1. Compara derivadas numéricas con analíticas
Para observar el efecto de disminuir h al aumentar los tramos, se realiza la gráfica de la derivada df/dx analítica versus las derivadas numéricas hacia atrás, hacia centrada y hacia adelante.
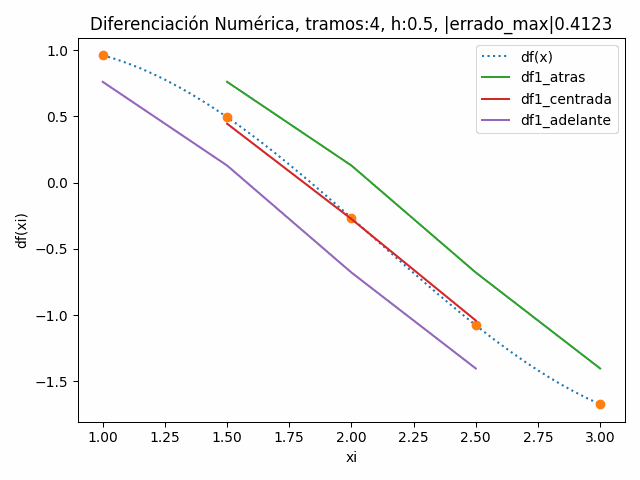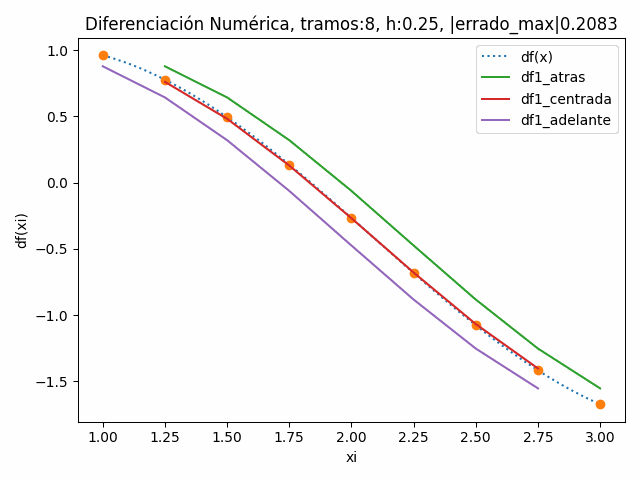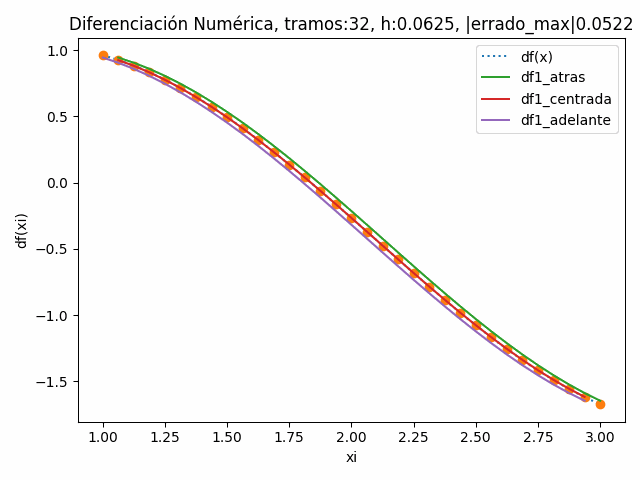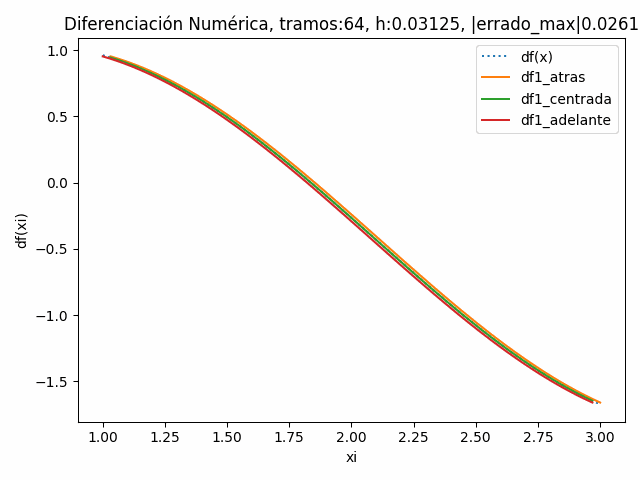Se observa en la animación la reducción del error en cada diferencia dividida.
[ compara ] [ resultados ] [ algoritmo ]
..
2. Resultados del algoritmo
tramos: 4 , h: 0.5 |errado_atras|: 0.3981193548993356 |errado_centro|: 0.04939087954655119 |errado_adelante|: 0.41231110309099034 |errado_max|: 0.41231110309099034 [ dfx, df1_atras, df1_centro, df1_adelante] [[ 0.9610378 nan nan 0.76041177] [ 0.49386065 0.76041177 0.44446977 0.12852777] [-0.26703531 0.12852777 -0.27540932 -0.67934641] [-1.07746577 -0.67934641 -1.04151373 -1.40368104] [-1.67397947 -1.40368104 nan nan]]
tramos: 8 , h: 0.25 |errado_atras|: 0.20757887012431775 |errado_centro|: 0.016528173718511008 |errado_adelante|: 0.20828851979214785 |errado_max|: 0.20828851979214785
tramos: 32 , h: 0.0625 |errado_atras|: 0.05218398011852454 |errado_centro|: 0.0011877802167017393 |errado_adelante|: 0.052183627077393824 |errado_max|: 0.05218398011852454
tramos: 64 , h: 0.03125 |errado_atras|: 0.026094601614190305 |errado_centro|: 0.000302562296112141 |errado_adelante|: 0.026094780174240162 |errado_max|: 094780174240162
[ compara ] [ resultados ] [ algoritmo ]
..
3. Algoritmo con Python
Las instrucciones en Python usadas para la gráfica son:
# Diferenciacion Numerica - 1ra Derivada # Compara resultados en un intervalo import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) dfx = lambda x: np.sin(x)/(2*np.sqrt(x))+ np.sqrt(x)*np.cos(x) a = 1 # intervalo de integracion b = 3 tramos = 64 # >=2, al menos 2 tramos # PROCEDIMIENTO muestras = tramos + 1 h = (b-a)/tramos # puntos de muestras xi = np.linspace(a,b,muestras) fi = fx(xi) # tabla para comparar derivada y diferencias divididas tabla = np.zeros(shape=(muestras,4),dtype=float) for i in range(0,muestras,1): # muestras en intervalo df1_atras = np.nan ; df1_centro = np.nan; df1_adelante = np.nan dfxi = dfx(xi[i]) # derivada analitica, como referencia if i>0 and i<muestras: # hacia Atras, diferencias divididas df1_atras = (fi[i]-fi[i-1])/h if i>0 and i<(muestras-1): # Centro, diferencias divididas df1_centro = (fi[i+1]-fi[i-1])/(2*h) if i>=0 and i<(muestras -1): # hacia Adelante, diferencias divididas df1_adelante = (fi[i+1]-fi[i])/h tabla[i]=[dfxi,df1_atras,df1_centro,df1_adelante] # errado desde dfxi errado_atras = np.max(np.abs(tabla[1:,0]-tabla[1:,1])) errado_centro = np.max(np.abs(tabla[1:muestras-1,0]-tabla[1:muestras-1,2])) errado_adelante = np.max(np.abs(tabla[:muestras-1,0]-tabla[:muestras-1,3])) errado_max = np.max([errado_atras,errado_centro,errado_adelante]) # SALIDA print(' tramos:', tramos,'\t, h:',h,) print('|errado_atras|: ',errado_atras) print('|errado_centro|: ',errado_centro) print('|errado_adelante|:',errado_adelante) print('|errado_max|: ',errado_max) print('[ dfx, df1_atras, df1_centro, df1_adelante]') print(tabla) # GRAFICA import matplotlib.pyplot as plt # fx suave aumentando muestras muestrasfxSuave = tramos*10 + 1 xk = np.linspace(a,b,muestrasfxSuave) dfk = dfx(xk) # Graficar f(x), puntos plt.plot(xk,dfk, label ='df(x)',linestyle='dotted') if tramos<64: plt.plot(xi,tabla[:,0], 'o') # muestras plt.plot(xi,tabla[:,1],label='df1_atras') plt.plot(xi,tabla[:,2],label='df1_centrada') plt.plot(xi,tabla[:,3],label='df1_adelante') plt.xlabel('xi') plt.ylabel('df(xi)') txt = 'Diferenciaci n Num rica' txt = txt + ', tramos:'+str(tramos) txt = txt + ', h:'+str(h) txt = txt + ', |errado_max|'+str(round(errado_max,4)) plt.title(txt) plt.legend() plt.tight_layout() plt.show()
5.7 Diferenciación numérica
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
Referencia: Chapra 23.1 p668, Rodríguez 8.2 p324
La diferenciación numérica aproxima la derivada f'(x) utilizando muestras xi alrededor del punto de interés que se encuentran a distancia h.
Se pueden generar fórmulas por diferencias divididas de alta exactitud
tomando términos adicionales en la expansión de la serie de Taylor. Como referencia, el polinomio de Taylor muestra una aproximación de una función f(x) em el punto x0:
de donde se obtiene la aproximación de las derivadas, al seleccionar la cantidad de términos y despejar, como se mostrará a continuación.
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
1. Primera Derivada con Diferencias divididas hacia adelante
Una aproximación a primera derivada, usa los primeros dos términos del polinomio de Taylor alrededor de xi en para un punto a la derecha xi+1 a una distancia h = xi+1-xi
se puede simplificar en un polinomio de grado uno y un término de error:
f_{i+1} = f_i + (h)f'_i + O(h^2) ...Despejando la expresión para f'i
f'_i = \frac{f_{i+1}-f_i}{h} = \frac{\Delta f_i}{h}
La expresión también es la primera diferencia finita dividida con un error del orden O(h). (tema usado en interpolación).
Revise que el término de la expresión queda O(h2)/h con lo que se disminuye el exponente en uno.
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
2. Primera derivada con diferencias divididas centradas
Se realiza el mismo procedimiento que el anterior, usando un punto xi+1 y xi-1 alrededor de xi. En el término xi-1 el valor de h es negativo al invertir el orden de la resta.
restando la ecuaciones se tiene que
f_{i+1} - f_{i-1} = (h)f'_i +(h)f'_i f_{i+1} - f_{i-1} = 2h f'_iLa expresión de primera derivada usando un punto antes y otro después del punto central queda como:
f'_i = \frac{f_{i+1} - f_{i-1}}{2h}con un error del orden O(h2)
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
..
3. Algoritmo en Python
Compara las diferencias divididas hacia adelante, centro y atrás.
El punto xk para la derivada se encuentra en la posición i , de dónde se toman para el cálculo los puntos xi hacia la izquierda o derecha .
Se requieren al menos 2 tramos para usar las fórmulas, para disponer de un valor de h dentro del intervalo.
Para observar el error en la gráfica, se incorpora f'(x) obtenida de forma analítica como referencia en el ejercicio.
El resultado del algoritmo es:
diferenciación numérica: en xk: 1.5 , h: 0.5 tramos: 4 [ dfx/dx, valor, error] ['df_analítica', 0.4938606479864909, 0] ['df_atras', 0.7604117685484817, 0.2665511205619908] ['df_centro', 0.4444697684399397, -0.04939087954655119] ['df_adelante', 0.12852776833139767, -0.3653328796550932]
Instrucciones en Python
# Diferenciación Numérica - 1ra Derivada # Compara con diferenciación numérica import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) dfx = lambda x: np.sin(x)/(2*np.sqrt(x))+ np.sqrt(x)*np.cos(x) xk = 1.5 # punto derivada a = 1 # intervalo de observación b = 3 tramos = 64 # >=2, al menos 2 tramos # PROCEDIMIENTO # revisa valores, Tarea: incluir en algoritmo cond1 = a<b cond2 = a<xk and xk<b cond3 = tramos>=2 if not(cond1): print('a>b, no es ascendente') if not(cond2): print('ak fuera de intervalo [a,b]') if not(cond3): print('tramos deben ser al menos 2') # tramo menor hacia atras y adelante dx_atras = abs(xk-a) # xk hacia atras intervalo dx_adelante = abs(xk-b) # xk hacia frente intervalo dx_min = min(dx_atras,dx_adelante) h_tramo = (b-a)/tramos h = min(h_tramo,dx_min) xi_atras = np.sort(np.arange(xk,a-h/2,-h)) xi_adelante = np.arange(xk,b+h/2,h) xi = np.concatenate((xi_atras,xi_adelante[1:]),axis=0) i = len(xi_atras)-1 # puntos de muestras fi = fx(xi) tabla = [] # tangentes a xi[i] # derivada analítica, como referencia dfi = dfx(xi[i]) px = lambda x: fi[i] + dfi*(x-xi[i]) pxi = px(xi) tabla.append(['df_analítica',dfi,0,pxi,px]) # hacia Atras, diferencias divididas df1_atras = (fi[i]-fi[i-1])/h px = lambda x: fi[i] + df1_atras*(x-xi[i]) pxi = px(xi) errado = df1_atras - dfi tabla.append(['df_atras',df1_atras,errado,pxi,px]) # Centro, diferencias divididas df1_centro = (fi[i+1]-fi[i-1])/(2*h) px = lambda x: fi[i] + df1_centro*(x-xi[i]) pxi = px(xi) errado = df1_centro - dfi tabla.append(['df_centro',df1_centro,errado,pxi,px]) # hacia Adelante, diferencias divididas df1_adelante = (fi[i+1]-fi[i])/h px = lambda x: fi[i] + df1_adelante*(x-xi[i]) pxi = px(xi) errado = df1_adelante - dfi tabla.append(['df_adelante',df1_adelante,errado,pxi,px]) # SALIDA print('diferenciación numérica:') print('en xk:',xk,'\t, h:',h,) print(' tramos:', tramos) print('[ dfx/dx, valor, error]') for unadifdiv in tabla: print(unadifdiv[0:3])
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
3.1Gráficas en Python
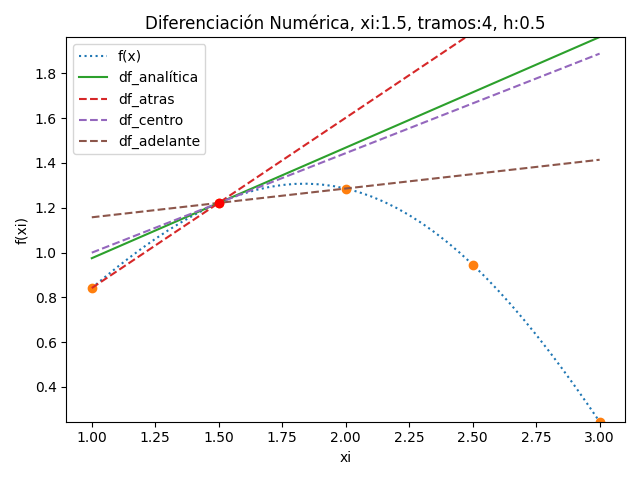Se complementa el algoritmo anterior con las siguientes instrucciones.
# GRAFICA -------------- import matplotlib.pyplot as plt txt = 'Diferenciación Numérica' txt = txt + ', xi:'+str(xk) txt = txt + ', tramos:'+str(tramos) titulo = txt + ', h:'+str(h) # fx suave aumentando muestras muestrasfxSuave = tramos*10 + 1 xk = np.linspace(a,b,muestrasfxSuave) fk = fx(xk) # Graficar f(x), puntos plt.ylim(min(fk),max(fk)*1.5) plt.plot(xk,fk, label ='f(x)',linestyle='dotted') if tramos<64: plt.plot(xi,fi, 'o') # muestras for unadifdiv in tabla: # tangentes a xi[i] linea = 'dashed' if unadifdiv[0]=='df_analítica': linea = 'solid' plt.plot(xi,unadifdiv[3],label=unadifdiv[0], linestyle=linea) plt.plot(xi[i],fi[i],'ro') # punto i observado plt.xlabel('xi') plt.ylabel('f(xi)') plt.title(titulo) plt.legend() plt.tight_layout() plt.show()
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
Segundas derivadas
Al continuar con el procedimiento mostrado se pueden obtener las fórmulas para segundas derivadas, las que se resumen en las tablas de Fórmulas de diferenciación por diferencias divididas.
Diferencias Divididas [ hacia adelante ] [ centradas ] || [ algoritmo ] [ gráfica ]
5.6 Integrales dobles sobre área rectangular con Python
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
1. Integrales Dobles sobre área rectangular
Referencia: Chapra 21.5 p643, Burden 4.9 p174
Un ejemplo sencillo de integral doble es una función sobre un área rectangular. Las técnicas revisadas en las secciones anteriores de pueden reutilizar para la aproximación de integrales múltiples.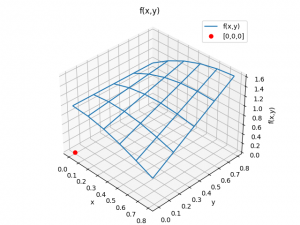 
Considere la integral doble
\int_R \int f(x,y) \delta Asiendo
R = {(x,y) |
x0 ≤ x ≤ xn,
y0 ≤ y ≤ yn }
que es una región rectangular en el plano.
\int_{x_o}^{x_n}\int_{y_o}^{y_n} f(x,y) \delta y \delta x \int_{y_o}^{y_n} \int_{x_o}^{x_n} f(x,y) \delta x \delta y[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
2. Ejercicio
Referencia: 3Eva_IIT2018_T1 Integral doble con Cuadratura de Gauss
Aproxime el resultado de la integral doble (en área rectangular)
\displaystyle \int_{0}^{\pi/4} \displaystyle\int_{0}^{\pi/4} \Big( 2y \sin(x) + \cos ^2 (x) \Big) \delta y \delta xConsidere los tramosx = 5 como tamaños de paso en eje x , tramosy = 4 como tamaños de paso en eje y.
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
3. Desarrollo Analítico
Use las fórmulas compuestas de Simpson, haciendo primero constante un valor en y, luego propagando el proceso. Al obtener los integrales en un sentido, repetir el proceso con los resultados en el otro eje.
j: 0 , yj[0]: 0.0 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.4378989163640264 Simpson 1/3 : 0.20482799857900125 j: 1 , yj[1]: 0.19634954084936207 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.4807008818748735 Simpson 1/3 : 0.2770455037573468 j: 2 , yj[2]: 0.39269908169872414 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.5235028473857204 Simpson 1/3 : 0.34926300893569256 j: 3 , yj[3]: 0.5890486225480862 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.5663048128965673 Simpson 1/3 : 0.42148051411403814 j: 4 , yj[4]: 0.7853981633974483 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.6091067784074142 Simpson 1/3 : 0.4936980192923838 Fórmulas compuestas, tramos: 4 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 1 0] Simpson 3/8 : 0.4802254950852897 trapecio : 0.20524320554554915 xi [0. 0.1571 0.3142 0.4712 0.6283 0.7854] yj [0. 0.1963 0.3927 0.589 0.7854] f(x,y) [[1. 0.9755 0.9045 0.7939 0.6545 0.5 ] [1. 1.037 1.0259 0.9722 0.8853 0.7777] [1. 1.0984 1.1472 1.1505 1.1162 1.0554] [1. 1.1598 1.2686 1.3287 1.347 1.333 ] [1. 1.2213 1.3899 1.507 1.5778 1.6107]] Integral Volumen: 0.6854687006308389
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
4. Algoritmo en Python
El punto de partida es usar las Fórmulas compuestas con Δx segmentos desiguales, donde el algoritmo selecciona aplicar Simpson 3/8, Simpson 1/3 y trapecios según se cumplan los requisitos.
Instrucciones en Python
# 3Eva_IIT2018_T1 Integral doble con Cuadratura de Gauss # Integrales de volumen o dobles import numpy as np # INGRESO fxy = lambda x,y: 2*y*np.sin(x)+(np.cos(x))**2 x0 = 0 # intervalo x xn = np.pi/4 y0 = 0 # intervalo y yn = np.pi/4 tramosx = 5 # tramos por eje tramosy = 4 titulo = 'f(x,y)' precision = 4 # decimales a mostrar # PROCEDIMIENTO xi = np.linspace(x0,xn,tramosx+1) yj = np.linspace(y0,yn,tramosy+1) n = len(xi) m = len(yj) hx = (xn-x0)/tramosx # tamaños de paso hy = (yn-y0)/tramosy Xi,Yj = np.meshgrid(xi,yj) # Matriz u[xi,yj] para f(x,y) F = np.zeros(shape=(n,m),dtype=float) F = fxy(Xi,Yj) def simpson_compuesto(xi,fi,vertabla=False,casicero=1e-7): '''Método compuesto Simpson 3/8, Simpson 1/3 y trapecio salida: integral,cuenta_h ''' # vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) # Método compuesto Simpson 3/8, Simpson 1/3 y trapecio cuenta_h = (-1)*np.ones(n,dtype=int) # sin usar suma = 0 # integral total suma_parcial =[] # integral por cada método i = 0 while i<(n-1): # i<tramos, al menos un tramo tramo_usado = False h = xi[i+1]-xi[i] # tamaño de paso, supone constante # tres tramos iguales if (tramo_usado==False) and (i+3)<n: d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 3/8 S38 = (3/8)*h*(fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]) suma = suma + S38 cuenta_h[i:i+3] = [3,0,0] # Simpson 3/8 suma_parcial.append(['Simpson 3/8',S38]) i = i+3 tramo_usado = True # dos tramos iguales if (tramo_usado==False) and (i+2)<n: d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 1/3 S13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2]) suma = suma + S13 cuenta_h[i:i+2] = [2,0] suma_parcial.append(['Simpson 1/3',S13]) i = i+2 tramo_usado = True # un tramo igual if (tramo_usado == False) and (i+1)<n: trapecio = (h/2)*(fi[i]+fi[i+1]) suma = suma + trapecio cuenta_h[i:i+1] = [1] # usar trapecio suma_parcial.append(['trapecio',trapecio]) i = i+1 tramo_usado = True cuenta_h[n-1] = 0 # ultima casilla if vertabla==True: #mostrar datos parciales print('Fórmulas compuestas, tramos:',n-1) print('métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado') print('tramos iguales en xi:',cuenta_h) for unparcial in suma_parcial: print('',unparcial[0],':',unparcial[1]) return(suma,cuenta_h) # PROGRAMA -------------- areaj = [] cuenta_hj = [] j = 0 # y[0] constante for j in range(0,tramosy+1,1): # cada yj print('j:',j,', yj['+str(j)+']:',yj[j]) xj = Xi[j] fj = F[j] area,cuenta_h=simpson_compuesto(xj,fj, vertabla=True, casicero=1e-7) areaj.append(area) cuenta_hj.append(cuenta_h) area,cuenta_h = simpson_compuesto(yj,areaj, vertabla=True, casicero=1e-7) # SALIDA np.set_printoptions(precision) print('xi',xi) print('yj',yj) print(titulo) print(F) print('Integral Volumen:', area)
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
4. Gráfica de malla
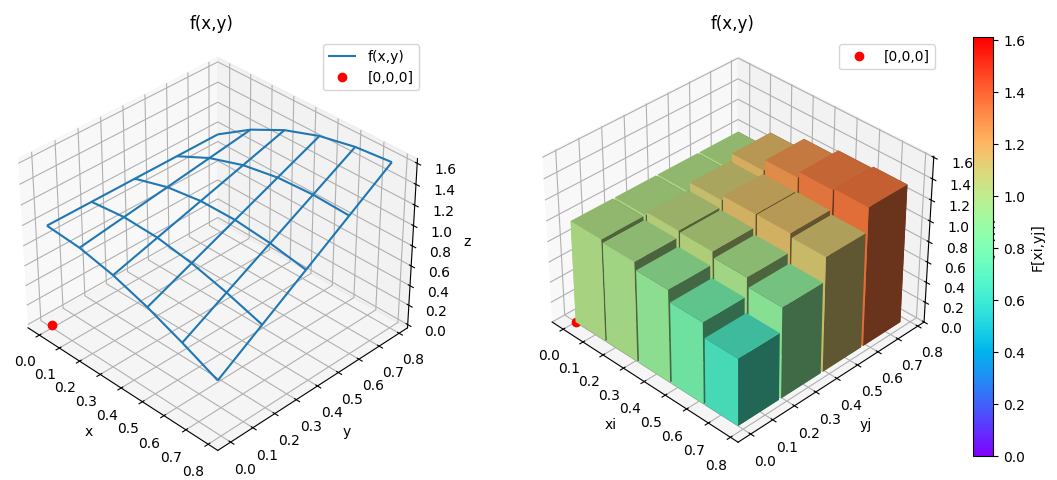
Permite observar la superficie de f(x,y) sobre la que se calculará el volumen respecto al plano x,y en cero.
Instrucciones adicionales al algoritmo
# GRAFICA 3D de malla ------ import matplotlib.pyplot as plt # Malla para cada eje X,Y fig3D = plt.figure() graf3D = fig3D.add_subplot(111, projection='3d') graf3D.plot_wireframe(Xi,Yj,F,label='f(x,y)') graf3D.plot(0,0,0,'ro',label='[0,0,0]') graf3D.set_title(titulo) graf3D.set_xlabel('x') graf3D.set_ylabel('y') graf3D.set_zlabel('z') graf3D.set_title(titulo) graf3D.legend() graf3D.view_init(35, -45) plt.tight_layout() #plt.show()
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
5. Gráfica de barras
Realizado para observar las barras con lados de segmentos dx=hx, dy=hy.
Instrucciones complementarias a la gráfica anterior.
# Grafica barras 3D ------ factor = 0.95 # barra proporcion dx, dy fig_3D = plt.figure() graf_3D = fig_3D.add_subplot(111,projection='3d') F_min = np.min([np.min(F),0]) F_max = np.max([np.max(F)]) color_F = F[:m-1,:n-1].ravel()/F_max color_ij = plt.cm.rainbow(color_F) graf_3D.bar3d(Xi[:m-1,:n-1].ravel(), Yj[:m-1,:n-1].ravel(), np.zeros((n-1)*(m-1)), hx*factor,hy*factor, F[:m-1,:n-1].ravel(), color=color_ij) graf_3D.plot(0,0,0,'ro',label='[0,0,0]') # escala eje z graf_3D.set_zlim(F_min,F_max) # etiqueta graf_3D.set_xlabel('xi') graf_3D.set_ylabel('yj') graf_3D.set_zlabel('z') graf_3D.set_title(titulo) graf_3D.legend() # Barra de color color_escala = plt.Normalize(F_min,F_max) color_barra = plt.cm.ScalarMappable(norm=color_escala, cmap=plt.colormaps["rainbow"]) fig_3D.colorbar(color_barra,ax=graf_3D,label="F[xi,yj]") graf_3D.view_init(35, -45) plt.tight_layout() plt.show()
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
5.5.1 Cuadratura con dos puntos - Experimento con Python
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
..
Cuadratura con dos puntos - Experimento
Para visualizar el concepto de Cuadratura de Gauss de dos puntos considere lo siguiente:
Se tiene un corte transversal del un recipiente rectangular lleno de líquido limitado en x entre [-1,1], al que se le ha depositado encima otro recipiente con perfil f(x) = x2 hasta que reposan sus extremos en x[-1,1].
La altura de ambos recipientes es la misma.
La superficie entre f(x) y el eje x es el integral de f(x) en el intervalo.
Si suponemos que la figura es el corte transversal de una vasija y la parte en amarillo es líquida, la vasija ha desplazado el líquido que ocupa ahora el "área" mostrada en la gráfica que corresponde al integral de f(x)=x2. entre [-1,1].
Ahora, suponga que se perfora el perfil de f(x) en dos puntos equidistantes cercanos x=0. Los orificios permitirían el desplazamiento del liquido al interior de f(x) que dejando pasar suficiente tiempo, permitiría tener todo el líquido en el recipiente rectangular entre [-1,1] como una línea horizontal.
Podría medir la altura que tiene el líquido y que tiene un equivalente en un punto f(x1). Debería encontrar el valor de x1 que permite disponer del mismo valor entre el área debajo de f(x) y el rectángulo del corte transversal amarillo ahora formado.
Se usa el resultado analítico del integral restando el área del rectángulo obtenido al evaluar la función f(x) entre [0,1], teniendo un problema de búsqueda de raíces. Obtenemos el valor de x1.
Se muestra que el área bajo f(x) es equivalente al área del rectángulo conformado.
Si utilizamos el desplazamiento horizontal desde el centro para un punto encontrado como un "factor", tendremos que el área del rectángulo se mantendría equivalente, y el desplazamiento proporcional a la mitad del intervalo si se varía el intervalo de observación. Este factor coincide con el factor de Cuadratura de Gauss de dos puntos.
funcion fx: x**2 Integral Fx: x**3/3 I analitico: 0.6666666666666666 I aproximado: 0.6666666666654123 desplaza centro: 0.5773502691890826 factor desplaza: 0.5773502691890826 Factor CuadGauss: 0.5773502691896258 erradoFactor: 1.2545520178264269e-12 error integral: 1.2543299732215019e-12
El error del integral es del orden de 10-12
Cambiamos la figura geométrica a un trapecio generado por la recta que pasa por los puntos xi desplazados desde el centro.
Usamos la función f(x) = x2 + x + 1, observaremos si los resultado son equivalentes.
La figura al inicio del experimento será:
Luego de realizar realizar el mismo cálculo anterior usando un equivalente a trapecio se tiene:
con valores numéricos:
funcion fx: x**2 + x + 1 Integral Fx: x**3/3 + x**2/2 + x I analitico: 2.6666666666666665 I aproximado: 2.6666666666654124 desplaza centro: 0.5773502691890826 factor desplaza: 0.5773502691890826 Factor CuadGauss: 0.5773502691896258 erradoFactor: 1.2545520178264269e-12 error integral: 1.2541079286165768e-12
El error del integral es también del orden de 10-12, además observe que el factor de cuadratura de Gauss se mantiene.
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
Tarea
Realice el experimento usando un polinomio de grado superior y observe los errores para el integral y las diferencia con el coeficiente de Cuadratura de 2 puntos.
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
Algoritmo con Python
Para resumir la cantidad de instrucciones, se usa el método de la bisección desde la librería Scipy y el subgrupo de funciones de optimización.
Los cálculos para realizar las gráficas se tratan en un bloque luego de mostrar los resultado principales.
# Integración: Cuadratura de Gauss de dos puntos # modelo con varios tramos entre [a,b] # para un solo segmento. import numpy as np import matplotlib.pyplot as plt import sympy as sym import scipy.optimize as op # INGRESO x = sym.Symbol('x') # fx = (x)**2 fx = x**2 + x + 1 # fx = 0.2 + 25.0*x-200*(x**2)+675.0*(x**3)-900.0*(x**4)+400.0*(x**5) a = -1 b = 1 muestras = 51 tolera = 1e-12 iteramax = 100 # PROCEDIMIENTO # Desarrollo analítico con Sympy Fx = sym.integrate(fx,x) Fxn = sym.lambdify('x',Fx,'numpy') Fiab = Fxn(b)-Fxn(a) # Busca igualar trapecio con Integral analitico fxn = sym.lambdify('x',fx,'numpy') base = b-a mitad = base/2 xc = (a+b)/2 # centro diferencia = lambda x: Fiab-base*(fxn(xc-x)+fxn(xc+x))/2 desplazado = op.bisect(diferencia,0,mitad, xtol=tolera,maxiter=iteramax) factor = desplazado/mitad # Integral aproximando con trapecio x0 = xc - factor*mitad x1 = xc + factor*mitad Faprox = base*(fxn(x0)+fxn(x1))/2 # Integral cuadratura Gauss xa = xc + mitad/np.sqrt(3) xb = xc - mitad/np.sqrt(3) FcuadG = base*(fxn(xa)+fxn(xb))/2 erradofactor = np.abs(FcuadG - Faprox) erradoIntegral = np.abs(Fiab-Faprox) # SALIDA print('funcion fx: ', fx) print('Integral Fx: ', Fx) print('I analitico: ', Fiab) print('I aproximado: ', Faprox) print('desplaza centro: ', desplazado) print('factor desplaza: ', factor) print('Factor CuadGauss: ', 1/np.sqrt(3)) print('erradoFactor: ', erradofactor) print('error integral: ', erradoIntegral) # Grafica # Para GRAFICAR # Para gráfica f(x) xi = np.linspace(a,b,muestras) fi = fxn(xi) # Para gráfica Trapecio m = (fxn(x1)-fxn(x0))/(x1-x0) trapeciof = lambda x: fxn(x0)+m*(x-x0) trapecioi = trapeciof(xi) # Areas Trapecio para cada punto que busca k = int(muestras/2) xicg = xi[k:muestras-1] Fcg = [base*(fxn(xi[k+0])+fxn(xi[k-0]))/2] for i in range(1,k,1): untrapecio = base*(fxn(xi[k+i])+fxn(xi[k-i]))/2 Fcg.append(untrapecio) # Punto buscado Fiaprox = base*(fxn(x1)+fxn(x0))/2 Fi = Fxn(xi)-Fxn(a) # Areas de curvas y trapecio plt.subplot(211) # Grafica superior plt.xlim(a,b) plt.plot(xi, fi, label='f(x)') # Solo fi # plt.fill_between(xi,0, fi, # label='integral fi', # color='yellow') # usando cuadratura plt.fill_between(xi,0, trapecioi, label='Cuadratura 2 puntos', color='yellow') plt.axvline(x0,color='white') plt.axvline(x1,color='white') plt.plot([x0,x1],[fxn(x0),fxn(x1)], 'ro', label='x0,x1') plt.axvline(0,color='black') plt.xlabel('x') plt.ylabel('f(x) y Cuadratura de 2 puntos') plt.legend() # Valores de integrales plt.subplot(212) # Grafica inferior plt.xlim(a,b) plt.axhline(Fiab, label='F[a,b]') # plt.plot(xi,Fi,label='F(x)') plt.plot(xicg,Fcg,color='orange',label='Aprox Trapecio') plt.axvline(x1,color='yellow') plt.axvline((1/np.sqrt(3))*(b-a)/2 + xc ,color='magenta') plt.plot(x1,Fiaprox,'ro', label='x0,x1') plt.axvline(0,color='black') plt.xlabel('x') plt.legend() plt.ylabel('Integrando') plt.show()
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
5.5 Cuadratura de Gauss con Python
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
1. Cuadratura de Gauss
Referencia: Chapra 22.3 p655, Rodríguez 7.3 p294, Burden 4.7 p168
La cuadratura de Gauss aproxima el integral de una función en un intervalo [a,b] centrado en cero mediante un cálculo numérico con menos operaciones y evaluaciones de la función. Se representa como una suma ponderada:
I \cong \Big( \frac{b-a}{2} \Big)\Big(c_0f(x_a) + c_1f(x_b)\Big)
para la fórmula de dos puntos con referencia a una función centrada en cero y ancho unitario a cada lado, se tiene:
c_0 = c_1 = 1, x_0 = -\frac{1}{\sqrt{3}}, x_1 = \frac{1}{\sqrt{3}}Para un intervalo de evaluación desplazado en el eje x se requiere convertir los puntos al nuevo intervalo. Se desplaza el punto cero al centro del intervalo [a,b] y se corrige el desplazamiento hacia la izquierda y derecha del centro con x0 y x1.
con lo que el resultado aproximado del integral se convierte en:
I \cong \frac{b-a}{2}(f(x_a) + f(x_b))cuya fórmula es semejante a una mejor aproximación de un trapecio, cuyos promedios de alturas son puntos internos de [a,b], concepto mostrado en la gráfica.
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
2. Ejercicio
Para el ejercicio y comparación de resultado con los otros métodos, se realiza el cálculo para un tramo en el intervalo [a,b].
\int_1^3 \sqrt{x} \sin(x) dx x_a = \frac{3+1}{2} - \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}}\Big)= 1.4226 x_b = \frac{3+1}{2} + \frac{3-1}{2}\Big(\frac{1}{\sqrt{3}} \Big) = 2.5773 f(1.4226) = \sqrt{1.4226} \sin(1.4226) = 1.1796 f(2.5773) = \sqrt{2.5773} \sin(2.5773) = 0.8585con lo que el resultado aproximado del integral se convierte en:
I \cong \frac{3-1}{2}(1.1796 + 0.8585) = 2.0382que usando instrucciones de Python para obtener los valores:
>>> import numpy as np >>> (3+1)/2-(3-1)/2*(1/np.sqrt(3)) 1.4226497308103743 >>> (3+1)/2+(3-1)/2*(1/np.sqrt(3)) 2.5773502691896257 >>> fx = lambda x: np.sqrt(x)*np.sin(x) >>> fx(1.4226) 1.1796544827404145 >>> fx(2.5773) 0.8585957175067221 >>> ((3-1)/2)*(fx(1.4226)+fx(2.5773)) 2.0382
el resultado se puede mejorar aumentando el número de tramos en el intervalo [a,b]. Por ejemplo, el resultado usando 4 tramos el resultado es semejante al usar el método del trapecio con 128 tramos, lo que muestra el ahorro en cálculos entre los métodos
Integral: 2.05357719003 >>>
Concepto:
Ejercicio:
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
3. Algoritmo con Python
Para el ejercicio anterior, usando al 4 segmentos y en cada uno aplicando Cuadratura de Gauss, el integral resultante es:
Factores Gauss-Legendre puntos: 2 xgl: [-0.5773502691896258, 0.5773502691896258] cgl: [1.0, 1.0] tabla por intervalos [a,b] [a,b] : [1. 1.5] xi : [1.10566 1.39434] fi : [0.93979 1.16248] area : 0.5255697290782242 [a,b] : [1.5 2. ] xi : [1.60566 1.89434] fi : [1.26638 1.30494] area : 0.642828854689653 [a,b] : [2. 2.5] xi : [2.10566 2.39434] fi : [1.24843 1.05163] area : 0.5750145898962924 [a,b] : [2.5 3. ] xi : [2.60566 2.89434] fi : [0.82428 0.41638] area : 0.31016401636449004 Integral: 2.0535771900286597
Instrucciones en Python usando la Cuadratura de Gauss de dos puntos para una función f(x):
# Integración: Cuadratura de Gauss de 2 puntos # modelo con varios tramos entre [a,b] import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) a = 1 # intervalo de integración b = 3 tramos = 4 # subintervalos a integrar precision = 5 # decimales en tabla # PROCEDIMIENTO # cuadratura de 2 puntos n_puntos = 2 xgl = [-1/np.sqrt(3),1/np.sqrt(3)] cgl = [1.,1.] # cuadratura de n_puntos, fórmulas Gauss-Legendre #xgl, cgl = np.polynomial.legendre.leggauss(2) x_h = np.linspace(a,b,tramos+1) tabla = {} suma = 0 for k in range(0,tramos,1): a = x_h[k] b = x_h[k+1] centro = (a+b)/2 mitad = (b-a)/2 xa = centro + xgl[0]*mitad xb = centro + xgl[1]*mitad area = ((b-a)/2)*(cgl[0]*fx(xa) + cgl[1]*fx(xb)) tabla[k]= {'[a,b]': np.array([a,b]), 'xi': np.array([xa,xb]), 'fi': np.array([fx(xa),fx(xb)]), 'area':area } suma = suma + area # SALIDA np.set_printoptions(precision) print('Factores Gauss-Legendre puntos:',n_puntos) print('xgl:',xgl) print('cgl:',cgl) print('tabla por intervalos [a,b]') for k in range(0,tramos,1): for entrada in tabla[k]: print(entrada,':',tabla[k][entrada]) print('Integral: ', suma)
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
4. Gráfica por tramos
La gráfica que complementa el resultado anterior, se realiza añadiendo las instrucciones presentadas a continuación.
Considere que la gráfica es útil con pocos tramos en el intervalo[a,b]
# GRAFICA ------------- # concepto con 'pocos' tramos/segmentos import matplotlib.pyplot as plt titulo = 'Cuadratura Gauss-Legendre puntos:'+str(n_puntos) a = np.min(x_h); b = np.max(x_h) muestras_k = tramos*10+1 # fx suave en grafico xk = np.linspace(a,b,muestras_k) fk = fx(xk) # tramos marcas de división for i in range(0,tramos+1,1): plt.axvline(x_h[i],linestyle='dashed', color='tab:gray') for k in range(0,tramos,1): xi = tabla[k]['xi'] fi = tabla[k]['fi'] for i in range(0,n_puntos,1): plt.vlines(xi[i],0,fi[i], linestyle='dotted', color='gray') plt.plot(xi[i],fi[i],'o',color='gray') if n_puntos>2: plt.fill_between(xk,0,fk,color='tab:olive') if n_puntos==2: # recta trapecio for k in range(0,tramos,1): xi = tabla[k]['xi'] fi = tabla[k]['fi'] df = (fi[1]-fi[0])/(xi[1]-xi[0]) # pendiente f0 = fi[0] + df*(x_h[k]-xi[0]) # en xi[i] f1 = fi[0] + df*(x_h[k+1]-xi[0]) # en xi[i+1] plt.fill_between([x_h[k],x_h[k+1]], 0,[f0,f1], color='tab:olive') plt.plot([x_h[k],x_h[k+1]],[f0,f1], linestyle='dashed',color='orange') # linea fx plt.plot(xk,fk, label='f(x)', color = 'blue') plt.title(titulo) plt.xlabel('x') plt.ylabel('f(x)') plt.legend() plt.tight_layout() plt.show()
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
..
5. Tabla Cuadratura de Gauss-Legendre para n puntos
Referencia: Chapra Tabla 22.1 p661, Burden 10Ed Tabla 4.12 p172
Para un integral con intervalo centrado en el origen.
I \cong c_0 f(x_0) + c_1f(x_1) + … + c_{n-1}f(x_{n-1})| Puntos | Factor de ponderación | Argumentos de la función | Error de truncamiento |
| 2 | c0 = 1.0000000 c1 = 1.0000000 |
x0 = - 0.577350269 x1 = 0.577350269 |
≅ f(4)(x ) |
| 3 | c0 = 0.5555556 c1 = 0.8888889 c2 = 0.5555556 |
x0 = - 0.774596669 x1 = 0.0 x2 = 0.774596669 |
≅ f(6)(x ) |
| 4 | c0 = 0.3478548 c1 = 0.6521452 c2 = 0.6521452 c3 = 0.3478548 |
x0 = - 0.861136312 x1 = - 0.339981044 x2 = 0.339981044 x3 = 0.861136312 |
≅f (8)(x ) |
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
6. Función en librería np.polynomial.legendre.leggauss para n_puntos
Referencia: np.polynomial.legendre.leggauss
Para obtener los valores de la tabla, se puede usar la librería Numpy.
import numpy as np # n_puntos Gauss-Legendre n_puntos = 2 xg, cg = np.polynomial.legendre.leggauss(n_puntos) print("xg",xg) print("cg",cg)
que presenta como resultado:
xg [-0.57735027 0.57735027] cg [1. 1.]
donde se puede obtener los valores de la tabla con mas puntos.
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
7. Algoritmo de Gauss-Legendre n_puntos
La gráfica se realiza con la sección gráfica anterior.
# Integración: Cuadratura de Gauss de n_puntos # modelo con varios tramos entre [a,b] import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) a = 1 # intervalo de integración b = 3 n_puntos = 5 # n_puntos>=2 tramos = 3 # subintervalos a integrar precision = 5 # decimales en tabla # PROCEDIMIENTO # cuadratura de n_puntos, fórmulas Gauss-Legendre xgl, cgl = np.polynomial.legendre.leggauss(n_puntos) x_h = np.linspace(a,b,tramos+1) # tramos tabla = {} suma = 0 for k in range(0,tramos,1): a = x_h[k] # intervalo[a,b] b = x_h[k+1] centro = (a+b)/2 mitad = (b-a)/2 xi=[]; fi=[]; suma_gl=0 for j in range(0,n_puntos,1): xj = centro + xgl[j]*mitad fj = fx(xj) suma_gl = suma_gl + cgl[j]*fj xi.append(xj) fi.append(fj) area = ((b-a)/2)*suma_gl tabla[k]= {'[a,b]': np.array([a,b]), 'xi': np.array(xi), 'fi': np.array(fi), 'area':area } suma = suma + area # SALIDA np.set_printoptions(precision) print('Factores Gauss-Legendre puntos:',n_puntos) print('xgl:',xgl) print('cgl:',cgl) print('tabla por intervalos [a,b]') for k in range(0,tramos,1): for entrada in tabla[k]: print(entrada,':',tabla[k][entrada]) print('Integral: ', suma)
resultado del algoritmo:
Factores Gauss-Legendre puntos: 5 xgl: [-0.90618 -0.53847 0. 0.53847 0.90618] cgl: [0.23693 0.47863 0.56889 0.47863 0.23693] tabla por intervalos [a,b] [a,b] : [1. 1.66667] xi : [1.03127 1.15384 1.33333 1.51282 1.63539] fi : [0.87127 0.98214 1.1223 1.2279 1.27616] area : 0.7350121364546989 [a,b] : [1.66667 2.33333] xi : [1.69794 1.82051 2. 2.17949 2.30206] fi : [1.29253 1.30741 1.28594 1.21116 1.12934] area : 0.8369414195585647 [a,b] : [2.33333 3. ] xi : [2.36461 2.48718 2.66667 2.84616 2.96873] fi : [1.07815 0.95996 0.74672 0.4912 0.29637] area : 0.4816765248057005 Integral: 2.053630080818964
La gráfica se realiza con la sección gráfica anterior.
[ Cuadratura Gauss ] [ Ejercicio ] [ Algoritmo 2puntos ] [ gráfica ]
[ tabla puntos ] [ algoritmo n_puntos]
5.4 Fórmulas compuestas con Δx segmentos desiguales con Python
[ Concepto ] [ Algoritmo /función ] [ Gráfica ] [ diferencias entre tramos ]
Referencia: Chapra 21.3 p640
En la práctica, existen muchas situaciones con segmentos o tramos de tamaños desiguales. Por ejemplo, los datos obtenidos en experimentos frecuentemente son de este tipo. Para integración numérica, se busca identificar los segmentos de igual tamaño y aplicar: Simpson 3/8, Simpson 1/3 o trapecio.
El algoritmo se desarrolla al incorporar cada método como integral numérico de "fórmulas compuestas".
[ Concepto ] [ Algoritmo /función ] [ Gráfica ] [ diferencias entre tramos ]
1. Ejercicio
Los datos de ejemplo son:
xi = [1. , 1.22222222, 1.44444444, 1.66666667,
1.88888889, 2.11111111, 2+1/3, 2+1/3+0.2,
2+1/3+0.4, 3. ]
fi = [0.84147098, 1.03905509, 1.19226953, 1.28506615,
1.30542157, 1.24598661, 1.10453193, 0.90952929,
0.65637234, 0.24442702]
[ Concepto ] [ Algoritmo /función ] [ Gráfica ] [ diferencias entre tramos ]
..
2. Algoritmo como función en Python
Los resultados del algoritmo muestran los detalles parciales al aplicar cada método acorde a los requisitos de cada uno en el siguiente orden: Tres tramos iguales permiten aplicar Simpson de 3/8, Dos tramos iguales permiten aplicar Simpson de 1/3, Un tramo desigual le aplica trapecio.
Los métodos usados de identifican por el arreglo de tramos iguales:
Fórmulas compuestas, tramos: 9 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 3 0 0 2 0 1 0] Simpson 3/8 : 0.7350425751495739 Simpson 3/8 : 0.8369852099634817 Simpson 1/3 : 0.3599347620000003 trapecio : 0.1201065813333333 tramos iguales en xi: [3 0 0 3 0 0 2 0 1 0] Integral: 2.0520691284463894
Instrucciones en Python
# Integración Simpson 3/8, Simpson 1/3 y trapecio # tramos no iguales, formulas compuestas import numpy as np # INGRESO xi = [1. , 1.22222222, 1.44444444, 1.66666667, 1.88888889, 2.11111111, 2+1/3, 2+1/3+0.2, 2+1/3+0.4, 3. ] fi = [0.84147098, 1.03905509, 1.19226953, 1.28506615, 1.30542157, 1.24598661, 1.10453193, 0.90952929, 0.65637234, 0.24442702] # PROCEDIMIENTO def simpson_compuesto(xi,fi,vertabla=False,casicero=1e-7): '''Método compuesto Simpson 3/8, Simpson 1/3 y trapecio salida: integral,cuenta_h ''' # vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) # Método compuesto Simpson 3/8, Simpson 1/3 y trapecio cuenta_h = (-1)*np.ones(n,dtype=int) # sin usar suma = 0 # integral total suma_parcial =[] # integral por cada método i = 0 while i<(n-1): # i<tramos, al menos un tramo tramo_usado = False h = xi[i+1]-xi[i] # tamaño de paso, supone constante # tres tramos iguales if (tramo_usado==False) and (i+3)<n: d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 3/8 S38 = (3/8)*h*(fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]) suma = suma + S38 cuenta_h[i:i+3] = [3,0,0] # Simpson 3/8 suma_parcial.append(['Simpson 3/8',S38]) i = i+3 tramo_usado = True # dos tramos iguales if (tramo_usado==False) and (i+2)<n: d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 1/3 S13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2]) suma = suma + S13 cuenta_h[i:i+2] = [2,0] suma_parcial.append(['Simpson 1/3',S13]) i = i+2 tramo_usado = True # un tramo igual if (tramo_usado == False) and (i+1)<n: trapecio = (h/2)*(fi[i]+fi[i+1]) suma = suma + trapecio cuenta_h[i:i+1] = [1] # usar trapecio suma_parcial.append(['trapecio',trapecio]) i = i+1 tramo_usado = True cuenta_h[n-1] = 0 # ultima casilla if vertabla==True: #mostrar datos parciales print('Fórmulas compuestas, tramos:',n-1) print('métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado') print('tramos iguales en xi:',cuenta_h) for unparcial in suma_parcial: print('',unparcial[0],':',unparcial[1]) return(suma,cuenta_h) # usa función area,cuenta_h = simpson_compuesto(xi,fi,vertabla=True) # SALIDA print('tramos iguales en xi:',cuenta_h) print('Integral:',area)
[ Concepto ] [ Algoritmo /función ] [ Gráfica ] [ diferencias entre tramos ]
..
3. Gráfica de segmentos desiguales
En la gráfica se diferencian los métodos aplicados por colores.
Se añaden al algoritmo anterior las siguientes instrucciones,
# GRAFICA --------------------- import matplotlib.pyplot as plt n = len(xi) # muestras tramos = n-1 metodotipo = [['na','grey'], ['Trapecio','lightblue'], ['Simpson 1/3','lightgreen'], ['Simpson 3/8','cyan']] # etiquetas linea plt.plot(xi[0],fi[0],'o', label=metodotipo[1][0], color=metodotipo[1][1]) plt.plot(xi[0],fi[0],'o', label=metodotipo[2][0], color=metodotipo[2][1]) plt.plot(xi[0],fi[0],'o', label=metodotipo[3][0], color=metodotipo[3][1]) # relleno y bordes tipo = 0 for i in range(0,tramos,1): if cuenta_h[i]>0: tipo = cuenta_h[i] plt.fill_between([xi[i],xi[i+1]], [fi[i],fi[i+1]],[0,0], color=metodotipo[tipo][1]) # Divisiones entre tramos for i in range(0,n,1): tipolinea = 'dashed' # inicia un método if cuenta_h[i]==0: tipolinea = 'dotted' # dentro de un método plt.vlines(xi[i],0,fi[i],linestyle=tipolinea, color='orange') # puntos de xi,fi plt.plot(xi,fi,marker='o',linestyle='dashed', color='orange',label='f(xi)') plt.axhline(0,color='black') # eje x plt.xlabel('x') plt.ylabel('f(x)') plt.title('Integral numérico xi,fi con Fórmulas Compuestas') plt.legend() plt.tight_layout() plt.show()
[ Concepto ] [ Algoritmo /función ] [ Gráfica ] [ diferencias entre tramos ]
..
4. Diferencias entre tramos xi
Las diferencias entre tramos pueden ser analizadas con una gráfica, usando operaciones de diferencias finitas.
Resultado del algoritmo:
d1xi: [0.22222222 0.22222222 0.22222223 0.22222222 0.22222222 0.22222222 0.2 0.2 0.26666667] d2xi: [ 2.22044605e-16 9.99999972e-09 -9.99999972e-09 -2.22044605e-16 3.33333361e-09 -2.22222233e-02 -4.44089210e-16 6.66666667e-02] diferencia máxima: 4.440892098500626e-16 en i: 7 tramos iguales en xi: [3 0 0 2 0 1 2 0 1 0]
Instrucciones en Python
# revisa xi por # tramos equidistantes y no iguales import numpy as np # INGRESO xi = [1. , 1.22222222, 1.44444444, 1.66666667, 1.88888889, 2.11111111, 2+1/3, 2+1/3+0.2, 2+1/3+0.4, 3. ] # PROCEDIMIENTO casicero=1e-7 # vectores como arreglo, números reales xi = np.array(xi,dtype=float) n = len(xi) # diferencias finitas en xi d1xi = np.diff(xi,1) # magnitud de tramos d2xi = np.diff(xi,2) # diferencia entre tramos errado = np.max(np.abs(d2xi)) # error mayor donde = np.argmax(np.abs(d2xi)) # donde es error mayor # revisa tramos iguales cuenta_h = -1*np.ones(n,dtype=int) i = 0 while i<(n-1): # i<tramos, al menos un tramo tramo_usado = False # tres tramos iguales if (tramo_usado==False) and (i+3)<n: d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 3/8 cuenta_h[i:i+3] = [3,0,0] i = i+3 tramo_usado==True # dos tramos iguales if (tramo_usado==False) and (i+2)<n: d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 1/3 cuenta_h[i:i+2] = [2,0] i = i+2 tramo_usado = True # un tramo igual if (tramo_usado == False) and (i+1)<n: cuenta_h[i:i+1] = [1] # usar trapecio i = i+1 tramo_usado = True cuenta_h[n-1] = 0 # ultima casilla # SALIDA print('d1xi:',d1xi) print('d2xi:',d2xi) print('diferencia máxima:',errado,' en i:',donde) print('tramos iguales en xi:',cuenta_h) # GRAFICA import matplotlib.pyplot as plt m = len(xi)-1 plt.subplot(311) # diferencia entre tramos plt.stem(d2xi,linefmt=':',markerfmt ='C03') plt.plot(np.ones(n)*casicero,color='red',linestyle='dotted') plt.xlim(-0.1,m+0.1) plt.ylabel('diferencia tramos') plt.title('Diferencia entre tramos, muestras:'+str(n)) plt.subplot(312) # tramos plt.stem(d1xi,linefmt=':',markerfmt ='C02') plt.xlim(-0.1,m+0.1) plt.ylabel('|tramo|') plt.subplot(313) # muestras plt.stem(xi,linefmt=':',markerfmt ='C01') plt.xlim(-0.1,m+0.1) plt.ylabel('xi') plt.xlabel('muestra i') plt.tight_layout() plt.show()
[ Concepto ] [ Algoritmo /función ] [ Gráfica ] [ diferencias entre tramos ]
5.3 Regla de Simpson 3/8 con Python
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..
1. Regla de Simpson 3/8
Referencia: Chapra 21.2.1 p.631, Burden 4.2 p147, Rodríguez 7.1.8 p288
I\cong \frac{3h}{8}[f(x_0)+3f(x_1) +3 f(x_2)+f(x_3)]
Es el resultado cuando para el integral se utiliza el resultado de una interpolación con polinomio de tercer grado.
I = \int_a^b f(x) \delta x I \cong \int_a^b f_3 (x) \delta xAl desarrollar la fórmula de la Regla de Simpson de 3/8 para un segmento con tres tramos con distancia h:
I\cong \frac{3h}{8}[f(x_0)+3f(x_1) +3 f(x_2)+f(x_3)]siendo el tramo de un segmento [a,b]
h=\frac{b-a}{3}Error de Truncamiento
error_{truncamiento} = -\frac{3}{80} h^5 f^{(4)} (z)donde z se encuentra entre [a,b]
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..
2. Ejercicio
Para integrar la función en el intervalo [1,3] con 6, 18, 24 y 72 tramos,
f(x)= \sqrt {(x)} \sin(x) 1 \leq x \leq 3Para el ejercicio planteado en la regla de trapecio, usando seis tramos, se aplica el método cada tres tramos.
tramos = 6
h = \frac{3-1}{6} = \frac{1}{3} I\cong \frac{3}{8}\Big(\frac{1}{3}\Big)[f(1)+3f\Big(1+\frac{1}{3}\Big) +3f\Big(1+\frac{2}{3}\Big) + f(2)] + + \frac{3}{8}\Big(\frac{1}{3}\Big)[f(2)+3f\Big(2+\frac{1}{3}\Big) +3f\Big(2+\frac{2}{3}\Big)+ f(3)] f(1)= \sqrt {(1)} \sin(1) = 0.8414 f(4/3)= \sqrt {(4/3)} \sin(4/3) = 1.1222 f(5/3)= \sqrt {(5/3)} \sin(5/3) = 1.2850 f(2)= \sqrt {(2)} \sin(2) = 1.2859 f(7/3)= \sqrt {(7/3)} \sin(7/3) = 1.1045 f(8/3)= \sqrt {(8/3)} \sin(8/3) = 0.7467 f(3)= \sqrt {(3)} \sin(3) = 0.2444 I\cong \frac{3}{24}[0.8414+3(1.1222)+3(1.2850)+1.2859] + \frac{3}{24}[1.2859+3(1.1045)+3(0.7467)+0.2444] I\cong 2.0542las muestras para el ejercicio son:
>>> import numpy as np
>>> fx = lambda x: np.sqrt(x)*np.sin(x)
>>> xi = [1, 1+1/3, 1+2/3, 2, 1+4/3, 1+5/3, 3]
>>> fx(xi)
array([0.84147098, 1.12229722, 1.28506615, 1.28594075,
1.10453193, 0.74672307, 0.24442702]
>>> I1=(3/8)*(1/3)*(fx(1)+3*fx(1+1/3)+3*fx(1+2/3)+fx(2))
>>> I2=(3/8)*(1/3)*(fx(2)+3*fx(1+4/3)+3*fx(1+5/3)+fx(3))
>>> I1+I2
2.0542043270535757
>>>
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..
3. Algoritmo en Python para f(x)
A partir del algoritmo para Simpson de 1/3, se realizan modificaciones para obtener el algoritmo de Simpson de 3/8:
Resultados de algoritmo
tramos: 3 Integral fx con Simpson 3/8: 2.0636730597016992
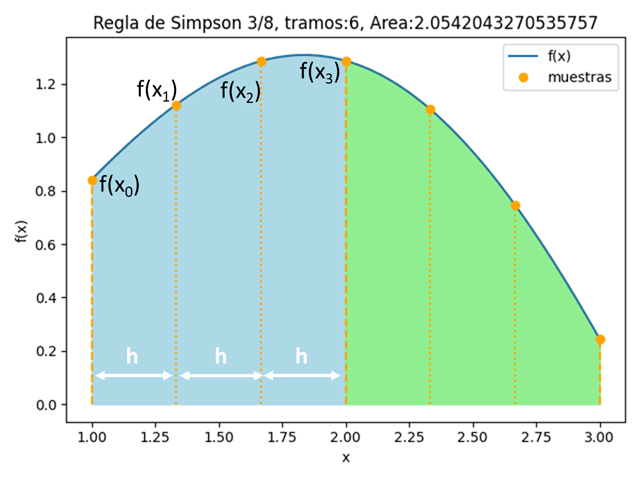
tramos: 6 Integral con Simpson 3/8: 2.0542043270535757
tramos: 9 Integral fx con Simpson 3/8: 2.053741914538051
tramos: 12 Integral fx con Simpson 3/8: 2.0536653010019474
Caso: f(x) es una expresión matemática
# Regla Simpson 3/8 para f(x) entre [a,b],tramos import numpy as np # INGRESO fx = lambda x: np.sqrt(x)*np.sin(x) a = 1 # intervalo de integración b = 3 tramos = 6 # multiplo de 3 # validar: tramos debe ser múltiplo de 3 while tramos%3 >0: print('tramos: ',tramos) txt = 'tramos debe ser múltiplo de 3:' tramos = int(input(txt)) # PROCEDIMIENTO muestras = tramos + 1 xi = np.linspace(a,b,muestras) fi = fx(xi) # Regla de Simpson 3/8 h = (b-a)/tramos suma = 0 # integral numérico for i in range(0,tramos-2,3): #muestras-3 S38 = (3/8)*h*(fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]) suma = suma + S38 # SALIDA print('tramos:', tramos) print('Integral fx con Simpson 3/8: ', suma)
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..
4. Gráfica para integral f(x) con Simpson 3/8
Se puede observar mejor lo expresado usando la gráfica para observar los tramos, muestras, por segmento.
Se puede cambiar el número de tramos en el algoritmo anterior, considerando que deben ser múltiplo de 3.
Instrucciones en Python adicionales al algoritmo anterior
# GRAFICA --------------------- import matplotlib.pyplot as plt titulo = 'Regla de Simpson 3/8' titulo = titulo + ', tramos:'+str(tramos) titulo = titulo + ', Area:'+str(suma) fx_existe = True try: # fx suave aumentando muestras muestrasfxSuave = tramos*10 + 1 xk = np.linspace(a,b,muestrasfxSuave) fk = fx(xk) except NameError: fx_existe = False try: # existen mensajes de error msj_existe = len(msj) except NameError: msj = [] # Simpson 3/8 relleno y bordes, cada 3 tramos for i in range(0,muestras-2,3): x_tramo = xi[i:(i+3)+1] f_tramo = fi[i:(i+3)+1] # interpolación polinomica a*(x**3)+b*(x**2)+c*x+d coef = np.polyfit(x_tramo, f_tramo, 3) # [a,b,c,d] px = lambda x: coef[0]*(x**3)+coef[1]*(x**2)+coef[2]*x+coef[3] xp = np.linspace(x_tramo[0],x_tramo[-1],21) fp = px(xp) plt.plot(xp,fp,linestyle='dashed',color='orange') relleno = 'lightgreen' if (i/3)%2==0: # bloque 3 tramos, es par relleno ='lightblue' plt.fill_between(xp,fp,fp*0,color=relleno) # Divisiones entre Simpson 3/8 for i in range(0,muestras,1): tipolinea = 'dotted' if i%3==0: # i es multiplo de 3 tipolinea = 'dashed' if len(msj)==0: # sin errores plt.vlines(xi[i],0,fi[i],linestyle=tipolinea, color='orange') # Graficar f(x), puntos if fx_existe==True: plt.plot(xk,fk,label='f(x)') plt.plot(xi,fi,'o',color='orange',label ='muestras') plt.xlabel('x') plt.ylabel('f(x)') plt.title(titulo) plt.legend() plt.tight_layout() plt.show()
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..
5. Algoritmo para x[i], f[i] como muestras en Python
Cuando se integra sobre muestras dadas por los vectores xi, fi. Se revisa que los tramos entre muestras sean iguales para un Simpson 3/8 y que existan suficientes puntos para completar el integral.
xi = [1. , 1.33333333, 1.66666667, 2. ,
2.33333333, 2.66666667, 3. ]
fi = [0.84147098, 1.12229722, 1.28506615, 1.28594075,
1.10453193, 0.74672307, 0.24442702]
Resultados con el algoritmo
tramos: 6 Integral fx con Simpson3/8: 2.0542043057079566
La gráfica se puede obtener usando el bloque correspondiente en la sección anterior.
# Integración Simpson 3/8 para muestras xi,fi import numpy as np # INGRESO xi = [1. , 1.33333333, 1.66666667, 2. , 2.33333333, 2.66666667, 3. ] fi = [0.84147098, 1.12229722, 1.28506615, 1.28594075, 1.10453193, 0.74672307, 0.24442702] # PROCEDIMIENTO casicero=1e-7 # decimales para truncar # vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) muestras = len(xi) tramos = muestras-1 msj = [] # mensajes de error if tramos<3: # puntos insuficientes msj.append(['tramos insuficientes:',tramos]) suma = 0 # integral numerico i = 0 while i<(muestras-3) and len(msj)==0: # i<tramos, al menos dos tramos h = xi[i+1]-xi[i] # tamaño de paso, supone constante if (i+2)<muestras: # dos tramos d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # 3 tramos equidistantes S38 = (3/8)*h*(fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]) suma = suma + S38 i = i+3 else: donde = np.argmax(np.abs(d2x))+i+1 msj.append(['no equidistantes en i',donde]) # SALIDA print('tramos: ',len(xi)-1) if len(msj)>0: # mensajes de error print('Revisar errores en xi:',xi) print('tramos:',np.diff(xi,1)) for unmsj in msj: print('',unmsj[0],':',unmsj[1]) else: print('Integral fx con Simpson3/8:',suma)
[ Simpson 3/8 ] [ Ejercicio ] [Algoritmo f(x) ] [ gráfica ] [ Algoritmo xi,fi ]
..