Ejercicio: 1Eva_2021PAOII_T2 Intersección de funciones – Obstrucción Radioenlace
Planteamiento del ejercicio
Para analizar la obstrucción se usan las expresiones del polinomio encontrado en el tema anterior y la función descrita en el enunciado. Se debe encontrar las distrancias en las que ambas expresiones son iguales, o también:
p(d)- f(d) = 0a. Establezca un intervalo de análisis para cada raíz.
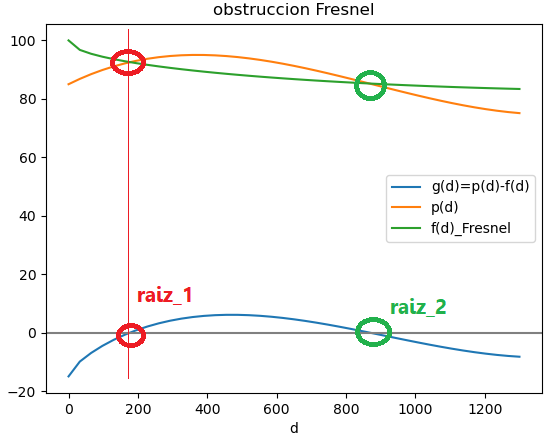
Según la gráfica presentada en el Tema 1 se tendrán que encontrar dos raíces:
[0,700] y [700,1300]
La expresión a usar en el ejercicio se obtiene como:
p_{3}(d) = 85.0+ 0.05941 d - 0.0001015 d^2 +3.842x10^{-8}d^3y para el radio de fresnel:
f(d) = h_{antena} - r r = \sqrt{\frac{n \lambda d_1 d_2}{d_1+d_2}} d_2 = d_{enlace} - d_1reemplazando los valores en las expresiones
f(d) = 100 - \sqrt{\frac{1 (0.3278 d_1 (3700-d_1}{3700}}La expresión para el ejercicio en el intervalo de obstrucción según la gráfica del tema 1 es:
g(d) = p(d)- f(d) = 0 g(d) = 85.0+ 0.05941 d - 0.0001015 d^2 +3.842x10^{-8}d^3 - - 100 - \sqrt{\frac{1 (0.3278 d_1 (3700-d_1}{3700}}Dado que es un ejercicio que se utiliza muchas veces en el análisis de radioenlaces, se utilizaría un algoritmo para aplicarlo en diferentes situaciones.
b. Realice al menos 3 iteraciones con el método de la Bisección para encontrar la primera raíz (izquierda)
a = 0, b = 700
con a = 0
g(0) = p(0)- f(0) = -15 p(0) = 85.0+ 0.05941 (0) - 0.0001015 (0)^2 +3.842x10^{-8}(0)^3 = 85 f(d) = 100 - \sqrt{\frac{1 (0.3278 d_1 (3700-d_1}{3700}} =100con b = 700
g(700) = p(700)- f(700) = 3.67 p(700) = 85.0+ 0.05941 (700) - 0.0001015 (700)^2 +3.842x10^{-8}(700)^3 f(700) = 100 - \sqrt{\frac{1 (0.3278 (700) (3700-(700)}{3700}}como hay cambio de signo entre g(a) y g(b), debe existir una raiz en el intervalo
iteración 1
c= \frac{a+b}{2} = \frac{700-0}{2} = 350 p(350) = 85.0+ 0.05941 (350) - 0.0001015 (350)^2 +3.842x10^{-8}(350)^3 f(350) = 100 - \sqrt{\frac{1 (0.3278 (350) (3700-(350}{3700}} g(350) = p(350)- f(350) = 5.199como la referencia es
g(0) = -15 g(700) = 3.67hay cambio de signo entre [0,350]
error estimado = 350-0 = 350
iteración 2
c= \frac{a+b}{2} = \frac{350-0}{2} = 175 p(175) = 85.0+ 0.05941 (175) - 0.0001015 (175)^2 +3.842x10^{-8}(175)^3 f(175) = 100 - \sqrt{\frac{1 (0.3278 (175) (3700-(175}{3700}} g(175) = -113.1como la referencia es
g(0) = -15 g(350) = 5.199hay cambio de signo entre [175,350]
error estimado = 350-175 = 175
iteración 3
Instrucciones en Python
resultado usando el algoritmo:
[ i, a, c, b, f(a), f(c), f(b), tramo]
1 0.000 350.000 700.000 -15.000 5.199 3.670 700.000
2 0.000 175.000 350.000 -15.000 -0.113 5.199 350.000
3 175.000 262.500 350.000 -0.113 3.237 5.199 175.000
4 175.000 218.750 262.500 -0.113 1.755 3.237 87.500
5 175.000 196.875 218.750 -0.113 0.872 1.755 43.750
6 175.000 185.938 196.875 -0.113 0.393 0.872 21.875
7 175.000 180.469 185.938 -0.113 0.143 0.393 10.938
8 175.000 177.734 180.469 -0.113 0.016 0.143 5.469
9 175.000 176.367 177.734 -0.113 -0.048 0.016 2.734
10 176.367 177.051 177.734 -0.048 -0.016 0.016 1.367
11 177.051 177.393 177.734 -0.016 -0.000 0.016 0.684
12 177.393 177.563 177.734 -0.000 0.008 0.016 0.342
13 177.393 177.478 177.563 -0.000 0.004 0.008 0.171
14 177.393 177.435 177.478 -0.000 0.002 0.004 0.085
15 177.393 177.414 177.435 -0.000 0.001 0.002 0.043
16 177.393 177.403 177.414 -0.000 0.000 0.001 0.021
17 177.393 177.398 177.403 -0.000 0.000 0.000 0.011
18 177.393 177.395 177.398 -0.000 -0.000 0.000 0.005
19 177.395 177.397 177.398 -0.000 0.000 0.000 0.003
20 177.395 177.396 177.397 -0.000 0.000 0.000 0.001
21 177.395 177.396 177.396 -0.000 0.000 0.000 0.001
raiz: 177.39558219909668
raiz en: 177.39558219909668
error en tramo: 0.000667572021484375
# Algoritmo de Bisección # [a,b] se escogen de la gráfica de la función # error = tolera import numpy as np import matplotlib.pyplot as plt # INGRESO p = lambda d: 85.0 + 0.05941*d - 0.0001015*d**2 +3.842e-8*d**3 f = lambda d: 100 - np.sqrt(1*(0.3278)*d*(3700-d)/3700) fx = lambda d: p(d)- f(d) a_todo = 0 b_todo = 1300 a = 0 b = 700 tolera = 0.001 muestras = 41 # PROCEDIMIENTO # PROCEDIMIENTO tabla = [] tramo = b-a fa = fx(a) fb = fx(b) i = 1 while (tramo>tolera): c = (a+b)/2 fc = fx(c) tabla.append([i,a,c,b,fa,fc,fb,tramo]) i = i + 1 cambia = np.sign(fa)*np.sign(fc) if (cambia<0): b = c fb = fc else: a=c fa = fc tramo = b-a c = (a+b)/2 fc = fx(c) tabla.append([i,a,c,b,fa,fc,fb,tramo]) tabla = np.array(tabla) raiz = c # SALIDA np.set_printoptions(precision = 4) print('[ i, a, c, b, f(a), f(c), f(b), tramo]') # print(tabla) # Tabla con formato n=len(tabla) for i in range(0,n,1): unafila = tabla[i] formato = '{:.0f}'+' '+(len(unafila)-1)*'{:.3f} ' unafila = formato.format(*unafila) print(unafila) print('raiz: ',raiz) print(' raiz en: ', c) print('error en tramo: ', tramo) # GRAFICA xi = np.linspace(a_todo,b_todo,muestras) yi = fx(xi) pi = p(xi) ri = f(xi) plt.plot(xi,yi,label='g(d)=p(d)-f(d)') plt.plot(xi,pi,label='p(d)') plt.plot(xi,ri,label='f(d)_Fresnel') plt.axhline(0, color='grey') plt.xlabel('d') plt.legend() plt.title('obstruccion Fresnel') plt.show()
c. Desarrolle al menos 3 iteraciones con el método del Punto fijo para encontrar el segundo punto (derecha)
La siguiente raíz se encuentra con algoritmo presentado o también con el algoritmo del siguiente literal usando la misma expresion g(d).
a = 700 b= 1300
raiz en: 867.1000480651855 error en tramo: 0.00057220458984375