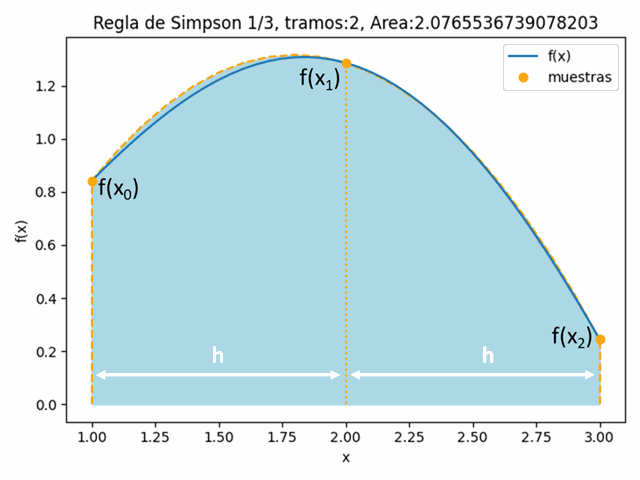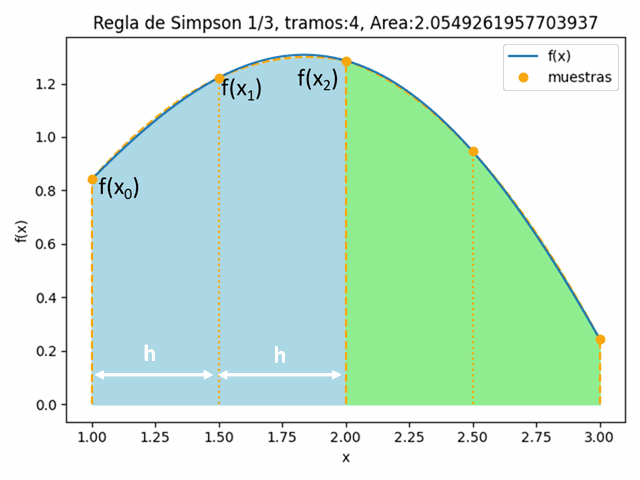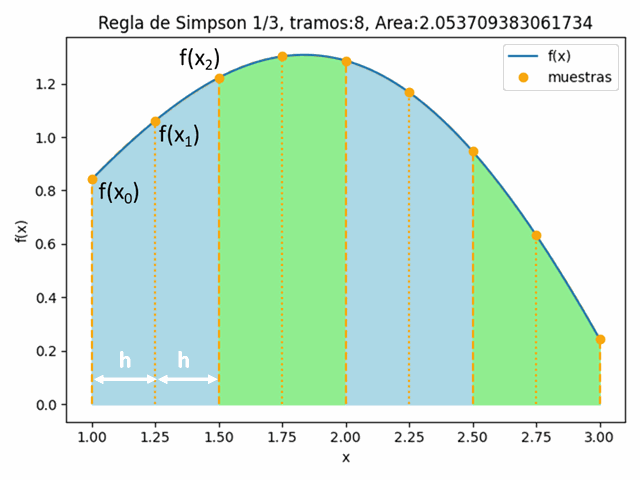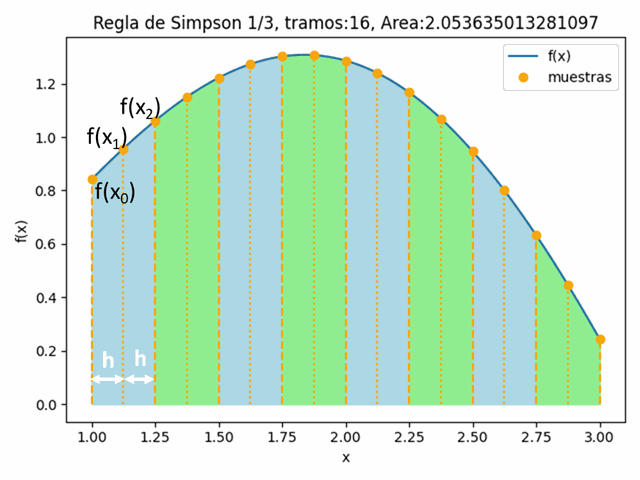
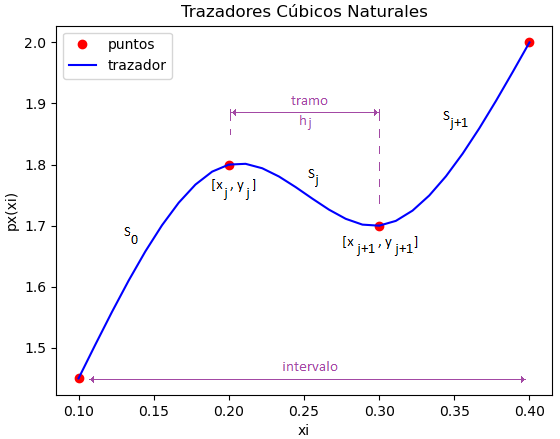
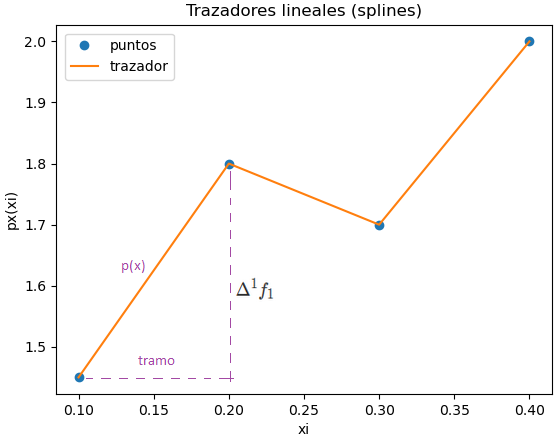
[ Dif_Finitas ] [ Dif_Finitas avanzadas ] [ Dif_Divididas_Newton ]
Solo para fines didácticos, y como complemento para los ejercicios presentados en la unidad para Interpolación polinómica, se presentan las instrucciones para las animaciones usadas en la presentación de los conceptos y ejercicios. Los algoritmos para animación NO son necesarios para realizar los ejercicios, que requieren una parte analítica con al menos tres iteraciones en papel y lápiz. Se lo adjunta como una herramienta didáctica de asistencia para las clases.
En los algoritmos, se convierten las partes en funciones, que se usan para generar los polinomios para cada grado y se incorporan en un gráfico animado con los resultados presentados.
Para la gráfica animada se añaden las instrucciones siguientes:
Se determina el intervalo para el eje x usando los valores mínimos y máximos del vector xi. Se toma como muestras para el polinomio las suficientes para una línea suave, que pueden ser mayores a 21 y se crean los valores para el polinomio en p_xi.
Para cada polinomio se guarda en una tabla los valores px(p_xi)del polinomio evaluado el vector p_xi
La gráfica (graf_ani) se crea en una ventana (fig_ani), inicializando con los puntos [xi,fi] en color rojo, y configurando los parámetros base para el gráfico.
Se usan procedimientos para crear unatrama() para cada polinomio y en cada cambio se limpia la trama manteniendo la base con limpiatrama().
En caso de requerir un archivo gif animado se proporciona un nombre de archivo. Para crear el archivo se requiere de la librería 'pillow'.
otros ejemplos de animación en el curso de Fundamentos de Programación:
Movimiento circular – Una partícula, animación con matplotlib-Python
Interpolación por Diferencias Finitas Avanzadas
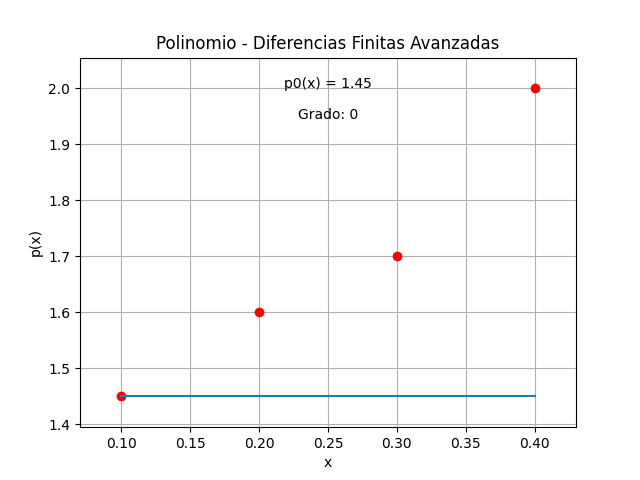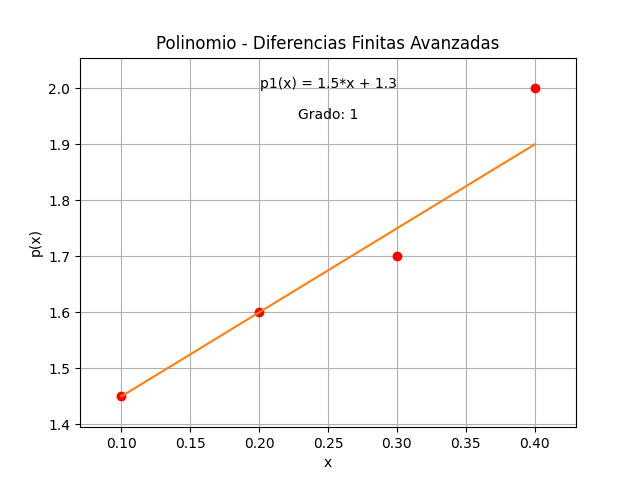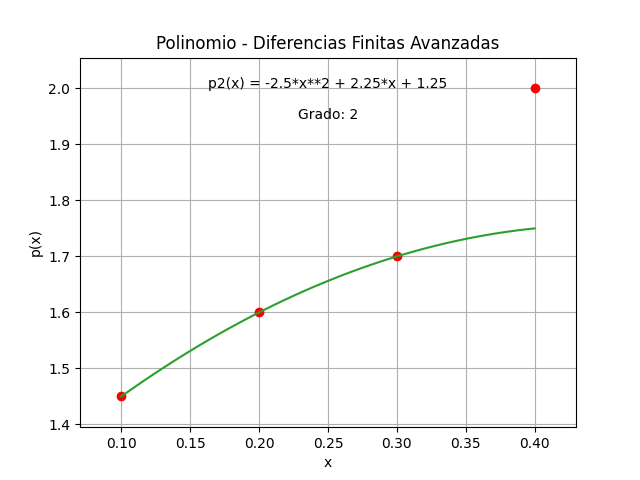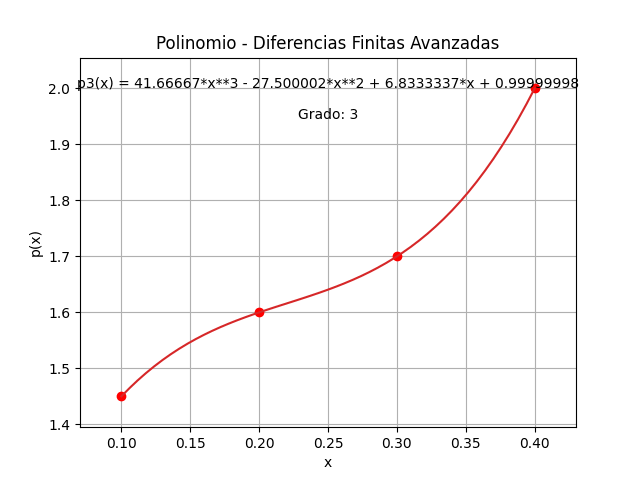
En la función para interpolación se añade la verificación de tamaños de paso equidistantes o iguales. En el caso de no tener tamaños de paso equidistantes
tabla de diferencias finitas
['i', 'xi', 'fi', 'd1f', 'd2f']
[[0. 0.1 1.45 0.15 0. ]
[1. 0.2 1.6 0. 0. ]]
dfinita: [0.15 0. ]
1.45 +
+( 0.15 / 0.1 )* ( x - 0.1 )
polinomio simplificado
1.5*x + 1.3
tabla de diferencias finitas
['i', 'xi', 'fi', 'd1f', 'd2f', 'd3f']
[[ 0. 0.1 1.45 0.15 -0.05 0. ]
[ 1. 0.2 1.6 0.1 0. 0. ]
[ 2. 0.3 1.7 0. 0. 0. ]]
dfinita: [ 0.15 -0.05 0. ]
1.45 +
+( 0.15 / 0.1 )* ( x - 0.1 )
+( -0.05 / 0.02 )* (x - 0.2)*(x - 0.1)
polinomio simplificado
-2.5*x**2 + 2.25*x + 1.25
tabla de diferencias finitas
['i', 'xi', 'fi', 'd1f', 'd2f', 'd3f', 'd4f']
[[ 0. 0.1 1.45 0.15 -0.05 0.25 0. ]
[ 1. 0.2 1.6 0.1 0.2 0. 0. ]
[ 2. 0.3 1.7 0.3 0. 0. 0. ]
[ 3. 0.4 2. 0. 0. 0. 0. ]]
dfinita: [ 0.15 -0.05 0.25 0. ]
1.45 +
+( 0.15 / 0.1 )* ( x - 0.1 )
+( -0.05 / 0.02 )* (x - 0.2)*(x - 0.1)
+( 0.25 / 0.006 )* (x - 0.3)*(x - 0.2)*(x - 0.1)
polinomio simplificado
41.66667*x**3 - 27.500002*x**2 + 6.8333337*x + 0.99999998
Polinomios con Diferencias Finitas Avanzadas
px_0 =
1.45
px_1 =
1.5*x + 1.3
px_2 =
2
- 2.5*x + 2.25*x + 1.25
px_3 =
3 2
41.66667*x - 27.500002*x + 6.8333337*x + 0.99999998
El resumen de las instrucciones se presentan a continuación.
# Interpolación -Diferencias finitas avanzadas
# Tarea: Verificar tamaño de vectores,
# verificar puntos equidistantes en x
import numpy as np
import math
import sympy as sym
def dif_finitas(xi,fi, precision=5, vertabla=False):
'''Genera la tabla de diferencias finitas
resultado en: tabla,titulo
Tarea: verificar tamaño de vectores
'''
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
# Tabla de Diferencias Finitas
titulo = ['i','xi','fi']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)
# diferencias finitas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)
# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
# Añade título para cada columna
titulo.append('d'+str(j-2)+'f')
# cada fila de columna
i = 0
while (i < diagonal):
tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1]
i = i+1
diagonal = diagonal - 1
j = j+1
if vertabla==True:
np.set_printoptions(precision)
print('tabla de diferencias finitas')
print(titulo)
print(tabla)
return(tabla, titulo)
def pasosEquidistantes(xi, casicero = 1e-15):
''' Revisa tamaños de paso h en vector xi.
True: h son equidistantes,
False: h tiene tamaño de paso diferentes y dónde.
'''
xi = np.array(xi,dtype=float)
n = len(xi)
# revisa tamaños de paso equidistantes
h_iguales = True
if n>3:
dx = np.zeros(n,dtype=float)
for i in range(0,n-1,1): # calcula hi como dx
dx[i] = xi[i+1]-xi[i]
for i in range(0,n-2,1): # revisa diferencias
dx[i] = dx[i+1]-dx[i]
if dx[i]<=casicero: # redondea cero
dx[i]=0
if abs(dx[i])>0:
h_iguales=False
print('tamaños de paso diferentes en i:',i+1,',',i+2)
dx[n-2]=0
return(h_iguales)
def interpola_dfinitasAvz(xi,fi, vertabla=False,
precision=5, casicero = 1e-15):
'''Interpolación de diferencias finitas
resultado: polinomio en forma simbólica,
redondear a cero si es menor que casicero
'''
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
n = len(xi)
# revisa tamaños de paso equidistantes
h_iguales = pasosEquidistantes(xi, casicero)
if vertabla==True:
np.set_printoptions(precision)
# POLINOMIO con diferencias Finitas avanzadas
x = sym.Symbol('x')
polisimple = sym.S.NaN # expresión del polinomio con Sympy
if h_iguales==True:
tabla,titulo = dif_finitas(xi,fi,vertabla)
h = xi[1] - xi[0]
dfinita = tabla[0,3:]
if vertabla==True:
print('dfinita: ',dfinita)
print(fi[0],'+')
n = len(dfinita)
polinomio = fi[0]
for j in range(1,n,1):
denominador = math.factorial(j)*(h**j)
factor = np.around(dfinita[j-1]/denominador,precision)
termino = 1
for k in range(0,j,1):
termino = termino*(x-xi[k])
if vertabla==True:
txt1='';txt2=''
if n<=2 or j<=1:
txt1 = '('; txt2 = ')'
print('+(',np.around(dfinita[j-1],precision),
'/',np.around(denominador,precision),
')*',txt1,termino,txt2)
polinomio = polinomio + termino*factor
# simplifica multiplicando entre (x-xi)
polisimple = polinomio.expand()
if vertabla==True:
print('polinomio simplificado')
print(polisimple)
return(polisimple)
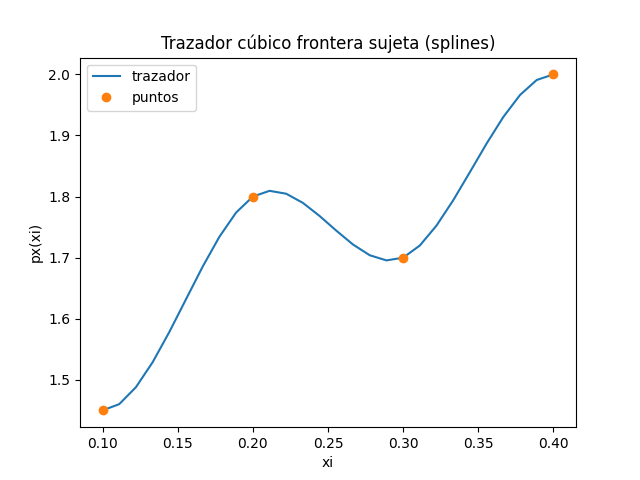
# INGRESO , Datos de prueba
xi = [0.10, 0.2, 0.3, 0.4]
fi = [1.45, 1.6, 1.7, 2.0]
# PROCEDIMIENTO
# tabla polinomios
n = len(xi)
px_tabla = [fi[0]]
for grado in range(1,n,1):
polinomio = interpola_dfinitasAvz(xi[:grado+1],fi[:grado+1],
vertabla=True, precision=4)
print('',)
px_tabla.append(polinomio)
# SALIDA
print('Polinomios con Diferencias Finitas Avanzadas')
for grado in range(0,n,1):
print('px_'+str(grado)+' =') #, px_tabla[grado])
sym.pprint(px_tabla[grado])
print()
Parte adicional para la gráfica con GIF animado
# GRAFICA CON ANIMACION polinomios --------
import matplotlib.pyplot as plt
import matplotlib.animation as animation
unmetodo = 'Diferencias Finitas Avanzadas'
narchivo = 'DifFinitasAvz' # nombre archivo
muestras = 51 # de cada p(X)
# Puntos para la gráfica
a = np.min(xi)
b = np.max(xi)
p_xi = np.linspace(a,b,muestras)
# lineas por grado de polinomio
x = sym.Symbol('x')
px_lineas = np.zeros(shape=(n,muestras), dtype=float)
for grado in range(0,n,1):
polinomio = px_tabla[grado]
px = sym.utilities.lambdify(x,polinomio,'numpy')
px_lineas[grado] = px(p_xi)
# Parametros de trama/foto
retardo = 800 # milisegundos entre tramas
tramas = len(px_lineas)
ymax = np.max(fi)
ymin = np.min(fi)
deltax = 0.1*np.abs(b-a)
deltay = 0.1*np.abs(ymax-ymin)
# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
# Función Base
fx_linea, = graf_ani.plot(xi,fi,'o',color='red')
# Polinomios de px_tabla grado = 0
px_unalinea, = graf_ani.plot(p_xi, px_lineas[0],
label='grado: 0')
# Configura gráfica
graf_ani.set_xlim([a-deltax,b+deltax])
graf_ani.set_ylim([ymin-deltay,ymax+deltay])
graf_ani.axhline(0, color='k') # Linea horizontal en cero
graf_ani.set_title('Polinomio - '+unmetodo)
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('p(x)')
graf_ani.grid()
# Cuadros de texto en gráfico
txt_x = (b+a)/2
txt_y = ymax
txt_poli = graf_ani.text(txt_x, txt_y,'p(x):',
horizontalalignment='center')
txt_grado = graf_ani.text(txt_x, txt_y-deltay,'grado:',
horizontalalignment='center')
# Nueva Trama
def unatrama(i,p_xi,pxi):
# actualiza cada linea
px_unalinea.set_xdata(p_xi)
px_unalinea.set_ydata(pxi[i])
unpolinomio = px_tabla[i]
if unpolinomio == sym.S.NaN:
unpolinomio = 'h pasos no equidistantes'
etiquetap = 'p'+str(i)+'(x) = '+str(unpolinomio)
px_unalinea.set_label(etiquetap)
# actualiza texto
txt_poli.set_text(etiquetap)
txt_grado.set_text('Grado: '+str(i))
# color de la línea
if (i<=9):
lineacolor = 'C'+str(i)
else:
numerocolor = i%10
lineacolor = 'C'+str(numerocolor)
px_unalinea.set_color(lineacolor)
return (px_unalinea, txt_poli, txt_grado)
# Limpia Trama anterior
def limpiatrama():
px_unalinea.set_ydata(np.ma.array(p_xi, mask=True))
px_unalinea.set_label('')
txt_poli.set_text('')
txt_grado.set_text('')
return (px_unalinea,txt_poli, txt_grado)
# Trama contador
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(fig_ani,
unatrama,
i ,
fargs = (p_xi,px_lineas),
init_func = limpiatrama,
interval = retardo,
blit=True)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_GIFanimado.gif', writer='pillow')
# ani.save(narchivo+'_video.mp4')
plt.draw()
plt.show()
[ Dif_Finitas ] [ Dif_Finitas avanzadas ] [ Dif_Divididas_Newton ]
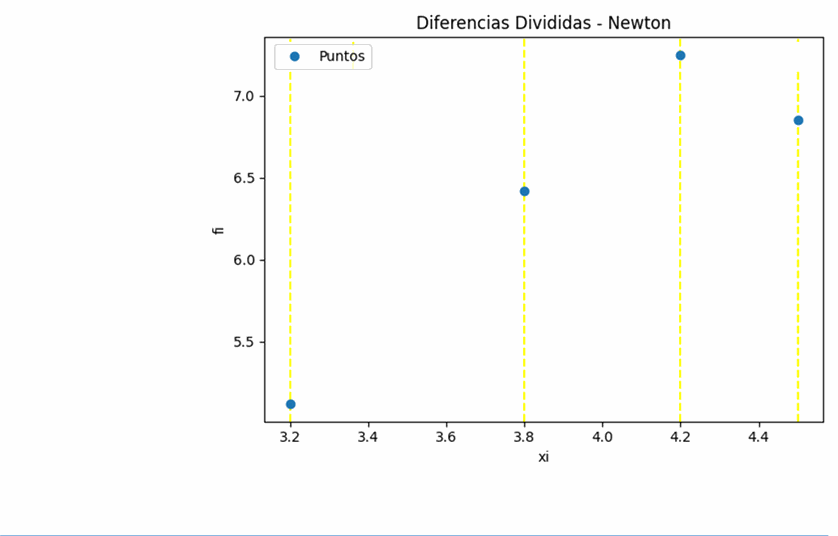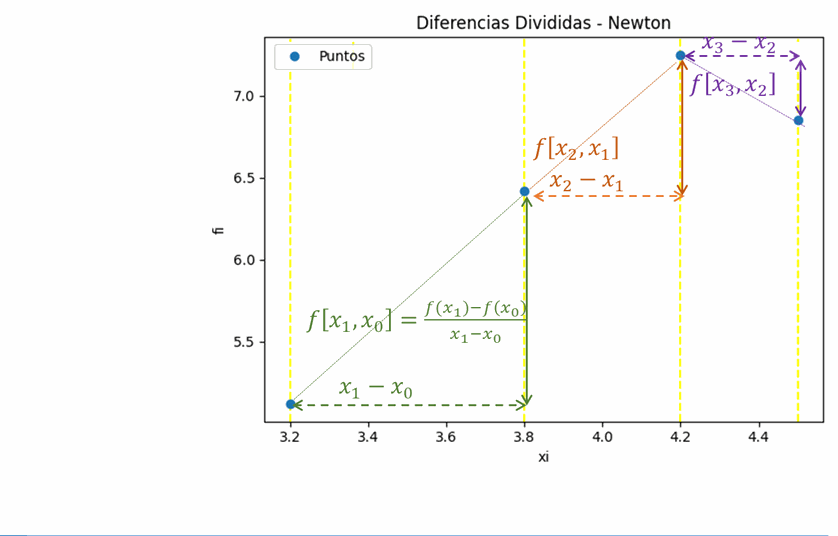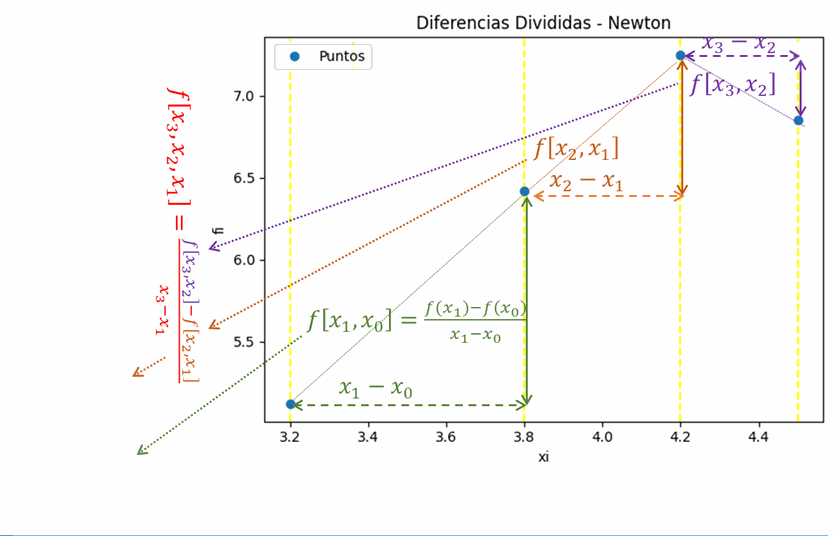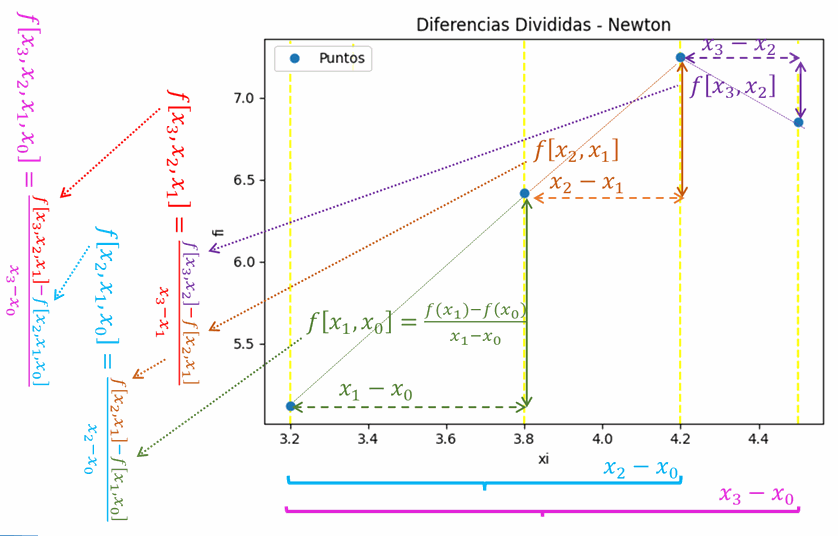
Interpolación por Diferencias Divididas de Newton
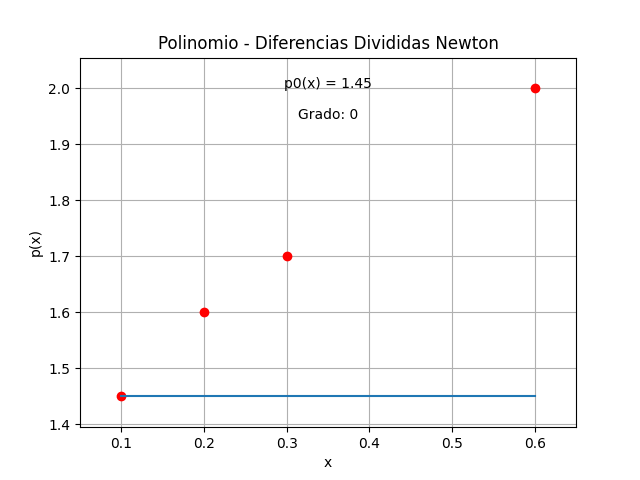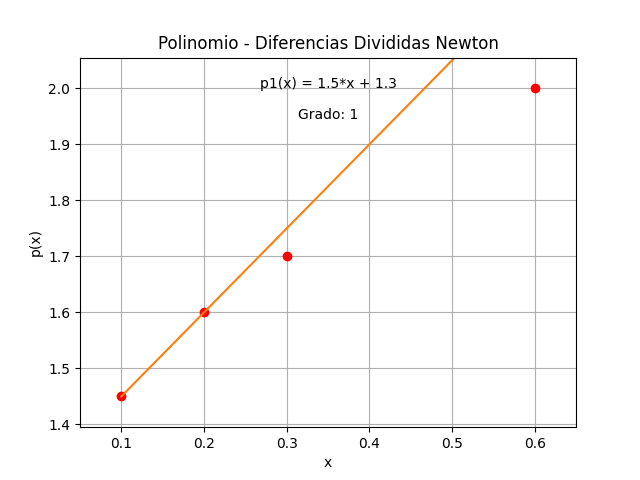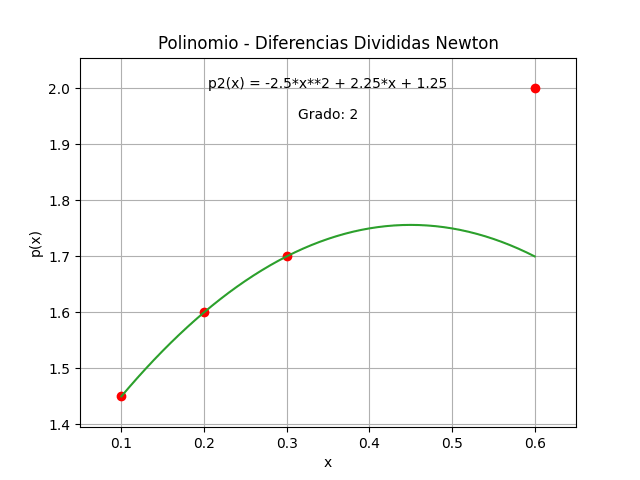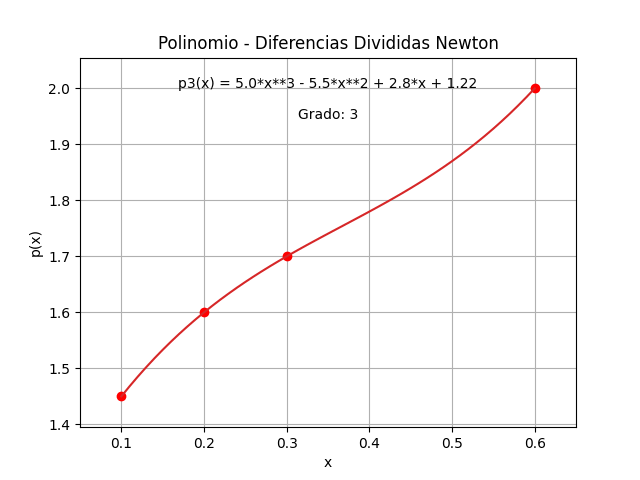
tabla de diferencias divididas
['i', 'xi', 'fi', 'F[1]', 'F[2]']
[[0. 0.1 1.45 1.5 0. ]
[1. 0.2 1.6 0. 0. ]]
difDividida: [1.5 0. ]
1.45 +
+( 1.5 )*( x - 0.1 )
polinomio simplificado
1.5*x + 1.3
tabla de diferencias divididas
['i', 'xi', 'fi', 'F[1]', 'F[2]', 'F[3]']
[[ 0. 0.1 1.45 1.5 -2.5 0. ]
[ 1. 0.2 1.6 1. 0. 0. ]
[ 2. 0.3 1.7 0. 0. 0. ]]
difDividida: [ 1.5 -2.5 0. ]
1.45 +
+( 1.5 )*( x - 0.1 )
+( -2.5 )* (x - 0.2)*(x - 0.1)
polinomio simplificado
-2.5*x**2 + 2.25*x + 1.25
tabla de diferencias divididas
['i', 'xi', 'fi', 'F[1]', 'F[2]', 'F[3]', 'F[4]']
[[ 0.00000e+00 1.00000e-01 1.45000e+00 1.50000e+00 -2.50000e+00
5.00000e+00 0.00000e+00]
[ 1.00000e+00 2.00000e-01 1.60000e+00 1.00000e+00 3.33067e-15
0.00000e+00 0.00000e+00]
[ 2.00000e+00 3.00000e-01 1.70000e+00 1.00000e+00 0.00000e+00
0.00000e+00 0.00000e+00]
[ 3.00000e+00 6.00000e-01 2.00000e+00 0.00000e+00 0.00000e+00
0.00000e+00 0.00000e+00]]
difDividida: [ 1.5 -2.5 5. 0. ]
1.45 +
+( 1.5 )*( x - 0.1 )
+( -2.5 )* (x - 0.2)*(x - 0.1)
+( 5.0 )* (x - 0.3)*(x - 0.2)*(x - 0.1)
polinomio simplificado
5.0*x**3 - 5.5*x**2 + 2.8*x + 1.22
Polinomios con Diferencias Divididas Newton
px_0 =
1.45
px_1 =
1.5*x + 1.3
px_2 =
2
- 2.5*x + 2.25*x + 1.25
px_3 =
3 2
5.0*x - 5.5*x + 2.8*x + 1.22
>>>
Instrucciones en Python
# Interpolación -Diferencias Divididas de Newton
# Tarea: Verificar tamaño de vectores,
import numpy as np
import sympy as sym
def dif_divididas(xi,fi, vertabla=False,
precision=5, casicero = 1e-15):
'''Genera la tabla de diferencias divididas
resultado en: tabla, titulo
Tarea: verificar tamaño de vectores
'''
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
# Tabla de Diferencias Divididas
titulo = ['i','xi','fi']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)
# diferencias divididas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)
# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
# Añade título para cada columna
titulo.append('F['+str(j-2)+']')
# cada fila de columna
i = 0
paso = j-2 # inicia en 1
while (i < diagonal):
denominador = (xi[i+paso]-xi[i])
numerador = tabla[i+1,j-1]-tabla[i,j-1]
tabla[i,j] = numerador/denominador
if np.abs(tabla[i,j])<= casicero:
tabla[i,j] = 0
i = i+1
diagonal = diagonal - 1
j = j+1
if vertabla==True:
np.set_printoptions(precision)
print('tabla de diferencias divididas')
print(titulo)
print(tabla)
return(tabla, titulo)
def interpola_difDividida(xi,fi, vertabla=False,
precision=5, casicero = 1e-15):
'''Interpolación de diferencias finitas
resultado: polinomio en forma simbólica,
redondear a cero si es menor que casicero
'''
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
# Tabla de Diferencias Divididas
tabla,titulo = dif_divididas(xi,fi,vertabla,
precision,casicero)
dDividida = tabla[0,3:]
n = len(dDividida)
x = sym.Symbol('x')
polinomio = fi[0]
if vertabla==True:
print('difDividida: ',dDividida)
print(fi[0],'+')
for j in range(1,n,1):
factor = np.around(dDividida[j-1],precision)
termino = 1
for k in range(0,j,1):
termino = termino*(x-xi[k])
if vertabla==True:
txt1='';txt2=''
if n<=2 or j<=1:
txt1 = '('; txt2 = ')'
print('+(',factor,')*'+txt1,termino,txt2)
polinomio = polinomio + termino*factor
# simplifica multiplicando entre (x-xi)
polisimple = polinomio.expand()
if vertabla==True:
print('polinomio simplificado')
print(polisimple)
return(polisimple)
# INGRESO , Datos de prueba
xi = [0.10, 0.2, 0.3, 0.6]
fi = [1.45, 1.6, 1.7, 2.0]
# PROCEDIMIENTO
# tabla polinomios
n = len(xi)
px_tabla = [fi[0]]
for grado in range(1,n,1):
polinomio = interpola_difDividida(xi[:grado+1],fi[:grado+1],
vertabla=True)
print('',)
px_tabla.append(polinomio)
# SALIDA
print('Polinomios con Diferencias Divididas Newton')
for grado in range(0,n,1):
print('px_'+str(grado)+' =') #, px_tabla[grado])
sym.pprint(px_tabla[grado])
print()
Para la gráfica animada se usa el mismo bloque de instrucciones del método de Diferencias Finitas avanzadas, solo requiere cambiar el nombre del método y el nombre para el archivo GIF animado.
Interpolación por el Método de Lagrange
Interpola con Lagrange
1.45 * (x - 0.4)*(x - 0.3)*(x - 0.2) / (-0.2 + 0.1)*(-0.3 + 0.1)*(-0.4 + 0.1)
+ 1.6 * (x - 0.4)*(x - 0.3)*(x - 0.1) / (-0.1 + 0.2)*(-0.3 + 0.2)*(-0.4 + 0.2)
+ 1.7 * (x - 0.4)*(x - 0.2)*(x - 0.1) / (-0.1 + 0.3)*(-0.2 + 0.3)*(-0.4 + 0.3)
+ 2.0 * (x - 0.3)*(x - 0.2)*(x - 0.1) / (-0.1 + 0.4)*(-0.2 + 0.4)*(-0.3 + 0.4)
polinomio simplificado
41.666667*x**3 - 27.5*x**2 + 6.833333*x + 1.0
Interpolación con Lagrange
41.666667*x**3 - 27.5*x**2 + 6.833333*x + 1.0
>>>
Instrucciones en Python
# Interpolación - Lagrange
# Tarea: Verificar tamaño de vectores,
import numpy as np
import sympy as sym
def interpola_Lagrange(xi,fi,vertabla=False,
precision=6, casicero = 1e-15):
'''
Interpolación con método de Lagrange
resultado: polinomio en forma simbólica
'''
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
n = len(xi)
x = sym.Symbol('x')
# Polinomio con Lagrange
if vertabla==True:
print('Interpola con Lagrange')
polinomio = sym.S.Zero
for i in range(0,n,1):
# Termino de Lagrange
termino = 1
numerador = 1
denominador = 1
for j in range(0,n,1):
if (j!=i):
numerador = numerador*(x-xi[j])
denominador = denominador*(sym.UnevaluatedExpr(xi[i])-xi[j])
if vertabla==True:
txt0='' ; txt1='('; txt2=')'
if i>0:
txt0='+'
if n>2:
txt1=''; txt2=''
print(txt0,fi[i],'*'+txt1,numerador,txt2+'/'+ txt1,
denominador,txt2)
#factor = np.around(fi[i]/float(denominador.doit()),precision)
polinomio = polinomio + (fi[i]/denominador.doit())*numerador
# Expande el polinomio
polisimple = polinomio.expand()
polisimple = redondea_coef(polisimple, precision)
if vertabla==True:
print('polinomio simplificado')
print(polisimple)
return(polisimple)
def redondea_coef(ecuacion, precision=6,casicero = 1e-15):
''' redondea coeficientes de términos suma de una ecuacion
'''
tipo = type(ecuacion)
tipo_eq = False
if tipo == sym.core.relational.Equality:
RHS = ecuacion.rhs
ecuacion = ecuacion.lhs
tipo = type(ecuacion)
tipo_eq = True
if tipo == sym.core.add.Add: # términos suma de ecuacion
term_sum = sym.Add.make_args(ecuacion)
ecuacion = sym.S.Zero
for term_k in term_sum:
# factor multiplicativo de termino suma
term_mul = sym.Mul.make_args(term_k)
producto = sym.S.One
for factor in term_mul:
if not(factor.has(sym.Symbol)):
factor = np.around(float(factor),precision)
if (abs(factor)%1)<casicero: # si es entero
factor = int(factor)
producto = producto*factor
ecuacion = ecuacion + producto
if tipo == sym.core.mul.Mul: # termino único, busca factores
term_mul = sym.Mul.make_args(ecuacion)
producto = sym.S.One
for factor in term_mul:
if not(factor.has(sym.Symbol)):
factor = np.around(float(factor),precision)
print(factor)
if (abs(factor)%1)<casicero: # si es entero
factor = int(factor)
producto = producto*factor
ecuacion = producto
if tipo == float: # si es entero
if (abs(ecuacion)%1)<casicero:
ecuacion = int(ecuacion)
if tipo_eq:
ecuacion = sym.Eq(ecuacion,RHS)
return(ecuacion)
# INGRESO , Datos de prueba
xi = [0.10, 0.2, 0.3, 0.4]
fi = [1.45, 1.6, 1.7, 2.0]
# PROCEDIMIENTO
# tabla polinomios
polisimple = interpola_Lagrange(xi,fi,
vertabla=True)
# SALIDA
print('Interpolación con Lagrange')
print(polisimple)
Para la gráfica animada se usa el mismo bloque de instrucciones del método de Diferencias Finitas avanzadas, solo requiere cambiar el nombre del método y el nombre para el archivo GIF animado.
 Instrucciones en Python adicionales al algoritmo anterior
Instrucciones en Python adicionales al algoritmo anterior