Sean B_1=\{ p(x),q(x),r(x) \} y B_2=\{s(x),t(x),u(x)\} dos bases ordenadas de \mathbb{P}_2. Si se conoce que:\begin{aligned}[x^2-x]_{B_1} &= (1,1,0)\\ {[x+1]_{B_1}}&=(0,1,0) \\ {[2x^2+1]_{B_1}}&=(1,-1,1) \\ {[s(x)+t(x)]_{B_1}}&=(1,1,0) \\{[t(x)+u(x)]_{B_1}}&=(5,2,0) \\{[u(x)]_{B_1}}&=(3,0,0) \end{aligned}Determine los vectores de cada base.
En el espacio vectorial de \mathbb{P}_3 se definen los siguientes subespacios vectoriales\begin{aligned} H&=gen\{ 2x^3+x^2,x+1 \} \\ W&=gen\{ 2-x,3+3x \} \end{aligned}Determine H\cap W y H+W junto con sus respectivas bases y dimensiones.
Sea V el espacio vectorial de \mathbb{P}_2 con producto interno\langle p,q \rangle=p(-1)q(-1)+p(0)q(0)+p(1)q(1)Considere el subespacio vectorial de V definido comoW=\{ p(x)\in\mathbb{P}_2\; ; \; p'(-1)=p'(1) \}Escriba el vector p(x)=x^2+2x como la suma de dos vectores de V, uno de W y otro de W^{\perp}.
Sea T una transformación lineal definida como T:\mathbb{R}^2\longrightarrow\mathbb{R}^3 con reglas de correspondenciaT\begin{pmatrix} a\\b \end{pmatrix}=\begin{pmatrix} \begin{aligned} a&+2b\\a&+b\\a&-b \end{aligned} \end{pmatrix}
a. Encuentre una base y dimensión del núcleo y recorrido de T.
b. Halle la matriz asociada a T con respecto a las bases B=\{ (1,-1),(2,1) \} de \mathbb{R}^2 y B'=\{ (1,1,0),(1,0,1),(0,1,1) \} de \mathbb{R}^3.
Una empresa produce tres productos, los mismos que se procesan en tres máquinas. El tiempo en horas requerido para procesar una unidad de cada producto por las tres máquinas se da a continuación:
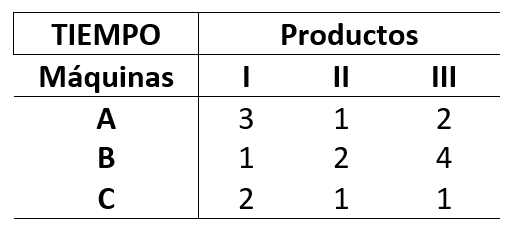
Se dispone de la máquina A por 850 horas, de la máquina B por 1200 horas y de la máquina C por 550 horas. ¿Cuántas unidades de cada producto deberían producirse con objeto de emplear todo el tiempo disponible de las máquinas?
