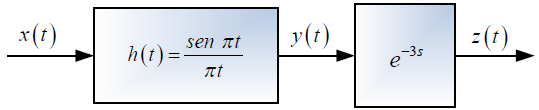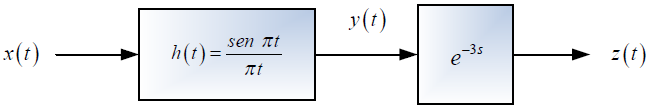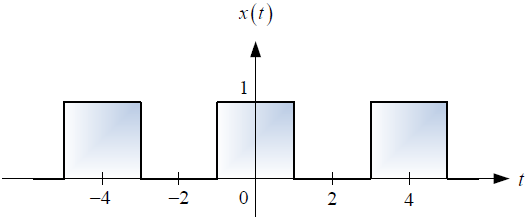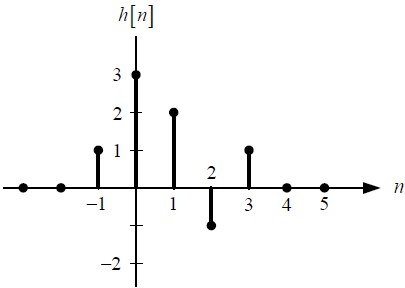3ra Evaluación II Término 2011-2012. 16/Febrero/2012. TELG1001
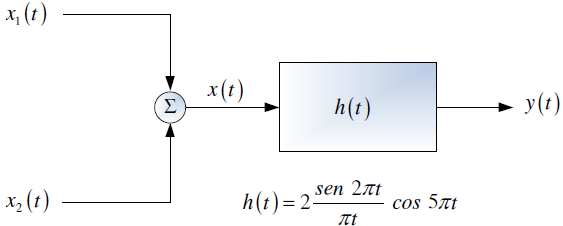
Tema 1. (40 puntos) Un estudiante de la materia Sistemas Lineales ha encontrado que la respuesta impulso h(t), de un sistema LTI-CT, es aquella que se especifica en la siguiente figura.
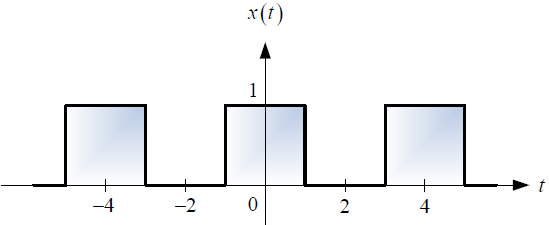
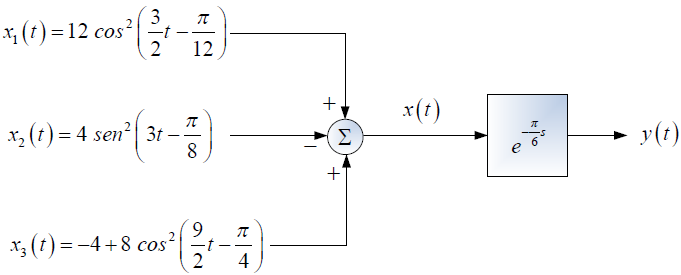
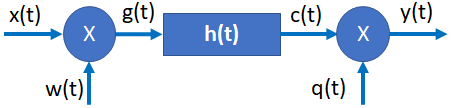
Si el referido sistema es excitado con la señal cuadrada periódica x(t), determinar, esquematizar y etiquetar según corresponda, lo siguiente:
a. La respuesta de frecuencia H(ω) vs ω.
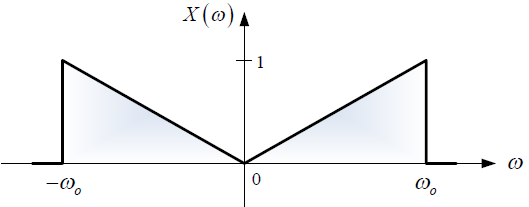
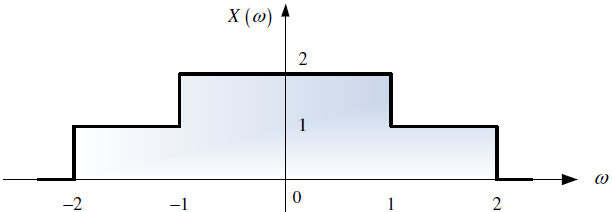
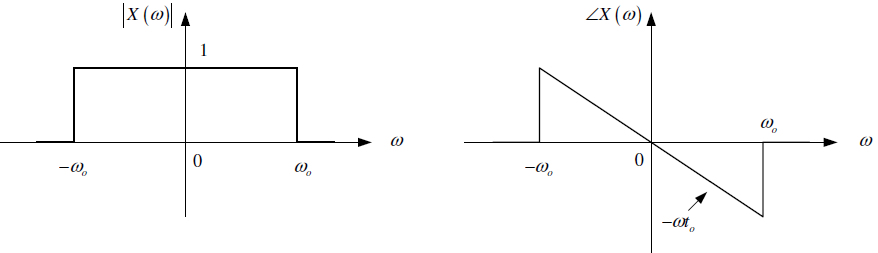
b. La respuesta de frecuencia X(ω) vs ω.
c. La respuesta de frecuencia Y(ω) vs ω y Z(ω) vs ω.
d. La expresión analítica de la salida y(t).
Coordinador: Tama Alberto