[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
..
Cuadratura con dos puntos – Experimento
Para visualizar el concepto de Cuadratura de Gauss de dos puntos considere lo siguiente:
Se tiene un corte transversal del un recipiente rectangular lleno de líquido limitado en x entre [-1,1], al que se le ha depositado encima otro recipiente con perfil f(x) = x2 hasta que reposan sus extremos en x[-1,1].
La altura de ambos recipientes es la misma.
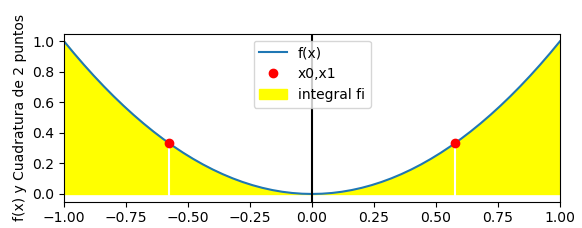
La superficie entre f(x) y el eje x es el integral de f(x) en el intervalo.
Si suponemos que la figura es el corte transversal de una vasija y la parte en amarillo es líquida, la vasija ha desplazado el líquido que ocupa ahora el «área» mostrada en la gráfica que corresponde al integral de f(x)=x2. entre [-1,1].
Ahora, suponga que se perfora el perfil de f(x) en dos puntos equidistantes cercanos x=0. Los orificios permitirían el desplazamiento del liquido al interior de f(x) que dejando pasar suficiente tiempo, permitiría tener todo el líquido en el recipiente rectangular entre [-1,1] como una línea horizontal.
Podría medir la altura que tiene el líquido y que tiene un equivalente en un punto f(x1). Debería encontrar el valor de x1 que permite disponer del mismo valor entre el área debajo de f(x) y el rectángulo del corte transversal amarillo ahora formado.
Se usa el resultado analítico del integral restando el área del rectángulo obtenido al evaluar la función f(x) entre [0,1], teniendo un problema de búsqueda de raíces. Obtenemos el valor de x1.
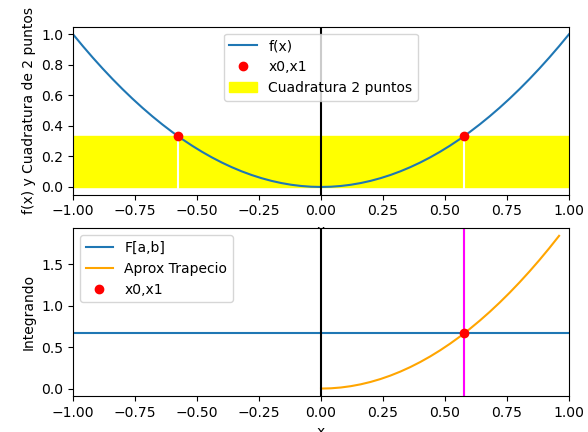
Se muestra que el área bajo f(x) es equivalente al área del rectángulo conformado.
Si utilizamos el desplazamiento horizontal desde el centro para un punto encontrado como un «factor», tendremos que el área del rectángulo se mantendría equivalente, y el desplazamiento proporcional a la mitad del intervalo si se varía el intervalo de observación. Este factor coincide con el factor de Cuadratura de Gauss de dos puntos.
funcion fx: x**2 Integral Fx: x**3/3 I analitico: 0.6666666666666666 I aproximado: 0.6666666666654123 desplaza centro: 0.5773502691890826 factor desplaza: 0.5773502691890826 Factor CuadGauss: 0.5773502691896258 erradoFactor: 1.2545520178264269e-12 error integral: 1.2543299732215019e-12
El error del integral es del orden de 10-12
Cambiamos la figura geométrica a un trapecio generado por la recta que pasa por los puntos xi desplazados desde el centro.
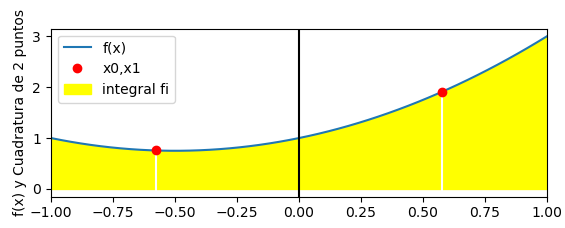
Usamos la función f(x) = x2 + x + 1, observaremos si los resultado son equivalentes.
La figura al inicio del experimento será:
Luego de realizar realizar el mismo cálculo anterior usando un equivalente a trapecio se tiene:
con valores numéricos:
funcion fx: x**2 + x + 1 Integral Fx: x**3/3 + x**2/2 + x I analitico: 2.6666666666666665 I aproximado: 2.6666666666654124 desplaza centro: 0.5773502691890826 factor desplaza: 0.5773502691890826 Factor CuadGauss: 0.5773502691896258 erradoFactor: 1.2545520178264269e-12 error integral: 1.2541079286165768e-12
El error del integral es también del orden de 10-12, además observe que el factor de cuadratura de Gauss se mantiene.
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
Tarea
Realice el experimento usando un polinomio de grado superior y observe los errores para el integral y las diferencia con el coeficiente de Cuadratura de 2 puntos.
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]
Algoritmo con Python
Para resumir la cantidad de instrucciones, se usa el método de la bisección desde la librería Scipy y el subgrupo de funciones de optimización.
Los cálculos para realizar las gráficas se tratan en un bloque luego de mostrar los resultado principales.
# Integración: Cuadratura de Gauss de dos puntos # modelo con varios tramos entre [a,b] # para un solo segmento. import numpy as np import matplotlib.pyplot as plt import sympy as sym import scipy.optimize as op # INGRESO x = sym.Symbol('x') # fx = (x)**2 fx = x**2 + x + 1 # fx = 0.2 + 25.0*x-200*(x**2)+675.0*(x**3)-900.0*(x**4)+400.0*(x**5) a = -1 b = 1 muestras = 51 tolera = 1e-12 iteramax = 100 # PROCEDIMIENTO # Desarrollo analítico con Sympy Fx = sym.integrate(fx,x) Fxn = sym.lambdify('x',Fx,'numpy') Fiab = Fxn(b)-Fxn(a) # Busca igualar trapecio con Integral analitico fxn = sym.lambdify('x',fx,'numpy') base = b-a mitad = base/2 xc = (a+b)/2 # centro diferencia = lambda x: Fiab-base*(fxn(xc-x)+fxn(xc+x))/2 desplazado = op.bisect(diferencia,0,mitad, xtol=tolera,maxiter=iteramax) factor = desplazado/mitad # Integral aproximando con trapecio x0 = xc - factor*mitad x1 = xc + factor*mitad Faprox = base*(fxn(x0)+fxn(x1))/2 # Integral cuadratura Gauss xa = xc + mitad/np.sqrt(3) xb = xc - mitad/np.sqrt(3) FcuadG = base*(fxn(xa)+fxn(xb))/2 erradofactor = np.abs(FcuadG - Faprox) erradoIntegral = np.abs(Fiab-Faprox) # SALIDA print('funcion fx: ', fx) print('Integral Fx: ', Fx) print('I analitico: ', Fiab) print('I aproximado: ', Faprox) print('desplaza centro: ', desplazado) print('factor desplaza: ', factor) print('Factor CuadGauss: ', 1/np.sqrt(3)) print('erradoFactor: ', erradofactor) print('error integral: ', erradoIntegral) # Grafica # Para GRAFICAR # Para gráfica f(x) xi = np.linspace(a,b,muestras) fi = fxn(xi) # Para gráfica Trapecio m = (fxn(x1)-fxn(x0))/(x1-x0) trapeciof = lambda x: fxn(x0)+m*(x-x0) trapecioi = trapeciof(xi) # Areas Trapecio para cada punto que busca k = int(muestras/2) xicg = xi[k:muestras-1] Fcg = [base*(fxn(xi[k+0])+fxn(xi[k-0]))/2] for i in range(1,k,1): untrapecio = base*(fxn(xi[k+i])+fxn(xi[k-i]))/2 Fcg.append(untrapecio) # Punto buscado Fiaprox = base*(fxn(x1)+fxn(x0))/2 Fi = Fxn(xi)-Fxn(a) # Areas de curvas y trapecio plt.subplot(211) # Grafica superior plt.xlim(a,b) plt.plot(xi, fi, label='f(x)') # Solo fi # plt.fill_between(xi,0, fi, # label='integral fi', # color='yellow') # usando cuadratura plt.fill_between(xi,0, trapecioi, label='Cuadratura 2 puntos', color='yellow') plt.axvline(x0,color='white') plt.axvline(x1,color='white') plt.plot([x0,x1],[fxn(x0),fxn(x1)], 'ro', label='x0,x1') plt.axvline(0,color='black') plt.xlabel('x') plt.ylabel('f(x) y Cuadratura de 2 puntos') plt.legend() # Valores de integrales plt.subplot(212) # Grafica inferior plt.xlim(a,b) plt.axhline(Fiab, label='F[a,b]') # plt.plot(xi,Fi,label='F(x)') plt.plot(xicg,Fcg,color='orange',label='Aprox Trapecio') plt.axvline(x1,color='yellow') plt.axvline((1/np.sqrt(3))*(b-a)/2 + xc ,color='magenta') plt.plot(x1,Fiaprox,'ro', label='x0,x1') plt.axvline(0,color='black') plt.xlabel('x') plt.legend() plt.ylabel('Integrando') plt.show()
[ Cuadratura de Gauss ] [ Experimento 2 puntos ] [ Experimento algoritmo ]