2.3 Método de Newton-Raphson – Concepto

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
..

Método de Newton-Raphson

Referencia: Burden 2.3 p49, Chapra 6.2 p148, Rodríguez 3.3 p52

Se deduce a partir de la interpretación gráfica o por medio del uso de la serie de Taylor.

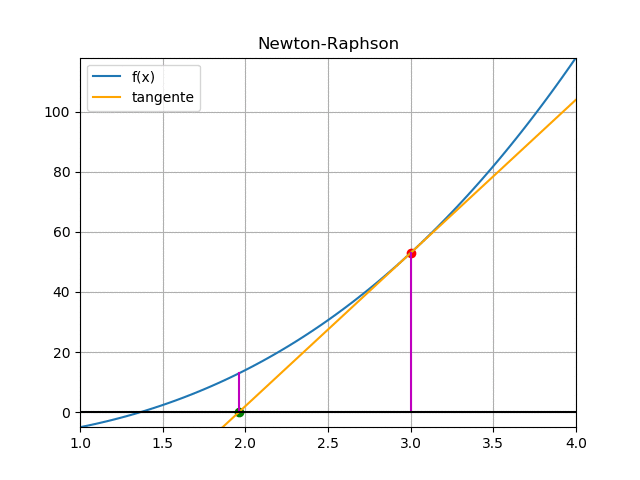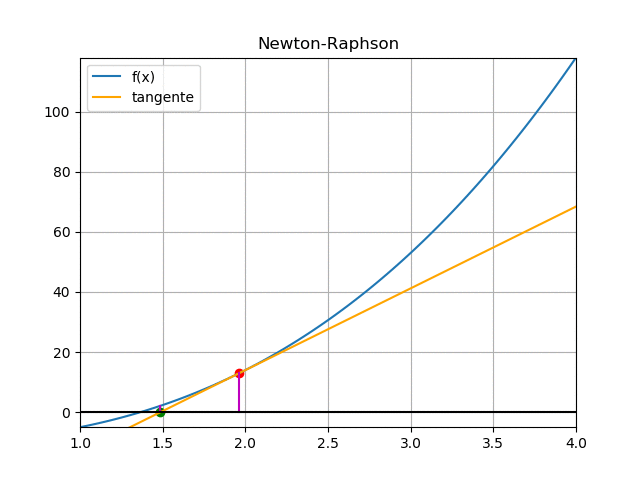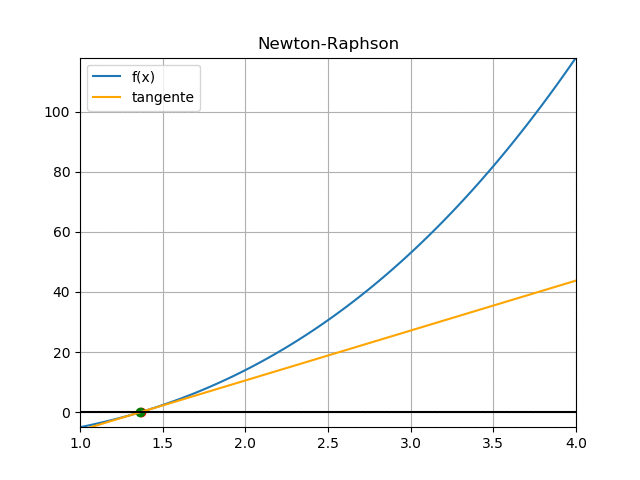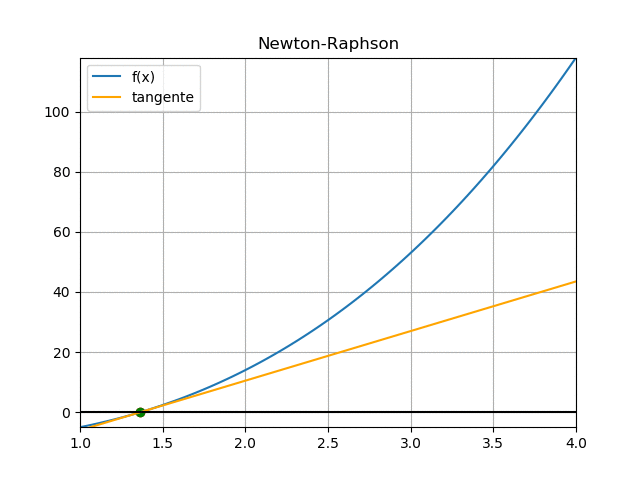
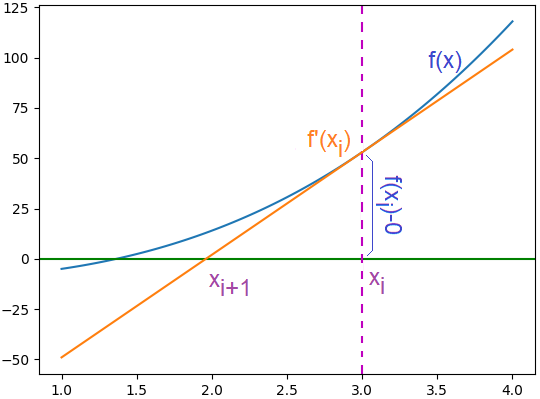
De la gráfica, se usa el triángulo formado por la recta tangente que pasa por f(x_i), con pendiente f'(x_i) y el eje x.

f'(x_i) = \frac{f(x_i) - 0}{x_i - x_{i+1}}

El punto x_i+1 es la intersección de la recta tangente con el eje x, que es más cercano a la raíz de f(x), valor que es usado para la próxima iteración.

Reordenando la ecuación de determina la fórmula para el siguiente punto:

x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}

El error se determina como la diferencia entre los valores sucesivos encontrados |x_i+1 – x_i|

La gráfica animada muestra el proceso aplicado varias veces sobre f(x) para encontrar la raíz.

Tarea

Use la serie de Taylor hasta la primera derivada para encontrar el siguiente punto de aproximación x_i+1

[ Newton-Raphson ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]