s1Eva_IIT2017_T1 Aproximar a polinomio usando puntos

Ejercicio: 1Eva_IIT2017_T1 Aproximar a polinomio usando puntos

Se dispone de tres puntos para la gráfica.

x	f(x)
0	1
0.2	1.6
0.4	2.0

Si el polinomio de Taylor fuera de grado 0, sería una constante, que si se evalúa en x₀ = 0 para eliminar los otros términos, se encuentra que sería igual a 1

Como se pide el polinomio de grado 2, se tiene la forma:

$p(x) = a + bx + c x ^2$ $p(x) = 1 + bx + c x^2$

Se disponen de dos puntos adicionales que se pueden usar para determinar b y c:

$p(0.2) = 1 + 0.2 b + (0.2)^2 c = 1.6$ $p(0.4) = 1 + 0.4 b + (0.4)^2 c = 2.0$

simplificando:

$0.2 b + (0.2)^2 c = 1.6 - 1 = 0.6$ $0.4 b + (0.4)^2 c = 2.0 - 1 = 1$

multiplicando la primera ecuación por 2 y restando la segunda ecuación:

$0 - 0.08 c = 1.2-1 = 0.2$ $c = - 0.2/0.08 = -2.5$

sustituyendo el valor de c obtenido en la primera ecuación

$0.2 b + 0.04(-2.5) = 0.6$ $0.2 b = 0.6 - 0.04(-2.5) = 0.6 + 0.1 = 0.7$ $b = 0.7/0.2 = 3.5$

con lo que el polinomio queda:
$p(x) = 1 + 3.5 x - 2.5 x^2$

validando con python:
tomando los puntos de prueba:

xi = [ 0, 0.2, 0.4]
fi = [ 1, 1.6, 2 ]
>>>

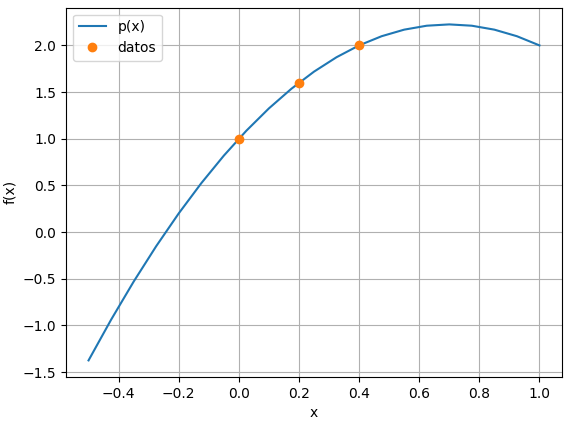
se obtiene la gráfica:

se adjunta las instrucciones usadas para validar que el polinomio pase por los puntos requeridos.

# 1Eva_IIT2017_T1 Aproximar a polinomio usando puntos
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
xi = [ 0, 0.2, 0.4]
fi = [ 1, 1.6, 2 ]

px = lambda x: 1 + 3.5*x - 2.5*(x**2)
a = -0.5
b = 1
muestras = 21

# PROCEDIMIENTO
xj = np.linspace(a,b,muestras)
pxj = px(xj)

# SALIDA
print(xj)
print(pxj)

# Gráfica
plt.plot(xj,pxj,label='p(x)')
plt.plot(xi,fi,'o', label='datos')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.legend()
plt.show()

Nota: Se puede intentar realizar los polinomios aumentando el grado, sin embargo cada término agrega un componente adicional a los términos anteriores por la forma (x – x₀)^k

literal b

se requiere el integral aproximado de f(x) en el intervalo limitado por los 3 puntos de la tabla:

$\int_{0}^{0.4}f(x) dx$

Esta aproximación con un polinomio es el concepto de integración numérica con la regla de Simpson de 1/3, tema desarrollado en la unidad 5

$I_{S13} = \frac{0.2}{3} \Big(1+4(1.6)+ 2 \Big) = 0.62666$