Polinomio de Taylor: [ Ejercicio ] [ función politaylor() ] [ pprint() ]
[ gráfica ] [ función en Sympy ]
..
Ejercicio 1. Taylor para cos(x), tabla y gráfica en Python
Referencia: Burden 7Ed Capítulo 1.1 Ejemplo 3. p11, 10Ed p8. Chapra, 4.1 p80. Taylor Series (Wikipedia)
Continuando con el Ejemplo01, se generaliza el algoritmo para crear una tabla de polinomios de Taylor de diferente grado.
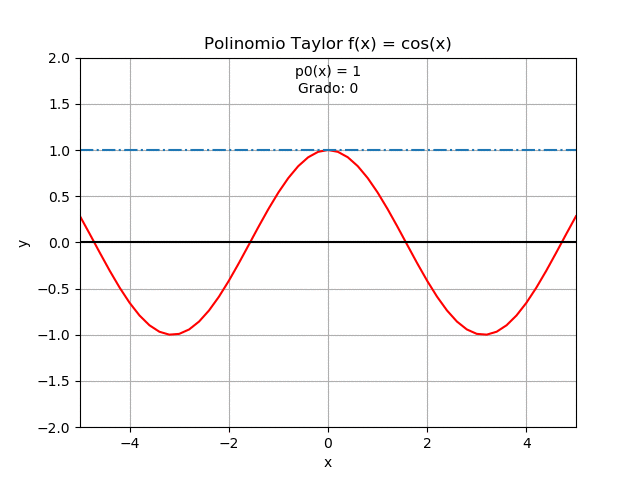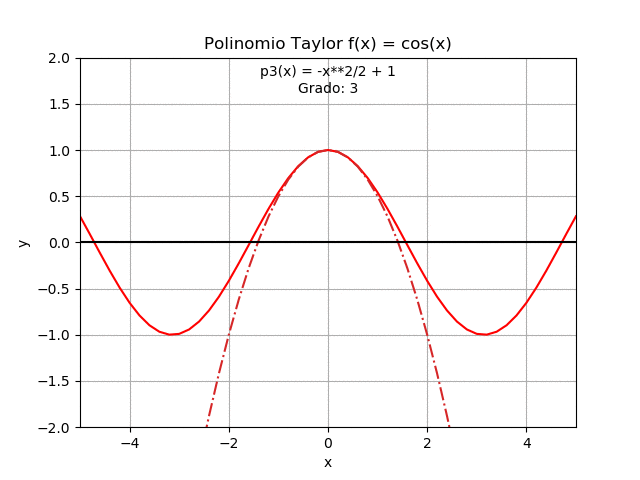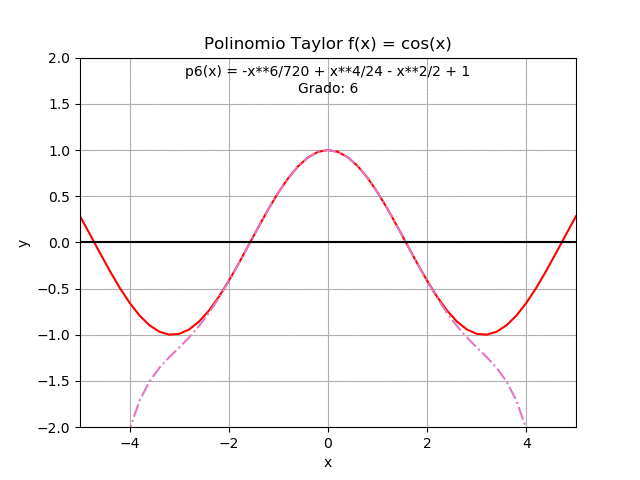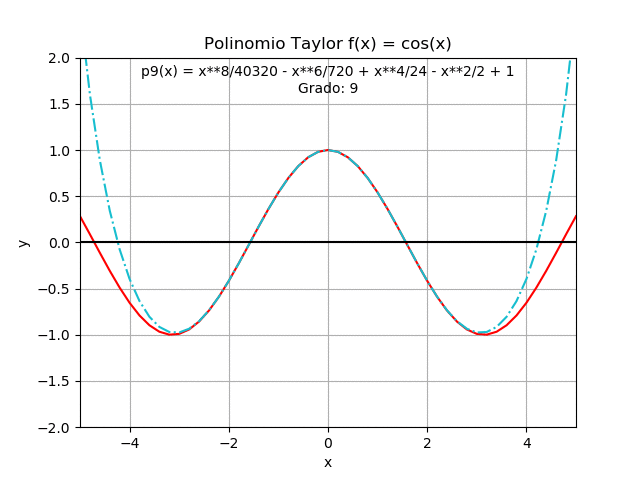
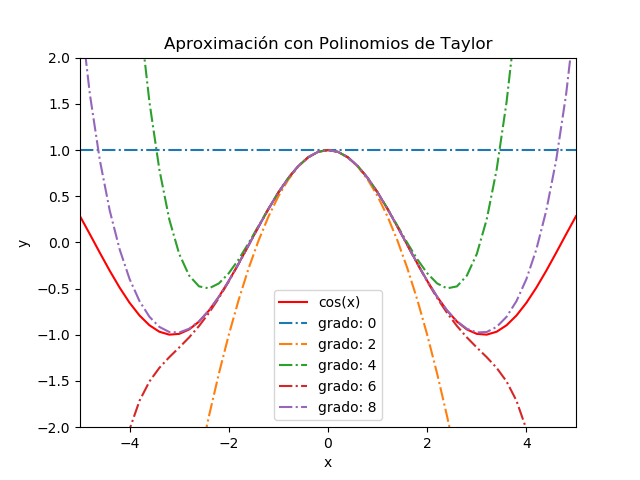
Se complementa el ejercicio con el gráfico de cada polinomio para interpretar los resultados, alrededor de x0 = 0
grado : polinomio 0 : 1 1 : 1 2 : -x**2/2 + 1 3 : -x**2/2 + 1 4 : x**4/24 - x**2/2 + 1 5 : x**4/24 - x**2/2 + 1 6 : -x**6/720 + x**4/24 - x**2/2 + 1 7 : -x**6/720 + x**4/24 - x**2/2 + 1 8 : x**8/40320 - x**6/720 + x**4/24 - x**2/2 + 1 9 : x**8/40320 - x**6/720 + x**4/24 - x**2/2 + 1
Polinomio de Taylor: [ Ejercicio ] [ función politaylor() ] [ pprint() ]
[ gráfica ] [ función en Sympy ]
..
2. Función politaylor(fx,x0,n) en Python
Sección complementaria, no obligatoria para la parte algorítmica
En el ejercicio presentado requiere resolver con varios grados de polinomio, por lo que se generaliza convirtiendo el procedimiento del algoritmo anterior al formato de función def-return. Cada polinomio intermedio se añade a una tabla de resultados:
# Aproximación Polinomio de Taylor alrededor de x0 # f(x) en forma simbólica con sympy import numpy as np import sympy as sym def politaylor(fx,x0,n): k = 0 polinomio = 0 while (k <= n): derivada = fx.diff(x,k) derivadax0 = derivada.subs(x,x0) divisor = np.math.factorial(k) terminok = (derivadax0/divisor)*(x-x0)**k polinomio = polinomio + terminok k = k + 1 return(polinomio) # PROGRAMA ------------- # Capitulo 1 Ejemplo 2, Burden p11, pdf 21 # INGRESO x = sym.Symbol('x') fx = sym.cos(x) x0 = 0 n = 10 # Grado polinomio Taylor a = -5 # intervalo [a,b] b = 5 muestras = 51 # PROCEDIMIENTO # tabla polinomios px_tabla = [] for grado in range(0,n,1): polinomio = politaylor(fx,x0,grado) px_tabla.append(polinomio) # SALIDA print('grado : polinomio') for grado in range(0,n,1): px = px_tabla[grado] print(str(grado)+ ' : '+str(px)) # print('polinomio: ') # sym.pprint(px) # print()
Con lo que se obtiene los polinomios para cada grado calculado.
grado : polinomio 0 : 1 1 : 1 2 : -x**2/2 + 1 3 : -x**2/2 + 1 4 : x**4/24 - x**2/2 + 1 5 : x**4/24 - x**2/2 + 1 6 : -x**6/720 + x**4/24 - x**2/2 + 1 7 : -x**6/720 + x**4/24 - x**2/2 + 1 8 : x**8/40320 - x**6/720 + x**4/24 - x**2/2 + 1 9 : x**8/40320 - x**6/720 + x**4/24 - x**2/2 + 1
Polinomio de Taylor: [ Ejercicio ] [ función politaylor() ] [ pprint() ]
[ gráfica ] [ función en Sympy ]
..
3. Otras formas de presentación del polinomio
Otra forma de presentar la salida es ¨pretty print¨ con sym.pprint(), borre los # de las tres últimas líneas de código para obtener:
grado : polinomio
0 : 1
polinomio:
1
1 : 1
polinomio:
1
2 : -x**2/2 + 1
polinomio:
2
x
- -- + 1
2
3 : -x**2/2 + 1
polinomio:
2
x
- -- + 1
2
4 : x**4/24 - x**2/2 + 1
polinomio:
4 2
x x
-- - -- + 1
24 2
5 : x**4/24 - x**2/2 + 1
polinomio:
4 2
x x
-- - -- + 1
24 2
6 : -x**6/720 + x**4/24 - x**2/2 + 1
polinomio:
6 4 2
x x x
- --- + -- - -- + 1
720 24 2
Polinomio de Taylor: [ Ejercicio ] [ función politaylor() ] [ pprint() ]
[ gráfica ] [ función en Sympy ]
..
4. Gráfica de resultados
La forma gráfica de cada polinomio se obtiene evaluando cada polinomio para obtener las líneas en el intervalo [a, b] para cada punto del vector xi .
Se utiliza un cierto número de muestras en cada intervalo [a,b].
El resultado es una matriz, px_lineas, cuya fila representa el grado del polinomio, y la columna contiene los valores del polinomio de cada grado evaluado en cada punto xi
# GRAFICA - TABLA polinomios ------ xi = np.linspace(a,b,muestras) # Forma lambda, simplifica evaluación fxn = sym.utilities.lambdify(x,fx,'numpy') fi = fxn(xi) # lineas de cada grado de polinomio px_lineas = np.zeros(shape=(n,muestras), dtype =float) for grado in range(0,n,1): polinomio = px_tabla[grado] px = sym.utilities.lambdify(x,polinomio,'numpy') px_lineas[grado] = px(xi)
los valores se pueden graficar añadiendo las siguientes instrucciones:
# SALIDA - GRAFICA import matplotlib.pyplot as plt plt.plot(xi,fi,'r',label=str(fx)) for grado in range(0,n,2): etiqueta = 'grado: '+str(grado) plt.plot(xi, px_lineas[grado], '-.',label = etiqueta) ymax = 2*np.max(fi) plt.xlim([a,b]) plt.ylim([-ymax,ymax]) plt.xlabel('x') plt.ylabel('y') plt.title('Aproximación con Polinomios de Taylor') plt.legend() plt.show()
Polinomio de Taylor: [ Ejercicio ] [ función politaylor() ] [ pprint() ]
[ gráfica ] [ función en Sympy ]
..
5. Función de Sympy para polinomio de Taylor
Existe la función desarrollada en Sympy para generar el polinomio. Se muestra un ejemplo del uso de la función como referencia.
>>> import sympy as sym
>>> x = sym.Symbol('x')
>>> fx = sym.cos(x)
>>> polinomio = sym.series(fx,x,x0=0, n=3)
>>> polinomio
1 - x**2/2 + O(x**3)
>>>
Polinomio de Taylor: [ Ejercicio ] [ función politaylor() ] [ pprint() ]
[ gráfica ] [ función en Sympy ]