ESTG1003 – FCNM – ESPOL
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 4 (15 puntos). La entrada a un filtro es un ruido blanco con media cero y densidad espectral de potencia N0/2.
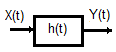El filtro tiene la función de transferencia mostrada:
a) Encuentre SY,X(f) y RY,X(τ)
b) Encuentre SY(f) y RY(τ)
c) Calcule la potencia promedio del proceso de salida
Rúbrica: literal a (6 puntos), literal b (6 puntos), literal c (3 puntos)
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 3. (15 puntos) Encuentre la densidad espectral de potencia SY(f) de un proceso aleatorio con función de auto-correlación:
RX(τ) cos(2 π f0 τ)
donde RX(τ) es en si mismo una función de auto-correlación.
Determine la potencia promedio, si RX(τ) es de tipo triangular y grafique Sy(f).
Rúbrica: Sy(f) (5 puntos), potencia promedio (5 puntos) Sy(f) nueva(5 puntos)
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 2. (45 puntos) Sean X(t) y Y(t) mostrados en la figura, donde θ es una variable aleatoria uniforme, distribuida en el rango [-π π].
X(t) = \cos (\omega t + \theta) Y(t) = \sin (\omega t + \theta)Como ejemplo, si ω = 1/2, para θ = 0 y θ = π/4, se muestran los resultados en la figura sobre X(t) y Y(t).
Determine los resultados para:
a) Valor esperado de X(t)
b) Valor esperado de Y(t)
c) Correlación cruzada entre X(t) y Y(t)
d) Covarianza cruzada de X(t) y Y(t)
e) Determinar si el proceso Y es estacionario o estacionario en el sentido amplio. Justifique su respuesta
Rúbrica: literal a y b (5 puntos cada uno), literal c (20 puntos), literal d (5 puntos), literal e) (10 puntos)
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 1 (25 puntos). Sea Y una variable aleatoria definida por:
donde X es una variable aleatoria uniforme, distribuida en el intervalo
de (0, T ]
a) Determine la función densidad de probabilidad para Y
b) Calcule la función de distribución acumulada para Y
c) Grafique su resultado
d) Determine la auto-correlación para Y
Rúbrica: literal a (10 puntos), literal b, c, d (5 puntos cada uno)
Tema 5 (10 puntos). Si el proceso estocástico X(t) del tema anterior pasa por un sistema con función de transferencia h(t)
h(t) = 4 e^{-2t} \mu (t)
a) Determine la densidad espectral de potencia en la salida
b) Calcule la potencia promedio del proceso en la salida
Tema 4 (20 puntos) Asuma un proceso estocástico X(t) estacionario en el sentido amplio con función de auto-correlación
R_x(t) = e^{-|\tau |}, \tau \in \Re
a) Determine la densidad espectral de potencia del proceso A(t) = X(t) − X(t−1)
b) Calcule la potencia promedio del proceso A(t)
Tema 3 (20 puntos). Considere el proceso estocástico estacionario en el sentido amplio X(t) con media cero y con auto-correlación
R_x = 50 \cos (20 \pi \tau) + 18 \cos (30 \pi \tau)
a) Determine Var(X(t))
b) Determine la potencia promedio
c) Calcule la densidad espectral de potencia SX(f)
Tema 2 (25 puntos). Dado el proceso o señal descrito por: 
X(t) = cos(ω t + Φ)
donde Φ es una variable aleatoria uniforme en el intervalo (-π, π)
a) Encuentre la auto-covarianza de X(t).
b) Determinar y si el proceso es estacionario o estacionario en el sentido amplio. Justifique su respuesta
c) Determine si la densidad espectral de potencia SX(f)
Tema 1. (25 puntos). Dado el proceso o señal descrito por: 
Y=cos(X)
Suponga que X es una variable aleatoria uniforme, distribuida en el intervalo de (0, 2π].
a) Determine la función densidad de probabilidad para Y
b) Calcule la función de distribución acumulada para Y
c) Grafique su resultado