Publicado en

2.1 Valor Esperado E[x] a partir de pmf – Ejercicio

Referencia: LoRaWan – Descriptor estadístico de un punto en Girni,

El indicador de fuerza de la señal recibida (RSSI) para un dispositivo a una distancia desde el gateway es un valor entero que se encuentra alrededor el valor esperado o media. Las condiciones del ambiente generan un componente aleatorio que se muestra en la figura.

Las mediciones se pueden obtener para el enlace de subida (dispositivo a gateway) o enlace de bajada (gateway a dispositivo). A partir de los valores se pueden obtener la pmf del enlace de subida o de bajada

Ejercicio

A partir de los datos de los datos obtenidos para un punto con ubicación  etiquetada LOS04, calcular el valor esperado para los enlaces de subida (UP) y de bajada (Down) a partir de los siguientes datos, presentados en forma de un diccionario de Python:

{"pmf":
 {"pmf_down":
  {"intervalo":[-70,-69,-68,-67,-66,-65,-64],
   "freq_relativa":[0.036101083,0.1371841155,0.1732851986,0.1624548736,0.2707581227,0.202166065,0.0180505415]
   },
  "pmf_up":
  {"intervalo":[-83,-82,-81,-80,-79,-78,-77,-76,-75,-74,-73,-72,-71,-70,-69,-68,-67,-66,-65,-64,-63,-62,-61,-60,-59,-58,-57],
   "freq_relativa":[0.036101083,0.0,0.0252707581,0.0,0.0072202166,0.0,0.1010830325,0.0036101083,0.1083032491,0.0,0.1227436823,0.0,0.0433212996,0.0324909747,0.0180505415,0.0252707581,0.0685920578,0.1335740072,0.0288808664,0.0,0.1046931408,0.1046931408,0.0180505415,0.0072202166,0.0072202166,0.0,0.0036101083]
   }
  },
 "dispositivo":{"pmf_down":"cc24","pmf_up":"cc24"}
 }
Publicado en

PAM a PSK – valor esperado

Y(t)=acos⁡(2πt+π2X(t)) Y(t) = a \cos \big( 2\pi t + \frac{\pi}{2}X(t) \big)

La pmf de x(t) es 0.5 para cada valor de [-1,1]

c) Encuentre la media y autocorrelación de Y(t)

E[Y(t)]=E[acos⁡(2πt+π2X)] E[Y(t)] = E\big[ a \cos \big( 2\pi t + \frac{\pi}{2}X \big)\big]

Referencia:  León-García 3.3.1 p. 107. Valor esperado de funciones de variable aleatoria

Si z =g(x)

E[g(x)]=∑kg(xk)px(Xk) E[g(x)] = \sum_k g(x_k)p_x(X_k)

se tiene entonces que:

=[acos⁡(2πt+π2(−1))]12+[acos⁡(2πt+π2(1))]12 = \big[a \cos \big( 2\pi t + \frac{\pi}{2}(-1) \big)\big]\frac{1}{2} + \big[a \cos \big( 2\pi t + \frac{\pi}{2}(1) \big)\big] \frac{1}{2} =a2cos⁡(2πt−π2)+a2cos⁡(2πt+π2) = \frac{a}{2}\cos \big( 2\pi t - \frac{\pi}{2} \big) + \frac{a}{2}\cos \big( 2\pi t + \frac{\pi}{2} \big) =a2sin⁡(2πt)−a2sin⁡(2πt)=0 = \frac{a}{2} \sin \big( 2\pi t \big) - \frac{a}{2} \sin \big( 2\pi t \big) = 0 E[Y(t)]=0 E[Y(t)] = 0
Publicado en

1. Valor Esperado de una función de variable aleatoria

Referencia: Gubner 2.4 p83 , Ross 2.4.3 p42, León-García 3.3.1 p.107

Dada una variable aleatoria X, se puede definir una nueva variable aleatoria Z = g(X), donde g(x) es una función de valor real de la variable real x.

Para calcular E[Z] se puede proceder como:

E[g(X)]=∑ig(xi)pX(xi) E[g(X)] = \sum_i g(x_i) p_X(x_i) E[g(x)]=∫−∞∞g(x)f(x)dx E[g(x)] = \int_{-\infty}^{\infty} g(x) f(x) dx

dado que la fórmula es mas fácil de usar que encontrar la pmf de Z, la formula se la conoce como la «ley del estadístico inconsciente» o LOTUS (Law Of The Unconscious Statistician).

Una aplicación simple es :

E[aX]=∑iaxipX(xi)= E[aX] = \sum_i ax_i p_X(x_i) = =a∑ixipX(xi)=aE[X] = a \sum_i x_i p_X(x_i) = a E[X]

Ejemplo

Referencia: León- García 3.17 p107

Sea X el ruido en el voltaje que está uniformemente distribuido en SX = {-3,-1,+1,+3} con pX (k) =  1/4 para k en SX. Encuentre E[Z] donde Z=X2.

Solución: Se busca primero encontrar la pmf (probability mass function) de Z, el SZ ={9,1,1,9} = {1,9}, por lo que:

pZ(9) = P[X ∈ {-3,+3}] 
      = pX(-3) + pX(3) 
      = 1/4 + 1/4 = 1/2
pZ(1) = pX(-1) + pX(1) = 
      = 1/4 + 1/4 = 1/2
entonces:
E[Z] = 1(1/2) + 9(1/2) = 5

usando la fórmula para E[Z]:

E[Z]=E[g(X)]=∑ig(xi)pX(xi)= E[Z] = E[g(X)] = \sum_i g(x_i)p_X(x_i) = ∑ii2pX(xi)=14[(−3)2+(−1)2+12+22]= \sum_i i^2 p_X(x_i) = \frac{1}{4} [(-3)^2 + (-1)^2+1^2+2^2] = =204=5 = \frac{20}{4} = 5

con lo que se obtuvo el mismo resultado.

Ross Corolario 2.2. Siendo a y b constantes, entonces:

E[aX+b]=aE[X]+b E[aX + b] = aE[X] +b
Publicado en

3. Valor Esperado de variables aleatorias contínuas

Referencia: Ross 2.4.2 p39, Gubner 4.2 p149, León-García 4.3 p 155, p16

Si X es una variablea aleatoria contínua que tiene una función densidad de probabilidad f(x), el valor esperado de X se define como:

E[X]=∫−∞∞xf(x)δx E[X]= \int_{-\infty}^{\infty}xf(x) \delta x

Ejemplo

Referencia: Ross 4.7.

Sea X una variable aleatoria contínua uniforme [a,b], encuentre el valor esperado:

Solución:

E[X]=∫−∞∞xf(x)δx=∫abx1b−aδx= E[X]= \int_{-\infty}^{\infty} xf(x) \delta x = \int_{a}^{b} x\frac{1}{b-a}\delta x = =1(b−a)x22∣ab=1(b−a)b2−a22= \left. = \frac{1}{(b-a)} \frac{x^2}{2} \right|_{a}^{b} = \frac{1}{(b-a)} \frac{b^2-a^2}{2} = =(b+a)(b−a)2(b−a)=a+b2 = \frac{(b+a)(b-a)}{2(b-a)} = \frac{a+b}{2}

que es el promedio simple entre a y b cuando la función es uniforme.

Ejemplo

Ross 4.8/Leon-García 4.20. Un convertidor analógico-digital o cuantizador con resolución de paso Δ voltios redondea en la entrada el valor más cercano al múltiplo de Δ voltios como se muestra en la figura.

La entrada es un voltaje Vin de tipo aleatorio y la salida del convertidor es A/D es Vout, y su desempeño se mide por el error cuadratico medio:

E[|Vin – Vout|2]

Se supone que el error Vin – Vout se puede aproximar a una función aleatoria uniforme [-Δ/2,Δ/2] dado que siempre el valor siempre cae en el intervalo dado. Determine el valor esperado para la señal de entrada, y también el valor del error cuadrático medio.

Solución: Para el intervalo centrado en el origen

f(x)=1b−a f(x)= \frac{1}{b-a} E[X]=∫−Δ/2Δ/2xf(x)δx= E[X] = \int_{-\Delta /2}^{\Delta /2} xf(x) \delta x = =∫−Δ/2Δ/2x1Δ/2−(−Δ/2)δx =\int_{-\Delta /2}^{\Delta /2} x\frac{1}{\Delta /2 - (-\Delta /2)} \delta x =∫−Δ/2Δ/2xΔδx=x22Δ∣−Δ/2Δ/2 = \int_{-\Delta /2}^{\Delta /2} \frac{x}{\Delta} \delta x = \left. \frac{x^2}{2 \Delta} \right|_{-\Delta /2}^{\Delta /2} =12Δ[(−Δ2)2−(Δ2)2]=0 = \frac{1}{2\Delta} \big[ {\big( \frac{-\Delta}{2}\big)}^2 - {\big( \frac{\Delta}{2}\big)}^2 \big] = 0

Para el error cuadrático medio en [a,b], a=-Δ/2, b=Δ/2

E[∣Vin−Vout∣2]≈E[X2] E[|V_{in}-V_{out}|^2] \approx E[X^2] =∫−∞∞x2f(x)δx=∫abx21b−aδx = \int_{-\infty}^{\infty} x^2 f(x) \delta x = \int_{a}^{b} x^2 \frac{1}{b - a} \delta x =1b−ax33∣ab=1b−ab3−a33= = \left. \frac{1}{b-a} \frac{x^3}{3} \right|_{a}^{b} = \frac{1}{b-a} \frac{b^3-a^3}{3} = =(b−a)(b2+ba+a2)3(b−a) = \frac{(b-a)(b^2+ba+a^2)}{3(b-a)} =b2+ba+a23 = \frac{b^2+ba+a^2}{3} =(Δ2)2+(Δ2)(−Δ2)+(−Δ2)23 = \frac{({\frac{\Delta}{2})}^2 + {(\frac{\Delta}{2})}{(\frac{-\Delta}{2})} + {(\frac{-\Delta}{2})}^2}{3} =13Δ2−Δ2+Δ24=Δ212 = \frac{1}{3} \frac{\Delta ^2 -\Delta^2 + \Delta ^2}{4} = \frac{\Delta ^2}{12}
Publicado en

2. Valor Esperado E[x] a partir de pmf

Referencia: León-García p.104, Gubner p.80,

Para describir el comportamiento de una variable aleatoria discreta a partir de su  funciones de distribución de probabilidad (pmf, probability mass function), para simplificar en un solo valor, se usa el valor esperado o media.

El valor esperado o media de una variable aleatoria discreta X se define como:

mx=E[X]=∑x∈Sxxpx(x)= m_x = E[X] = \sum\limits_{x \in S_x} x p_x(x) = =∑kxkpx(xk) = \sum\limits_{k} x_k p_x(x_k)

El valor esperado E[X] está definido si la suma anterior absolutamente converge , es decir:

E[∣X∣]=∑k∣xk∣px(xk)<∞ E[|X|] = \sum\limits_{k} |x_k| p_x(x_k) < \infty

Ejemplo

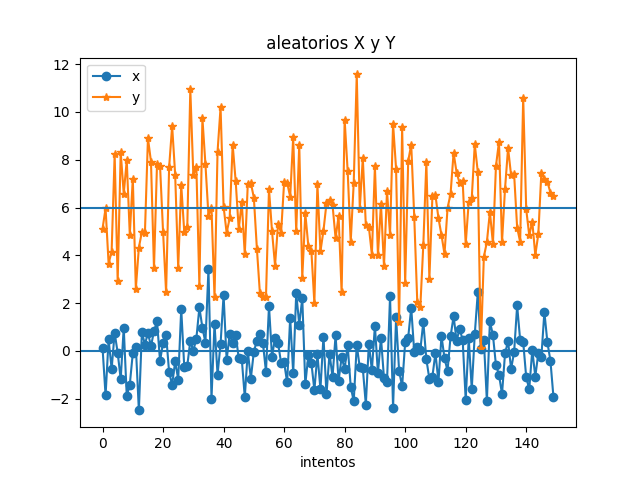
De repetir un experimento 150 veces, se obtienen dos variables aleatorias.

  • La variable Y tiene valores alrededor de 0,
  • mientras que la variable X tiene valores alrededor de 6 .
  • También observe que X tiene mayor variación que Y.

Siendo px(x) la función de distribución de probabilidad de los puntos x1, x2, … , entonces E[x] representa el centro de masa de la distribución.

Ejemplo: Media de una variable aleatoria tipo Bernoulli

(Ejemplo 3.11) Encuentre el valor de la variable aleatoria IA:

E[IA]=0pi(0)+1p1(1)=p E[I_A] = 0p_i(0) + 1p_1(1) = p

donde p es la probabilidad de éxito de una prueba Bernoulli.

Ejemplo: Tres lanzamientos de una moneda y la variable aleatoria Binomial

(Ejemplo 3.12)Sea X el número de caras en tres lanzamientos de una moneda, Encuentre E[X]

E[X]=∑k=03kpx(k) E[X] = \sum \limits_{k=0}^{3} k p_x(k)

las probabilidades de que salgan 0 caras es 1/8, 1 cara es 3/8, 2 caras 3/8 y 3 caras 1/8, resultados obtenidos en el ejemplo 3.5 del libro

=0(18)+1(38)+2(38)+3(18) = 0 \big( \frac{1}{8} \big) + 1 \big(\frac{3}{8} \big) + 2\big(\frac{3}{8} \big) + 3\big(\frac{1}{8} \big) =128=1.5 = \frac{12}{8} =1.5

Ejemplo: Media de una variable aleatoria uniforme

Se conoce que px(j) = 1/M, para j=0, … , M-1, entonces:

E[X]=∑k=0M−1k1M E[X] = \sum \limits_{k=0}^{M-1} k \frac{1}{M} =1M[0+1+2+...+M−1] =\frac{1}{M}[ { 0 + 1 + 2 + ... + M-1}] =(M−1)M2M=M−12 = \frac{(M-1)M}{2M} = \frac{M-1}{2}

El término de «valor esperado» no quiere decir que esperamos observar E[X] cuando se ejecuta un experimento que genera X.

Por ejemplo, el valor esperado de un intento Bernoulli es p, pero sus resultados siempre son 0 ó 1.

E[X] corresponde al «promedio de X» en un gran número de observaciones de X.

El promedio aritmético o media muestral de las observaciones cuando el número de muestras n tiende a ser grande converge al valor esperado:

⟨X⟩n=∑kxkfk(n)→ \langle X\rangle_n = \sum\limits_{k} x_k f_k(n) \rightarrow →∑kxkpx(xk)=E[x] \rightarrow \sum\limits_{k} x_k p_x (x_k) = E[x]

Instrucciones en Python

Para generar valores aleatorios con media y escala conocida se puede usar la función stats.norm.rvs(media, escala, muestras, obteniendo algunos valores como:

px: 
[-1  0 -1 -2  3  0 -1  0  0  0  1  0  0  0  0  0  1  1 -1  0  0 -1  0  0
  0  0  1  0  0  0  0  1  0  0  0  0  0  0  0  0  0  0  0  0  1  0  0  0
...]
py: 
[ 8  4  6  6  2  5  2  3  6  6  7  6  4  5  2  6  4  4  6  7  7  4  4  5
  5  4  4  3  2  9  5  8  5  6  7  2  4  1  1  6  5  7  6  7  4  7  9  5
...]
# Valor Esperado E[x] a partir de pmf
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats

# INGRESO
n = 150

media_x = 0
escala_x = 1

media_y = 6
escala_y = 2

# PROCEDIMIENTO
px = stats.norm.rvs(media_x,escala_x,size=n)
px = np.array(px,dtype=int)
py = stats.norm.rvs(media_y,escala_y,size=n)
py = np.array(py,dtype=int)

# SALIDA
print('px: ')
print(px)
print('py: ')
print(py)
# grafica
plt.title(' aleatorios X y Y')
plt.plot(px, 'o-', label='x')
plt.plot(py, '*-', label='y')
plt.xlabel('intentos')
plt.axhline(media_x)
plt.axhline(media_y)
plt.legend()
plt.show()