Ejemplo: León-García 4.20 p.161
Un cuantizador se usa para convertir una señal analógica (ejemplo: audio) en su forma digital.
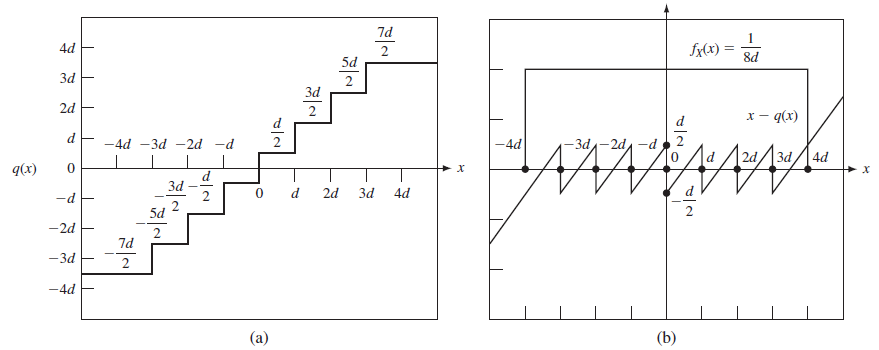
Un cuantizador crea un mapa de un voltaje aleatorio X en el punto más próximo q(X) a los valores 2R representados como se muestra en la figura.
El valor de X se aproxima por q(X), el que se identifica con un número binario de R-bits. De esta forma, un voltage «analógico» X , que toma valores contínuos se convierte a un numero de R-bits.
El cuantizador introduce un error Z = X – q(X) como se muestra en la figura (b). Note que Z es una función de X y cuyo rango está entre -d/2 y d/2, conocido como el tamaño de paso del cuantizador.
Suponga que X tiene una distribución uniforme en el intervalo [-xmax, xmax], que el cuentizador tiene 2R niveles, y que 2xmax = 2Rd.
Es sencillo mostrar que > está uniformemente distribuido en el intervalo [-d/2, d/2].
Se tiene que para una variable uniforme:
E[X]= \frac{1}{b-a}\int_{a}^{b}t dr = \frac{a+b}{2}
E[z] = \frac{d/2 - d/2}{2} = 0
El error Z tiene media cero.
La varianza es:
VAR[Z] =\frac{(d/2 - (-d/2)^2}{12} =\frac{d^2}{12}
El resultado es aproximadamente correcto para cualquier pdf que sea aproximadamente plana sobre un intervalo del cuantizador. Es el caso cuando 2R es grande.
La aproximación de q(x) puede ser observada como una versión «ruidosa» de X, dado que:
Q(Z) = X-Z
donde Z es el error de cuantización, Una medida de cuán bueno es el cuantizador se da por el factor SNR o de señal ruido, que se define como la fracción entre la varianza de la «señal» X para la varianza de la distorción de «ruido» Z:
\text{SNR} = \frac{VAR[X]}{VAR[Z]} = \frac{VAR[X]}{d^2 /12}
= \frac{VAR[X]}{x_{max}^2 /3} 2^{2R}
donde se ha usado el hecho que d= 2xmax/ 2R.
Cuando X es no uniforme, el valor de xmax se seleccciona de tal forma que P[|X|> xmax] sea pequeña. Un casi tipico es que xmax = 4 STD[X], con lo que SNR será:
\text{SNR} = \frac{3}{16} 2^{2R}
lo que es genera la formula conocida como:
\text{SNR dB} = 10 log_{10} \text{SNR} = 6R-7.3 dB
En otras palabras, el nivel de SNR se incrementa por un factor de 4 (6db) con cada bit adicional que se usa para representar X. Esto tiene sentido dado que cada bit duplica el número de niveles de cuantización, lo cual reduce el tamaño de paso por un factor de 2. La varianza del error podría ser reducida por el cuadrado de ésto, es decir 22=4