Funciones de una Variable aleatoria – Procesos Estocásticos

Sea X una variable aleatoria y sea g(x) una función de valor real definida en el eje real.

Defina Y= g(X), esto es. Y está determinada por la evaluación de la función en g(x) en el valor que ha tomado la variable aleatoria X. Entonces Y también es una variable aleatoria.

Las probabilidades de los valores para Y dependen de la función g(x) así como la función distribución acumulada de X.

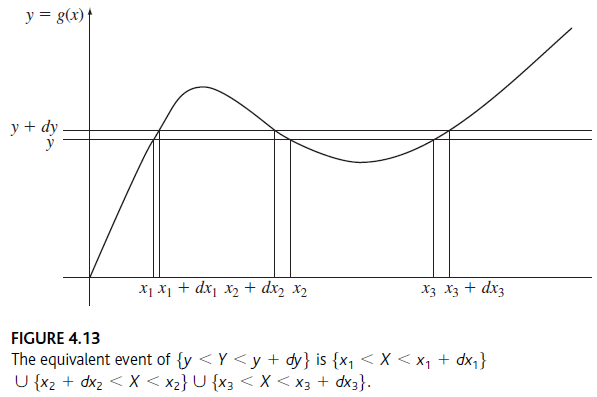
Considere una función no lineal Y=g(X) como la que se muestra en la figura.

donde |dy| es la longitud del intervalo y < Y ≤ (y+dy).
De forma similar, la probabilidad que el evento en cada intervalo es aproximadamente

f_Y(y)=\left.\sum_{k} \frac{f_X(x)}{|dy/dx|} \right|_{x=x_k}

=\left.\sum_{k} f_X(x) \left| \frac{dx}{dy} \right| \right|_{x=x_k}

Ejemplo: León García 4.30 p.176

Sea X el valor de las muestras de voltaje de una señal de voz, y suponga que X tiene una distribución uniforme en el intervalo [-4d,4d].

Sea Y = q(X), donde la función característica de entrada-salida de un cuantizador (convertidor analógico-digital) se muetra en la figura. Encuentre la función de probabilidad de masa para Y.

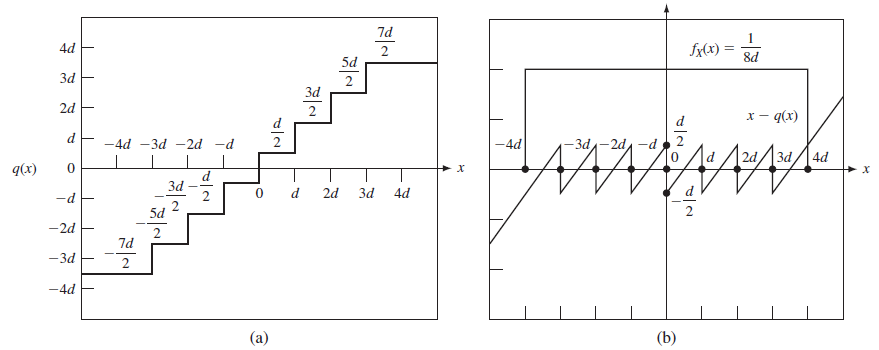
Solución: El evento {Y=q} para q en S_Y es equivalente al evento {X en I_q}, donde Iq es un intervalo de puntos equivalentes mapeados en representación al punto q. La pmf de Y se encuentra evaluando:
$P[Y=q] = \int_{I_q} f_X(t) dt$

Lo que permite ver fácilmente que la representación de un punto tiene un intervalo de longitud d mappeado en él. Entonces existirán ocho posibles salidas equiprobables, es decir, P[Y=q] = 1/8 para q en S_Y–