[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
1. Integrales Dobles sobre área rectangular
Referencia: Chapra 21.5 p643, Burden 4.9 p174
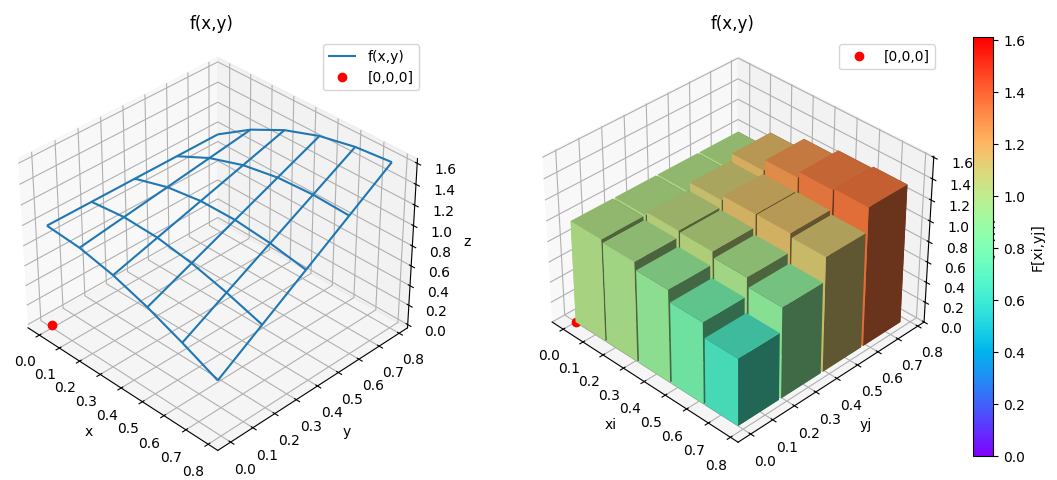
Un ejemplo sencillo de integral doble es una función sobre un área rectangular. Las técnicas revisadas en las secciones anteriores de pueden reutilizar para la aproximación de integrales múltiples. 
Considere la integral doble
\int_R \int f(x,y) \delta Asiendo
R = {(x,y) |
x0 ≤ x ≤ xn,
y0 ≤ y ≤ yn }
que es una región rectangular en el plano.
\int_{x_o}^{x_n}\int_{y_o}^{y_n} f(x,y) \delta y \delta x \int_{y_o}^{y_n} \int_{x_o}^{x_n} f(x,y) \delta x \delta y[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
2. Ejercicio
Referencia: 3Eva_IIT2018_T1 Integral doble con Cuadratura de Gauss
Aproxime el resultado de la integral doble (en área rectangular)
\displaystyle \int_{0}^{\pi/4} \displaystyle\int_{0}^{\pi/4} \Big( 2y \sin(x) + \cos ^2 (x) \Big) \delta y \delta xConsidere los tramosx = 5 como tamaños de paso en eje x , tramosy = 4 como tamaños de paso en eje y.
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
3. Desarrollo Analítico
Use las fórmulas compuestas de Simpson, haciendo primero constante un valor en y, luego propagando el proceso. Al obtener los integrales en un sentido, repetir el proceso con los resultados en el otro eje.
j: 0 , yj[0]: 0.0 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.4378989163640264 Simpson 1/3 : 0.20482799857900125 j: 1 , yj[1]: 0.19634954084936207 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.4807008818748735 Simpson 1/3 : 0.2770455037573468 j: 2 , yj[2]: 0.39269908169872414 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.5235028473857204 Simpson 1/3 : 0.34926300893569256 j: 3 , yj[3]: 0.5890486225480862 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.5663048128965673 Simpson 1/3 : 0.42148051411403814 j: 4 , yj[4]: 0.7853981633974483 Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] Simpson 3/8 : 0.6091067784074142 Simpson 1/3 : 0.4936980192923838 Fórmulas compuestas, tramos: 4 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 1 0] Simpson 3/8 : 0.4802254950852897 trapecio : 0.20524320554554915 xi [0. 0.1571 0.3142 0.4712 0.6283 0.7854] yj [0. 0.1963 0.3927 0.589 0.7854] f(x,y) [[1. 0.9755 0.9045 0.7939 0.6545 0.5 ] [1. 1.037 1.0259 0.9722 0.8853 0.7777] [1. 1.0984 1.1472 1.1505 1.1162 1.0554] [1. 1.1598 1.2686 1.3287 1.347 1.333 ] [1. 1.2213 1.3899 1.507 1.5778 1.6107]] Integral Volumen: 0.6854687006308389
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
4. Algoritmo en Python
El punto de partida es usar las Fórmulas compuestas con Δx segmentos desiguales, donde el algoritmo selecciona aplicar Simpson 3/8, Simpson 1/3 y trapecios según se cumplan los requisitos.
Instrucciones en Python
# 3Eva_IIT2018_T1 Integral doble con Cuadratura de Gauss # Integrales de volumen o dobles import numpy as np # INGRESO fxy = lambda x,y: 2*y*np.sin(x)+(np.cos(x))**2 x0 = 0 # intervalo x xn = np.pi/4 y0 = 0 # intervalo y yn = np.pi/4 tramosx = 5 # tramos por eje tramosy = 4 titulo = 'f(x,y)' precision = 4 # decimales a mostrar # PROCEDIMIENTO xi = np.linspace(x0,xn,tramosx+1) yj = np.linspace(y0,yn,tramosy+1) n = len(xi) m = len(yj) hx = (xn-x0)/tramosx # tamaños de paso hy = (yn-y0)/tramosy Xi,Yj = np.meshgrid(xi,yj) # Matriz u[xi,yj] para f(x,y) F = np.zeros(shape=(n,m),dtype=float) F = fxy(Xi,Yj) def simpson_compuesto(xi,fi,vertabla=False,casicero=1e-7): '''Método compuesto Simpson 3/8, Simpson 1/3 y trapecio salida: integral,cuenta_h ''' # vectores como arreglo, numeros reales xi = np.array(xi,dtype=float) fi = np.array(fi,dtype=float) n = len(xi) # Método compuesto Simpson 3/8, Simpson 1/3 y trapecio cuenta_h = (-1)*np.ones(n,dtype=int) # sin usar suma = 0 # integral total suma_parcial =[] # integral por cada método i = 0 while i<(n-1): # i<tramos, al menos un tramo tramo_usado = False h = xi[i+1]-xi[i] # tamaño de paso, supone constante # tres tramos iguales if (tramo_usado==False) and (i+3)<n: d2x = np.diff(xi[i:i+4],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 3/8 S38 = (3/8)*h*(fi[i]+3*fi[i+1]+3*fi[i+2]+fi[i+3]) suma = suma + S38 cuenta_h[i:i+3] = [3,0,0] # Simpson 3/8 suma_parcial.append(['Simpson 3/8',S38]) i = i+3 tramo_usado = True # dos tramos iguales if (tramo_usado==False) and (i+2)<n: d2x = np.diff(xi[i:i+3],2) # diferencias entre tramos errado = np.max(np.abs(d2x)) if errado<casicero: # Simpson 1/3 S13 = (h/3)*(fi[i]+4*fi[i+1]+fi[i+2]) suma = suma + S13 cuenta_h[i:i+2] = [2,0] suma_parcial.append(['Simpson 1/3',S13]) i = i+2 tramo_usado = True # un tramo igual if (tramo_usado == False) and (i+1)<n: trapecio = (h/2)*(fi[i]+fi[i+1]) suma = suma + trapecio cuenta_h[i:i+1] = [1] # usar trapecio suma_parcial.append(['trapecio',trapecio]) i = i+1 tramo_usado = True cuenta_h[n-1] = 0 # ultima casilla if vertabla==True: #mostrar datos parciales print('Fórmulas compuestas, tramos:',n-1) print('métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado') print('tramos iguales en xi:',cuenta_h) for unparcial in suma_parcial: print('',unparcial[0],':',unparcial[1]) return(suma,cuenta_h) # PROGRAMA -------------- areaj = [] cuenta_hj = [] j = 0 # y[0] constante for j in range(0,tramosy+1,1): # cada yj print('j:',j,', yj['+str(j)+']:',yj[j]) xj = Xi[j] fj = F[j] area,cuenta_h=simpson_compuesto(xj,fj, vertabla=True, casicero=1e-7) areaj.append(area) cuenta_hj.append(cuenta_h) area,cuenta_h = simpson_compuesto(yj,areaj, vertabla=True, casicero=1e-7) # SALIDA np.set_printoptions(precision) print('xi',xi) print('yj',yj) print(titulo) print(F) print('Integral Volumen:', area)
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
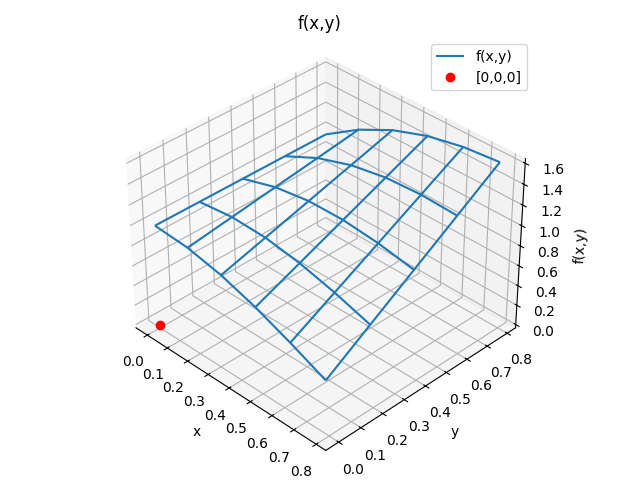
4. Gráfica de malla
Permite observar la superficie de f(x,y) sobre la que se calculará el volumen respecto al plano x,y en cero.
Instrucciones adicionales al algoritmo
# GRAFICA 3D de malla ------ import matplotlib.pyplot as plt # Malla para cada eje X,Y fig3D = plt.figure() graf3D = fig3D.add_subplot(111, projection='3d') graf3D.plot_wireframe(Xi,Yj,F,label='f(x,y)') graf3D.plot(0,0,0,'ro',label='[0,0,0]') graf3D.set_title(titulo) graf3D.set_xlabel('x') graf3D.set_ylabel('y') graf3D.set_zlabel('z') graf3D.set_title(titulo) graf3D.legend() graf3D.view_init(35, -45) plt.tight_layout() #plt.show()
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]
..
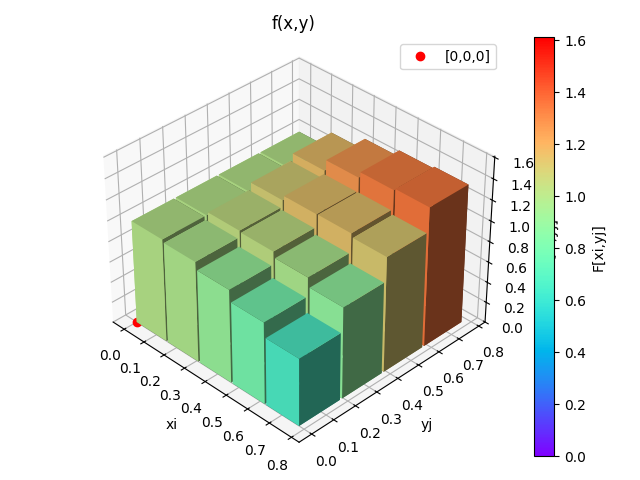
5. Gráfica de barras
Realizado para observar las barras con lados de segmentos dx=hx, dy=hy.
Instrucciones complementarias a la gráfica anterior.
# Grafica barras 3D ------ factor = 0.95 # barra proporcion dx, dy fig_3D = plt.figure() graf_3D = fig_3D.add_subplot(111,projection='3d') F_min = np.min([np.min(F),0]) F_max = np.max([np.max(F)]) color_F = F[:m-1,:n-1].ravel()/F_max color_ij = plt.cm.rainbow(color_F) graf_3D.bar3d(Xi[:m-1,:n-1].ravel(), Yj[:m-1,:n-1].ravel(), np.zeros((n-1)*(m-1)), hx*factor,hy*factor, F[:m-1,:n-1].ravel(), color=color_ij) graf_3D.plot(0,0,0,'ro',label='[0,0,0]') # escala eje z graf_3D.set_zlim(F_min,F_max) # etiqueta graf_3D.set_xlabel('xi') graf_3D.set_ylabel('yj') graf_3D.set_zlabel('z') graf_3D.set_title(titulo) graf_3D.legend() # Barra de color color_escala = plt.Normalize(F_min,F_max) color_barra = plt.cm.ScalarMappable(norm=color_escala, cmap=plt.colormaps["rainbow"]) fig_3D.colorbar(color_barra,ax=graf_3D,label="F[xi,yj]") graf_3D.view_init(35, -45) plt.tight_layout() plt.show()
[ Integral doble ] [ ejercicio ] [ algoritmo ] | gráfica: [ mallas ] [ barras ]