[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
Método de la Bisección
Referencia: Burden 2.1 p36, Chapra 5.2 p124, Rodríguez 3.1 p36
El método más simple para buscar raíces de una ecuación, se basa en el teorema del valor intermedio, búsqueda binaria, partición de intervalos o de Bolzano.
En el intervalo donde existe un cruce por cero de la función f(x), el algoritmo busca la raíz al reducir el intervalo en la mitad (bisección), seleccionando el sub- intervalo donde se mantenga el cambio de signo de la función f(x).
Los pasos a seguir son los siguientes:
- el intervalo
[a,b]se divide siempre en la mitadc. - Si la función f(x) cambia de signo sobre un intervalo, se evalúa el valor de la función en el punto medio
f(c). - La posición de la raíz se determina en el punto medio del sub-intervalo, izquierdo o derecho, dentro del cual ocurre un «cambio de signo».
- el proceso se repite hasta obtener una mejor aproximación
La gráfica muestra una animación del proceso, observe la forma en que progresivamente se acercan los puntos [a,b], donde se mantienen valores con signo diferente entre f(a) y f(b).
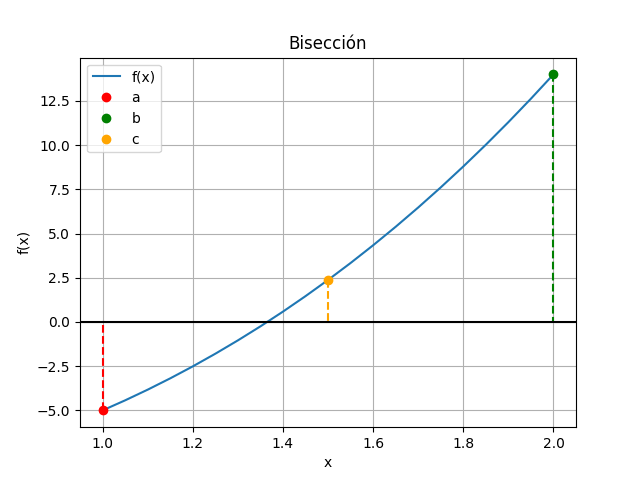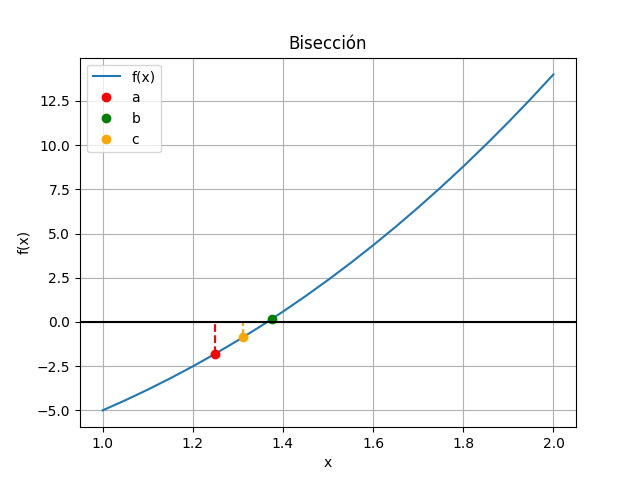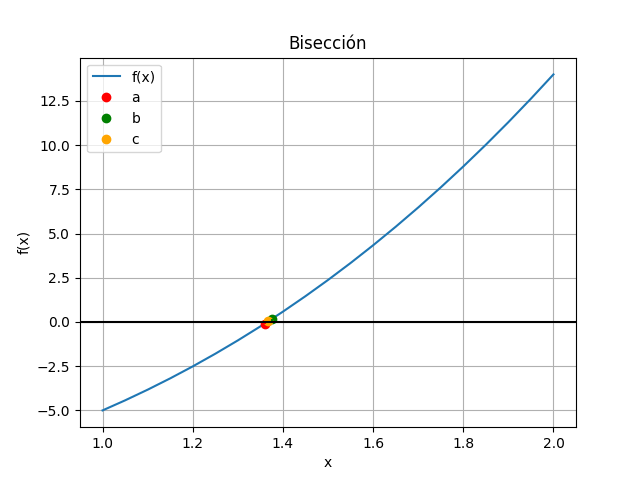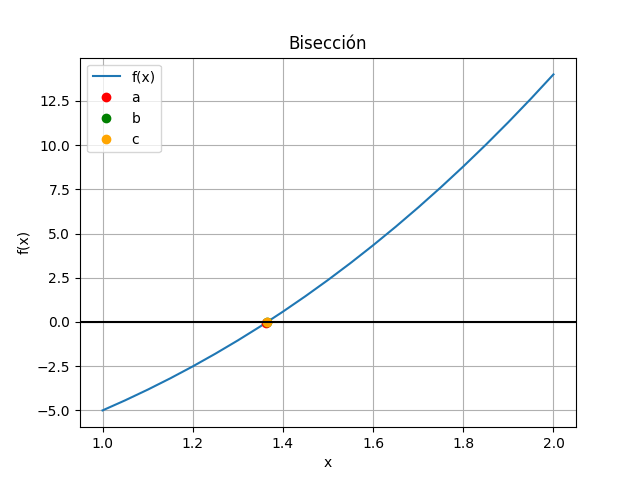
Para describir mejor el método, observamos la gráfica en una sola iteración.
Para la primera iteración se tiene que la función tiene un cambio de signo dentro del intervalo [a,b].
El intervalo se divide en la mitad, representado por el punto c, obteniendo el sub-intervalo izquierdo [a,c] o sub-intervalo derecho [c,b].
El sub-intervalo que contiene la función con un cambio de signo, se convierte en el nuevo intervalo por analizar en la siguiente iteración.
[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
Cota de Error
Referencia: Burden Teorema 2.1 p39.
El error del método de la bisección se estima como el ancho o tamaño del intervalo [a,b] de la última iteración realizada. Si el error es menor que la tolerancia del ejercicio, el algoritmo se detiene y se considera encontrada la raíz.
Suponga que f ∈ C[a,b] y f(a)*f(b)<0, f es una función en el intervalo [a,b] y que presenta un cambio de signo.
|p_n - p| \leq \frac{b-a}{2^n} \text{donde } n \geq 1la desigualdad implica que pn converge a p con una razón de convergencia de orden:
O \Big(\frac{1}{2^n}\Big)es decir:
p_n =p+O \Big( \frac{1}{2^n} \Big)Con lo que se puede determinar el número de iteraciones necesarias para encontrar la raíz, tal como se muestra en el siguiente ejercicio.
[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]
Cantidad de iteraciones – Ejercicio
Referencia: Burden ejemplo 2 p40
Determine la cantidad de iteraciones necesarias para resolver
f(x) = x^3 + 4x^2 -10 =0con exactitud de 10 – 3 en el intervalo [1,2].
Desarrollo: Se busca encontrar un entero n que satisface la ecuación:
|p_n -p| \leq \frac{b-a}{2^{n}} 2^{-n}< 10^{-3}usando logaritmos:
-n \log _{10}( 2) < -3 n > \frac{3}{\log _{10}( 2)} = 9.96En consecuencia se requieren unas diez iteraciones para lograr la aproximación de 10-3. Verifique los resultados con los valores calculados.
[ Bisección ] [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ función ]