- ►1ra Evaluación (18)
- ►1ra Eva_FIEC03236 (21)
- ►2da Evaluación (9)
- ►2da Eva_FIEC03236 (18)
- ►3ra Evaluación (9)
- ►3ra Eva_FIEC03236 (17)
- Evaluaciones
Ejercicios de evaluaciones anteriores, clasificados por temas.
3Eva_IIT2017_T5 Sistema lineal
3ra Evaluación II Término 2017-2018. Febrero 20, 2018
Tema 5. (Extra 10 puntos) Se tiene un sistema descrito con las ecuaciones y diagrama de bloques mostrados:
Y(t) = h(t)*X(t)
Z(t) = X(t) –Y(t)
a) Encuentre Rz(τ)
b) Encuentre Sz(f) en términos de Sx(f)
Rúbrica: literal a (6 puntos), literal b (4 puntos)
3Eva_IIT2017_T4 Sx(f) para QAM
3ra Evaluación II Término 2017-2018. Febrero 20, 2018
Tema 4. (25 puntos) La señal de entrada X(t) de un sistema tipo “QAM” son procesos aleatorios A(t) y B(t) independientes con densidades espectrales de potencia mostradas.
X(t) = A(t) cos(2πfct + θ) + B(t) sin(2πfct + θ)
a) Encuentre la densidad espectral de potencia de la señal QAM, SX(f)
b) Grafique su respuesta
Rúbrica: literal a (15 puntos), literal b (10 puntos)
3Eva_IIT2017_T3 Autocorrelacion AM/PM
3ra Evaluación II Término 2017-2018. Febrero 20, 2018
Tema 3 (25 puntos) Considere la combinación lineal de dos sinusoides.
X(t) = A_1 \cos (\omega _0 t + \theta _1) + A_2 \cos (\sqrt{2}\omega_0 t + \theta _2)Donde θ1 y θ2 son variables aleatorias independientes y uniformes en el intervalo (0, 2π).
A1, A2 son variables aleatorias conjuntas Gaussianas.
Asuma que las amplitudes son independientes de las variables aleatorias de la fase.
a) Encuentre la media para X(t)
b) Encuentre la función de auto-correlación para X(t)
Rúbrica: literal a (5 puntos), literal b (20 puntos)
3Eva_IIT2017_T2 Servidores Rápido y Lento
3ra Evaluación II Término 2017-2018. Febrero 20, 2018
Tema 2. (25 puntos) Considere un sistema M/M/2/2 con un servidor que opera el doble de rápido al otro.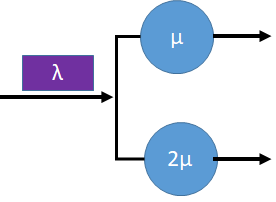 
a) ¿Cuál será la definición de “estado” para el sistema si se lo modela con una cadena de Markov continua en el tiempo?
Para cada caso, plantee el diagrama, las ecuaciones de balanceo y resuelva
b) Encuentre la pmf de estado estable para el sistema, si los clientes al llegar y encontrar los servidores libres, se los envía al servidor más rápido.
c) Encuentre la pmf de estado estable para el sistema si los clientes al llegar encuentran los servidores libres, se los envía a cualquiera con la misma probabilidad.
Rúbrica: literal a (5 puntos), literal c y d (10 puntos cada uno)
3Eva_IIT2017_T1 Radio con Respaldo
3ra Evaluación II Término 2017-2018. Febrero 20, 2018
Tema 1. (25 puntos) Un sistema de radio transmisión unidireccional con respaldo, semejante a maquinaria de doble uso, tiene dos partes A y B.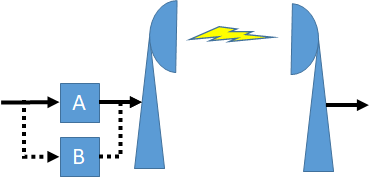 
El sistema se mantiene operando solo con una de las dos partes, la otra es de respaldo.
Cualquiera de las partes en operación falla cualquier día con probabilidad a.
Una parte dañada se repara el siguiente día con probabilidad b. 
Los eventos de falla y reparación son independientes.
Sea Xn el número de partes funcionando en el día n.
a) Desarrolle un modelo de cadena de Markov usando tres estados (diagrama).
b) Determine la matriz de transición P de un paso usando las variables a, b. Justifique las ecuaciones usadas
c) Usando P y con a=0.1 y b=0.7, encuentre la función de probabilidad de masa de estado estable. (desarrollar).
d) ¿Podría determinar la pmf de estado estable si tuviese n usos o partes? Esquema y explique.
Rúbrica: literal a, estados, diagrama (5 puntos), literal b (10 puntos), literal c(6 puntos), literal d (4 puntos)
2Eva_IIT2017_T4 Sy(f) con funcion de transferencia H(f)
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 4 (15 puntos). La entrada a un filtro es un ruido blanco con media cero y densidad espectral de potencia N0/2.
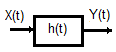El filtro tiene la función de transferencia mostrada:
a) Encuentre SY,X(f) y RY,X(τ)
b) Encuentre SY(f) y RY(τ)
c) Calcule la potencia promedio del proceso de salida
Rúbrica: literal a (6 puntos), literal b (6 puntos), literal c (3 puntos)
2Eva_IIT2017_T3 Sy(f) de la correlación Rx(t)
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 3. (15 puntos) Encuentre la densidad espectral de potencia SY(f) de un proceso aleatorio con función de auto-correlación:
RX(τ) cos(2 π f0 τ)
donde RX(τ) es en si mismo una función de auto-correlación.
Determine la potencia promedio, si RX(τ) es de tipo triangular y grafique Sy(f).
Rúbrica: Sy(f) (5 puntos), potencia promedio (5 puntos) Sy(f) nueva(5 puntos)
2Eva_IIT2017_T2 Covarianza XY
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 2. (45 puntos) Sean X(t) y Y(t) mostrados en la figura, donde θ es una variable aleatoria uniforme, distribuida en el rango [-π π].
X(t) = \cos (\omega t + \theta) Y(t) = \sin (\omega t + \theta)Como ejemplo, si ω = 1/2, para θ = 0 y θ = π/4, se muestran los resultados en la figura sobre X(t) y Y(t).
Determine los resultados para:
a) Valor esperado de X(t)
b) Valor esperado de Y(t)
c) Correlación cruzada entre X(t) y Y(t)
d) Covarianza cruzada de X(t) y Y(t)
e) Determinar si el proceso Y es estacionario o estacionario en el sentido amplio. Justifique su respuesta
Rúbrica: literal a y b (5 puntos cada uno), literal c (20 puntos), literal d (5 puntos), literal e) (10 puntos)
2Eva_IIT2017_T1 PDF exp(ax)
2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 1 (25 puntos). Sea Y una variable aleatoria definida por: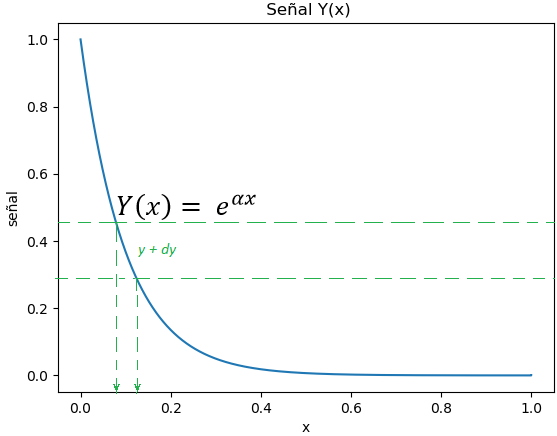
donde X es una variable aleatoria uniforme, distribuida en el intervalo
de (0, T ]
a) Determine la función densidad de probabilidad para Y
b) Calcule la función de distribución acumulada para Y
c) Grafique su resultado
d) Determine la auto-correlación para Y
Rúbrica: literal a (10 puntos), literal b, c, d (5 puntos cada uno)