En áreas extensas de medición donde existen diferentes ambientes o entornos como vegetación en una parte y edificios en otros, el resultado de básico de un solo intervalo puede mejorarse al utilizar subintervalos para cada entorno.
El cambio de entorno forma una frontera, observando la distancia al gateway (baliza) se la toma el valor como punto de partida para estimar la linealización de cada sub-intervalo. Se determinan las ecuaciones para cada intervalo, para calcular los puntos de intersección de cada linea teniendo como resultado una frontera entre diferentes ambientes calculada a partir de las mediciones realizadas.
baliza: ‘gtwFIEC’
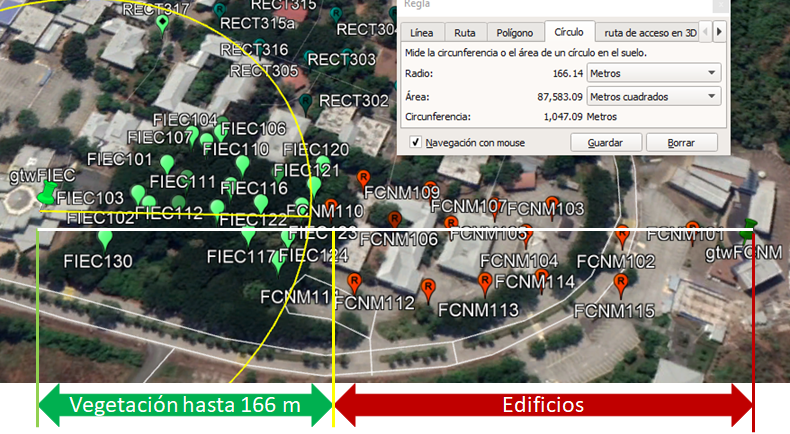
Por ejemplo, para ‘gtwFIEC’ y su entorno mostrado en la imagen, en los puntos cercanos existe un ambiente con principalmente vegetación, que luego en puntos más alejados hay ambientes urbanos con edificios de aulas y administrativos.
Partiendo del ‘gtwFIEC’ se estima una frontera inicial a 176 metros para usar dos subintervalos y realizar la linealización.
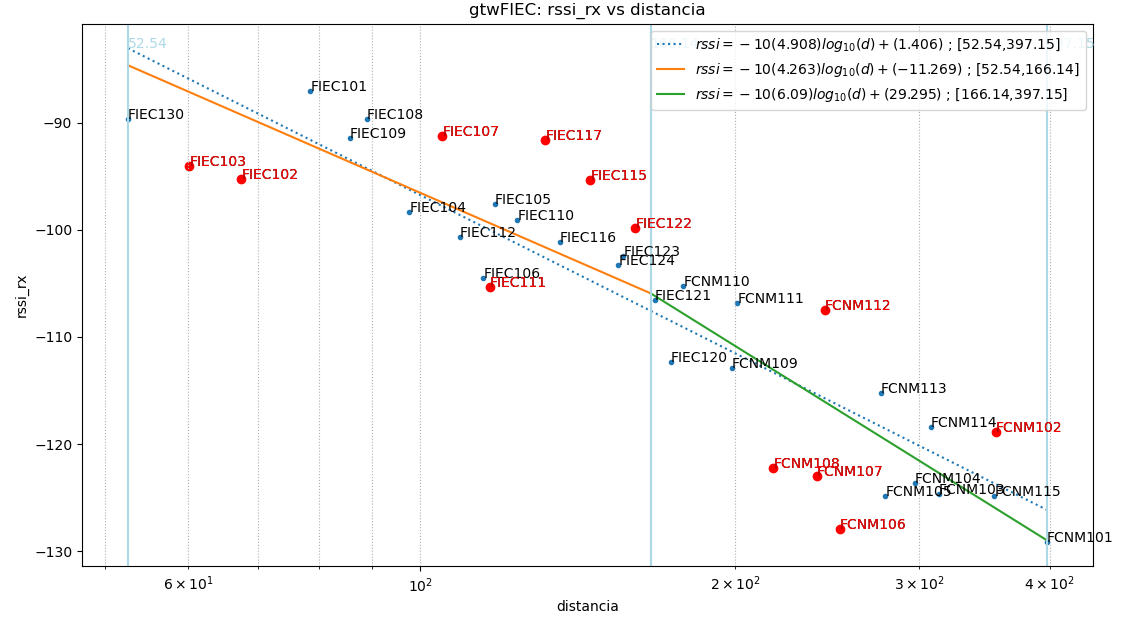
Los resultados que se obtienen son:
Un intervalo
Rssi(d) = -10(4.908)log_{10}(d)+1.406 52.54 \le d \le 397.15|error_rssi| promedio: 4.84 , std: 5.56
|error_dist| promedio: 41.43 , std: 54.09
Dos intervalos
Rssi_0(d) = -10(4.263)log_{10}(d)+(-11.269) 52.54 \le d \le 166.14|error_rssi| promedio: 2.92 , std: 3.33
|error_dist| promedio: 20.19 , std: 24.67
Rssi_1(d) = -10(6.09)log_{10}(d)+(29.295) 166.14 \le d \le 397.15|error_rssi| promedio: 2.71 , std: 3.17
|error_dist| promedio: 25.03 , std: 29.93
baliza: ‘gtwFCNM’
Para el caso ‘gtwFCNM’ el área de interés con vegetación se encuentra a partir de los 230 metros, tomado como valor inicial de frontera.
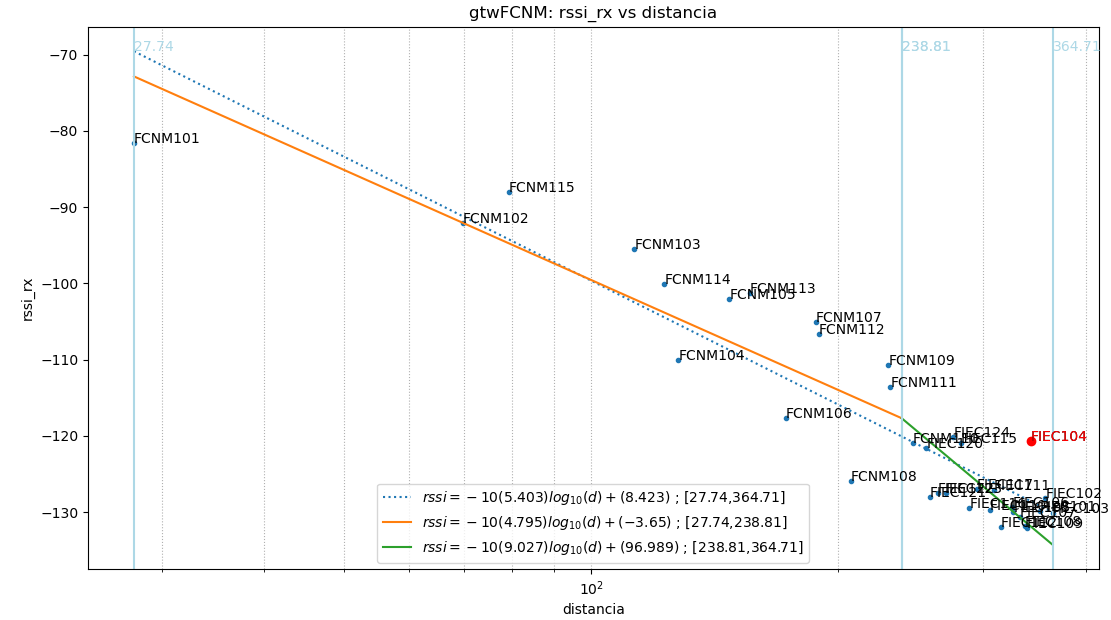
Un intervalo
Rssi(d) = -10(5.403)log_{10}(d)+(8.423)
27.74 \le d \le 364.71
|error_rssi| promedio: 4.59 , std: 5.48
|error_dist| promedio: 41.33 , std: 48.24
Dos intervalos
Rssi_0(d) = -10(4.795)log_{10}(d)+(-3.65) 27.74 \le d \le 238.81|error_rssi| promedio: 5.96 std: 6.51
|error_dist| promedio: 52.15 , std: 64.38
Rssi_1(d) = -10(9.027)log_{10}(d)+(96.989) 238.81 \le d \le 364.71|error_rssi| promedio: 2.81 , std: 3.43
|error_dist| promedio: 20.26 , std: 25.06
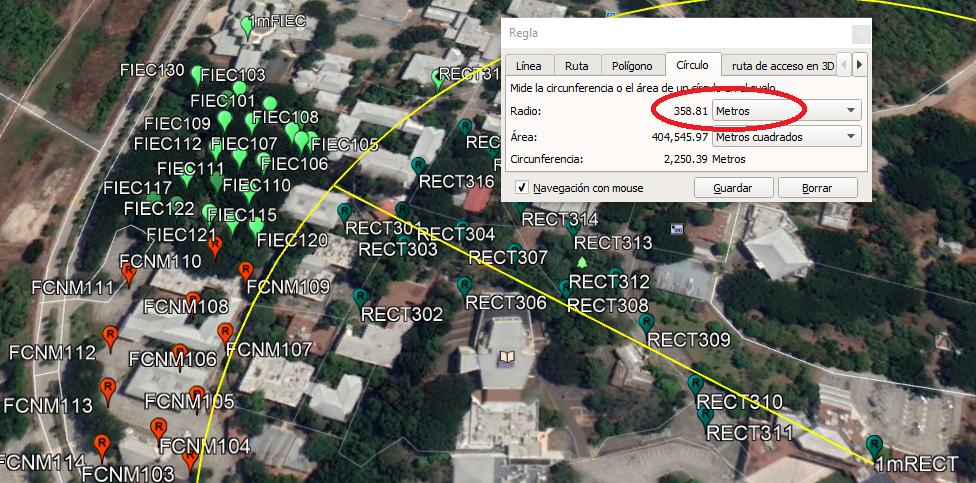
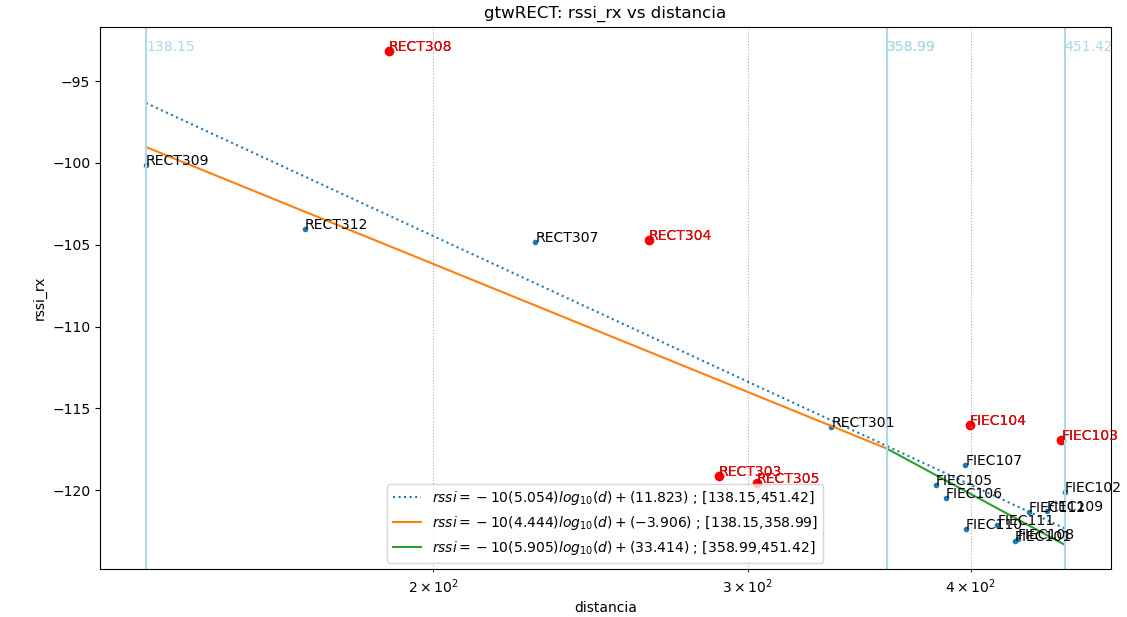
baliza: ‘gtwRECT’
Un intervalo
Rssi(d) = -10(5.054)log_{10}(d)+(11.823) 138.15 \le d \le 451.42|error_rssi| promedio: 3.11 , std: 3.97
|error_dist| promedio: 42.93 , std: 51.69
Dos intervalos
Rssi_0(d) = -10(4.4443)log_{10}(d)+(-3.906) 138.15 \le d \le 358.99|error_rssi| promedio: 1.38 , std: 1.77
|error_dist| promedio: 18.99 , std: 23.13
Rssi_1(d) = -10(5.905)log_{10}(d)+(33.414) 358.99 \le d \le 451.42|error_rssi| promedio: 1.35 , std: 1.53
|error_dist| promedio: 21.17 , std: 24.68
Parámetros
Los parámetros para el algoritmo se establecen en el diccionario ‘analiza’. frontera es el vector donde se indica los puntos de corte del intervalo bajo estudio. Si frontera es vacio [], se asume que se analiza todo el intervalo.
Los parámetros usados en el algoritmo para obtener los resultados presentados corresponden a:
# Analizar por segmentos analiza = {'gtwRECT':{'analizar' : 1, 'atipico_std' : 1, 'frontera' : [320], 'atipInterv_std': [1,1], 'p_amplia': 4, 'grp' : ['RECT','FIEC'], 'tip' : ['punto'], 'LOS' : [1]}, 'gtwFIEC':{'analizar' : 1, 'atipico_std' : 1, 'frontera' : [190], 'atipInterv_std': [1,1], 'p_amplia': 4, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [1,0]}, 'gtwFCNM':{'analizar' : 1, 'atipico_std' : 1, 'frontera' : [235.0], 'atipInterv_std': [2,2], 'p_amplia': 4, 'grp' : ['FIEC','FCNM'], 'tip' : ['punto'], 'LOS' : [1,0]} }
En la siguiente sección se detalla el algoritmo usado para generar las ecuaciones en cada segmento, las ecuaciones son usadas para estimar la ubicación relativa a cada baliza.