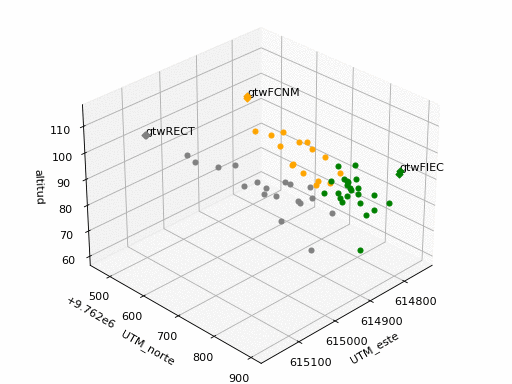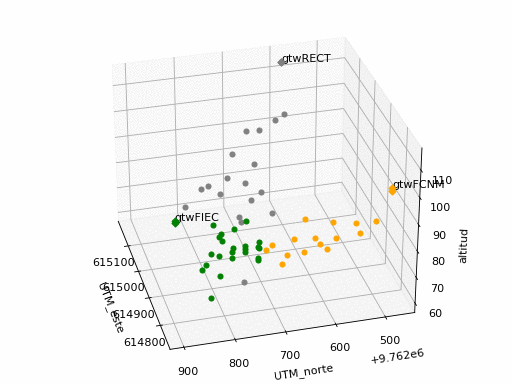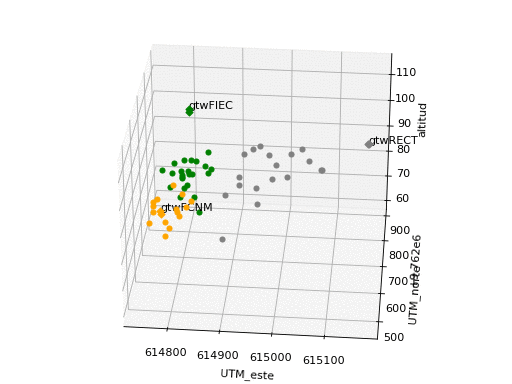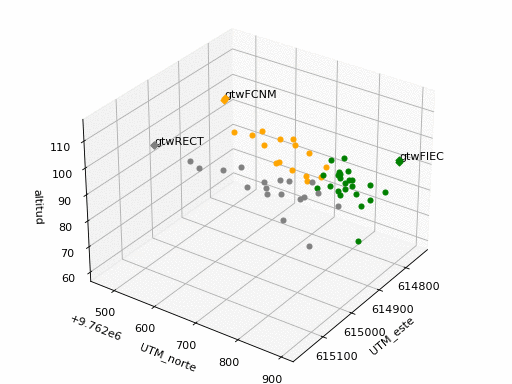
Referencia: Chapra 17.1 p 466. Burden 8.1 p498, Mínimos cuadrados en Métodos numéricos
La linealización de curvas con Método de mínimos cuadrados se realiza usando las funciones de Numpy: np.linalg.lstsq()
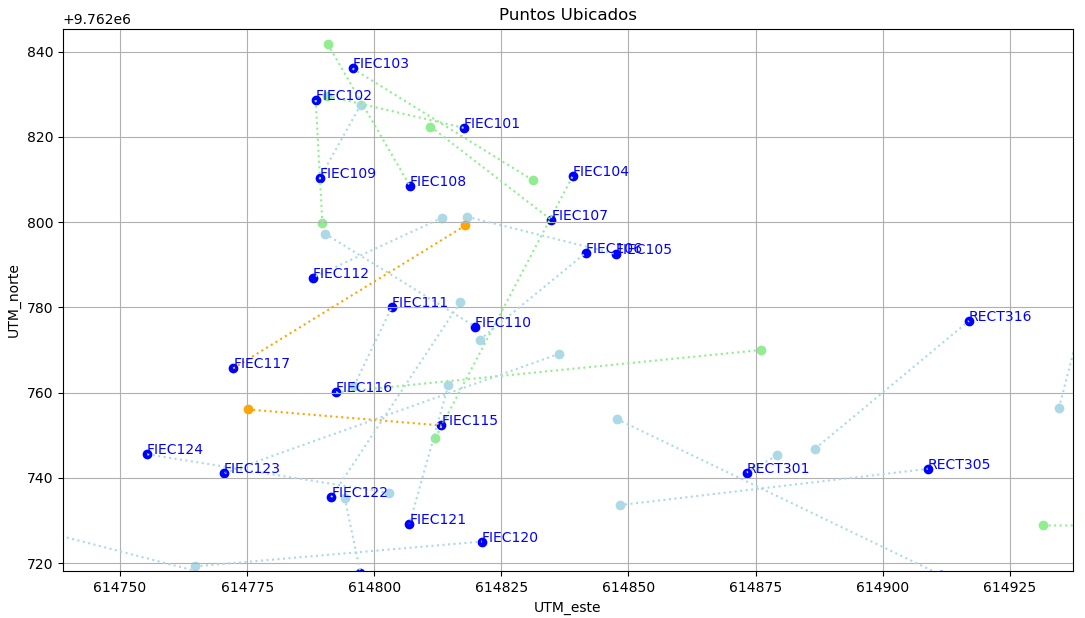
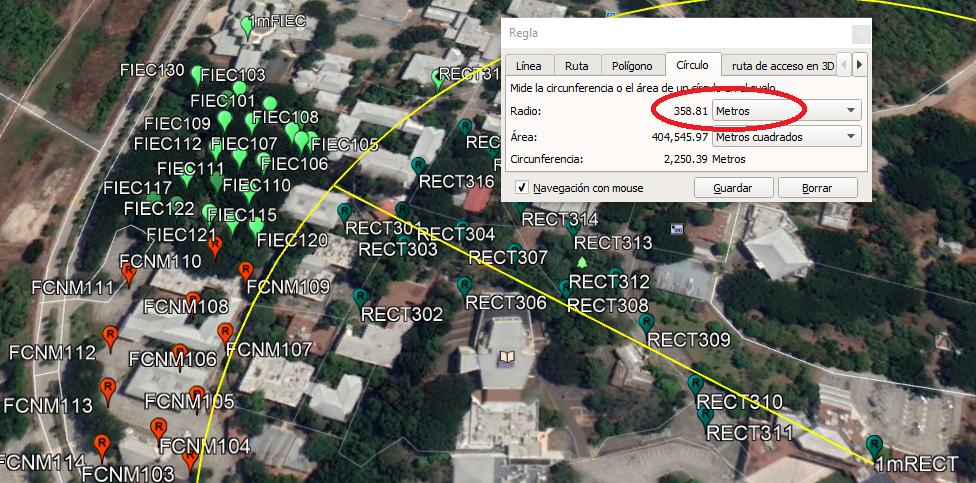
Para el análisis de una baliza, 'gtwFIEC', se obtienen los datos desde el archivo 'resumen_RssiUbica01' obtenido en:
Integrar las tablas de Rssi y coordenadas de los puntos
entregando como resultado un archivo con las ecuaciones obtenidas: 'resumen_ecuacionSimple05.json'
La selección de la baliza se realiza con un diccionario indicando la acción de 'analizar' como verdadero o falso (1,0), entre otros parámetros.
'gtwFIEC':{'analizar' : 1,
'atipico_std' : 1,
'grp' : ['FIEC','FCNM'],
'tip' : ['punto'],
'LOS' : [1,0]}
Los valores atípicos se los discrimina a partir de la desviación estándar, indicando el número de veces que se la considera como medida de dispersión.

Los puntos identificados en cada sector se seleccionan en 'grp': FIEC, FCNM, RECT.
El tipo de medición tomada, 'tip', se identifica por: punto, 1m, gtw, dispositivo.
Un parámetro auxiliar es 'LOS', que indica los puntos seleccionados con Línea de vista (1) y sin linea de vista (0). Para incluir todos de debe ingrear [1,0]. Este parametro se puede modificar en el archivo de entrada: arch_medidaubica.
Los datos de cada eje se seleccionan mediante la función pares_usar(tabla, baliza, analiza, unabaliza, medida, modo) que entrega como resultado los arreglos de pares ordenados y las etiquetas con los nombres, par_etiqueta).
La linealización se realiza con el método de los mínimos cuadrados, con lo que se establece el |error| promedio y desviación estándar.
|error| = |yi - f(xi)|
|error_{medio}| = \frac{1}{n}\sum|yi - f(xi)|
Procedimiento aplicado
Para el análisis primero se consideran todos los puntos disponibles para obtener la primera ecuación, mostrada en el ejemplo con la línea azul.
Con ésto es posible determinar un error de estimación, para luego proceder a discriminar los puntos atípicos.
Se realiza una nueva estimación de linealización habiendo discriminado los puntos atípicos y se observa el resultado.
Resultados para baliza: gtwFIEC
El resultado del algoritmo se presenta como gráfica, en pantalla y un archivo con los datos de las fórmulas.
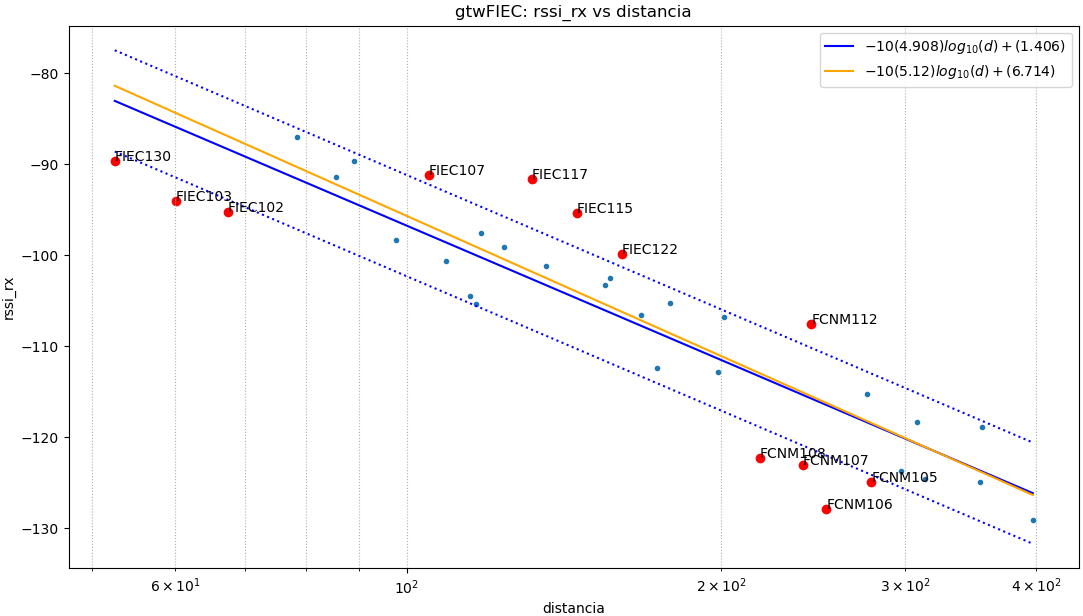
los resultados se pueden observar en lo mostrado.:
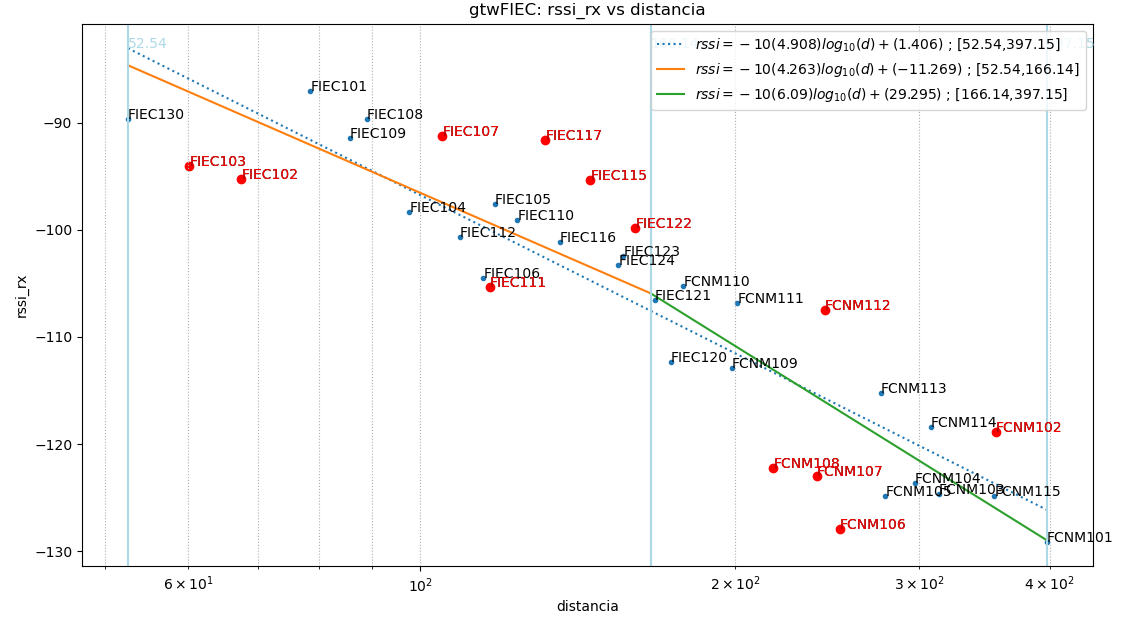
baliza: gtwFIEC
Puntos usados: todos
$ -10(4.908).log_{10}(d)+(1.406)$
|error| promedio: 4.84 , std: 5.56
Puntos usados: NoAtipico
$ -10(5.12).log_{10}(d)+(6.714)$
|error| promedio: 2.98 , std: 3.31
>>>
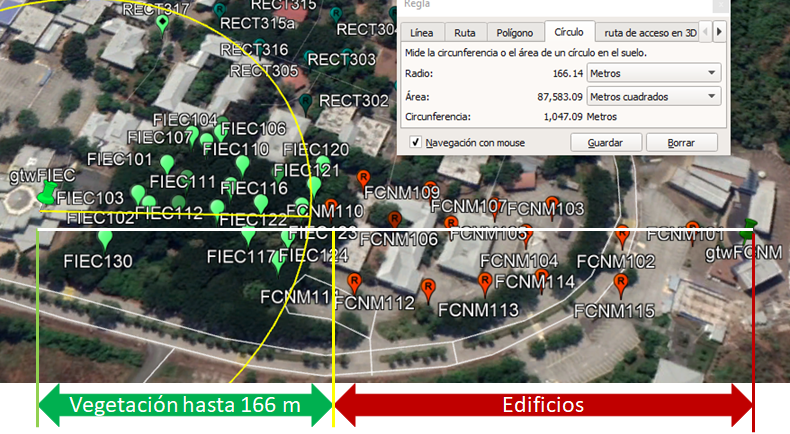
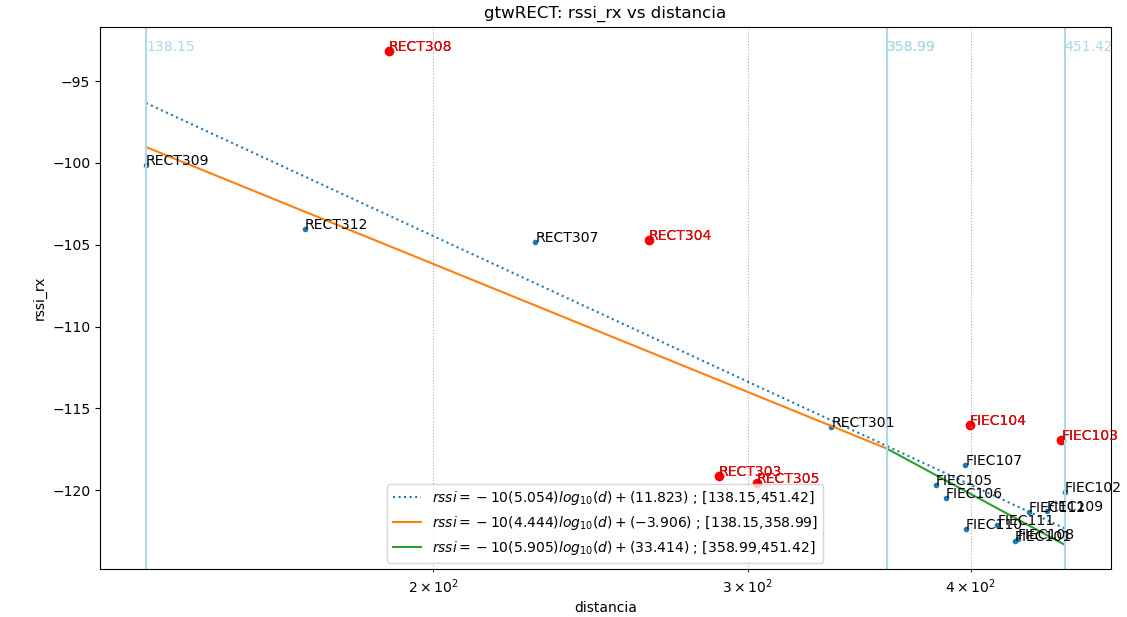
Se observa que los valores fuera de la banda de valores con una desviación estándar (σ) se muestran distruidos en tres grupos: dos grupos a la izquierda y derecha de la gráfica por debajo de la banda y un grupo en el centro por sobre la banda.
Se considera explorar la división del intervalo en dos, puesto que existen dos entornos: uno principalmente conformado con vegetación y otro con edificaciones.
los resultados que se van al archivo, incluyen todos los decimales:
exportar resultados :
{'todos': {'intervalox': [52.543, 397.148],
'intervaloy': [-129.132183908046, -86.98969072164948],
'alpha': 4.907571379870146, 'beta': 1.4062384027235748,
'error_medio': 4.840153103044936, 'error_std': 5.562835152792785,
'eq_latex': '$ -10(4.908).log_{10}(d)+(1.406)$'
},
'NoAtipico': {'intervalox': [78.492, 397.148],
'intervaloy': [-129.132183908046, -86.98969072164948],
'alpha': 5.119532447831607, 'beta': 6.713572849706863,
'error_medio': 2.9780010745912833, 'error_std': 3.312804227070313,
'eq_latex': '$ -10(5.12).log_{10}(d)+(6.714)$'
}
}
Para revisar la situación se presentan los resultados con otra baliza.
Baliza: gtwFCNM
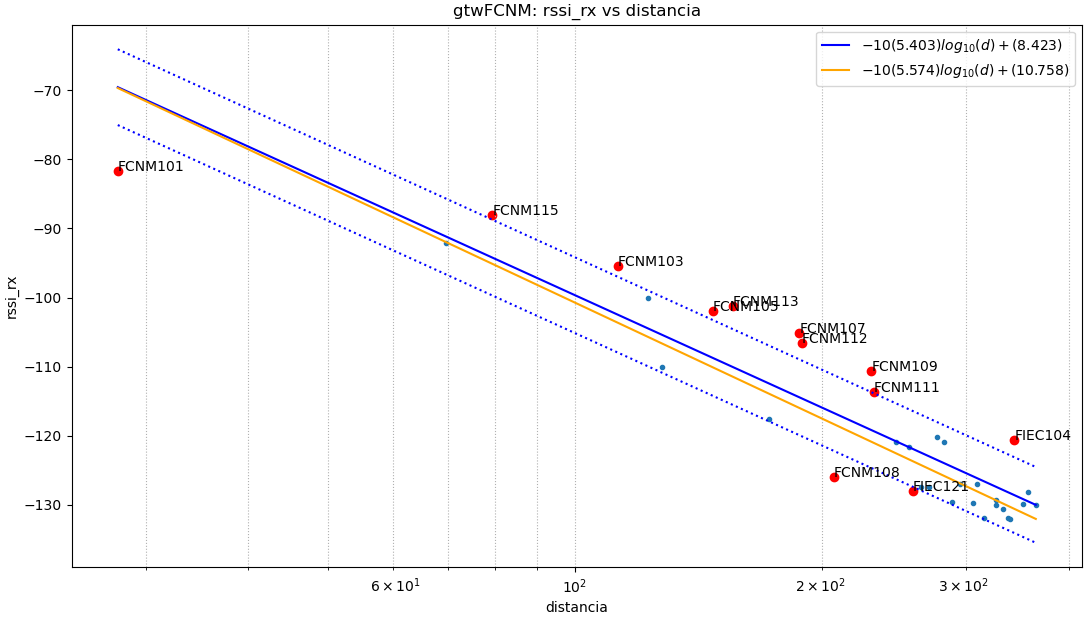
Resultados del algoritmo.
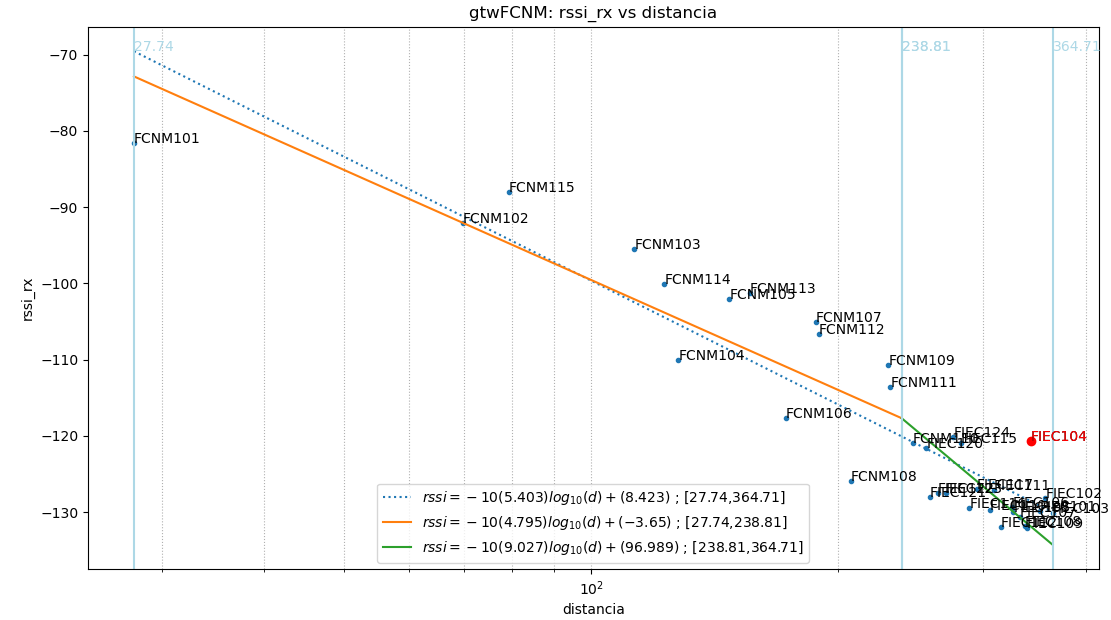
baliza: gtwFCNM
Puntos usados: todos
$ -10(5.403).log_{10}(d)+(8.423)$
|error| promedio: 4.59 , std: 5.48
Puntos usados: NoAtipico
$ -10(5.574).log_{10}(d)+(10.758)$
|error| promedio: 2.31 , std: 2.79
Baliza: gtwRECT
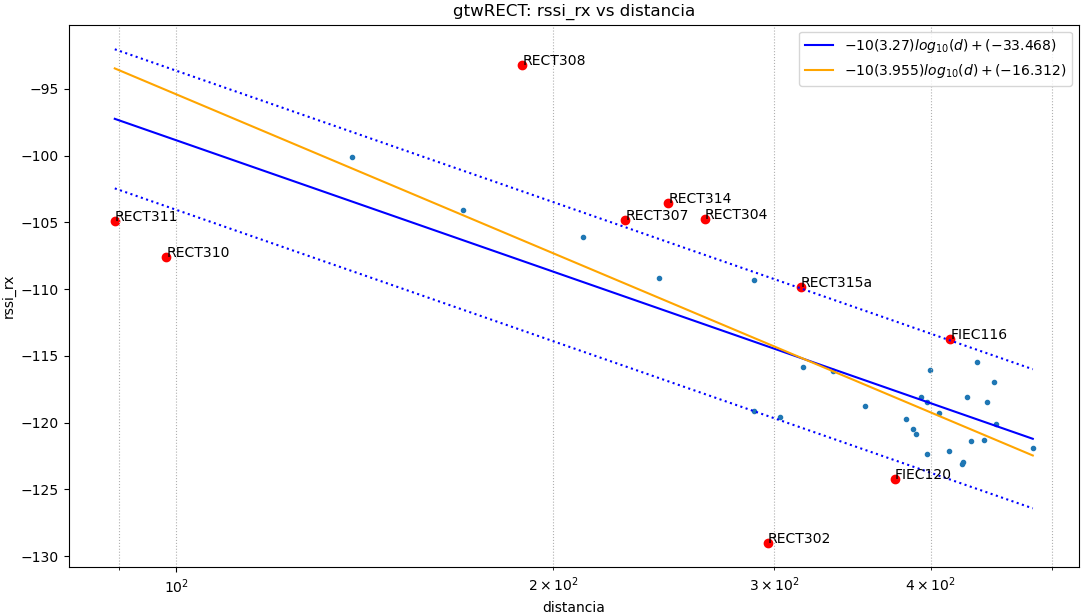
baliza: gtwRECT
Puntos usados: todos
$ -10(4.89).log_{10}(d)+(8.541)$
|error| promedio: 2.9 , std: 3.73
Puntos usados: NoAtipico
$ -10(4.587).log_{10}(d)+(0.326)$
|error| promedio: 1.41 , std: 1.72
Algoritmo en Python
El algoritmo realiza el proceso de datos para cada baliza usando los datos del archivo "resumen_rssiUbica01.txt", que el el resultado del proceso realizado en Integrar las tablas de Rssi y coordenadas de los puntos
Los resultados del algoritmo se almacenan en el archivo "arch_ecuaciones".
Los parámetros para el análisis se incorporan en el diccionario "analiza". Los parámetros se describen al inicio de la página.
Como el proceso de linealización se reutiliza, se lo incorpora como parte de la librería girni_lora_libreria, sin embargo la función se describe en detalle en Rssi(distancia) Linealización - función Python .
Procedimiento
Los datos se leen desde el archivo y se incorporan a una estructura de datos en Pandas.
Para cada baliza se determina si se ha indicado 'analizar', con lo que se seleccionan los pares ordenados y etiquetas a usar mediante la función girni.pares_usar().
Con los datos seleccionados, se aplica mínimos cuadrados y se obtienen los errores mediante la función girni.linealiza_lstsq(). Mediante el criterio de desviación estándar se discriminan los datos atípicos y se vuelve a evaluar los datos sin atipicos, entregando el resultado mediante archivos y gráficas.
# LoRa-Multipunto, Rssi vs distancia
# linealización Rssi vs log10(distancia)
# por mínimos cuadrados, Graficas 2D y 3D
# Girni 2020-10-07 propuesta: edelros@espol.edu.ec
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import girni_lora_libreria as girni
# INGRESO
# archivos de entrada
modo = 'rx'
medida = 'rssi'
arch_medidaubica = 'resumen_rssiUbica01.txt'
# archivos de salida
arch_ecuaciones = 'resumen_ecuacionSimple05.json'
analiza = {'gtwRECT':{'analizar' : 1,
'atipico_std' : 1,
'grp' : ['FIEC','RECT'],
'tip' : ['punto'],
'LOS' : [1,0]},
'gtwFIEC':{'analizar' : 1,
'atipico_std' : 1,
'grp' : ['FIEC','FCNM'],
'tip' : ['punto'],
'LOS' : [1,0]},
'gtwFCNM':{'analizar' : 1,
'atipico_std' : 1,
'grp' : ['FIEC','FCNM'],
'tip' : ['punto'],
'LOS' : [1,0]}
}
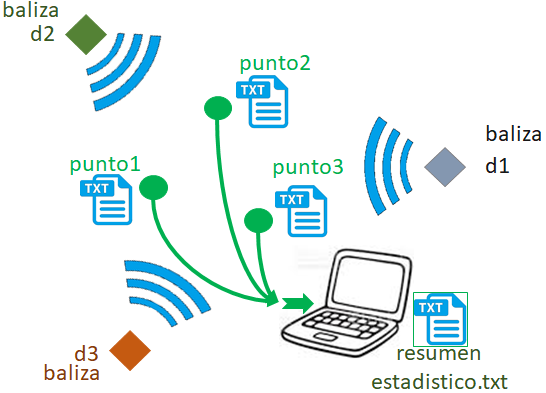
baliza = {'d1':'gtwRECT',
'd2':'gtwFIEC',
'd3':'gtwFCNM'}
# Parámetros de grafica
tipograf = '2D' # '2D','3D'
escala = 'log' # 'normal','log'
escalabase = 10 # 10, np.exp()
# PROCEDIMIENTO
# Resultados de análisis
ecuacion = {}
eq_graf = {}
# leer datos
tabla = pd.read_csv(arch_medidaubica, index_col='etiqueta')
tabla = pd.DataFrame(tabla)
# Analizar datos hacia una baliza
for unabaliza in analiza:
# Parámetros
analizar = analiza[unabaliza]['analizar']
atipico_std = analiza[unabaliza]['atipico_std']
if analizar:
ecuacion[unabaliza] ={}
eq_graf[unabaliza] = {}
# pares a usar
[pares,par_etiqueta] = girni.pares_usar(tabla,baliza,
analiza,unabaliza,
medida,modo)
# analiza puntos para mínimos cuadrados
xi = pares[:,0]
yi = pares[:,1]
ecuacion0 = girni.linealiza_lstsq(xi,yi)
fdist0 = ecuacion0['eq_lambda']
yi0 = fdist0(xi)
# Selecciona atipicos
dyi0std = ecuacion0['error_std']
dyi0 = yi - yi0
atipicos = np.abs(dyi0) >= dyi0std*atipico_std
xi0_e = xi[atipicos]
yi0_e = yi[atipicos]
etiq0_e = par_etiqueta[atipicos]
# datos sin atipicos ----------
atipicoNo = np.abs(dyi0) <= dyi0std*atipico_std
xi1 = xi[atipicoNo]
yi1 = yi[atipicoNo]
etiq1 = par_etiqueta[atipicoNo]
ecuacion1 = girni.linealiza_lstsq(xi1,yi1)
fdist1 = ecuacion1['eq_lambda']
yi1 = fdist1(xi)
# para exportar
ecuacion[unabaliza] = {'todos': ecuacion0,
'NoAtipico': ecuacion1
}
eq_graf[unabaliza] = {'puntos': [xi,yi],
'todos' : yi0,
'atipicos':[xi0_e,yi0_e],
'atip_etiq': etiq0_e,
'NoAtipico':yi1
}
# SALIDA
for unabaliza in ecuacion:
print('baliza: ',unabaliza)
for unaecuacion in ecuacion[unabaliza]:
error_medio = ecuacion[unabaliza][unaecuacion]['error_medio']
error_std = ecuacion[unabaliza][unaecuacion]['error_std']
print('Puntos usados:', unaecuacion)
print(ecuacion[unabaliza][unaecuacion]['eq_latex'])
print('|error| promedio: ',np.round(error_medio,2),
' , std:',np.round(error_std,2))
print('\n',ecuacion[unabaliza],'\n')
print()
# salida a archivo
ecuacion = pd.DataFrame.from_dict(ecuacion)
ecuacion.to_json(arch_ecuaciones)
# GRAFICAR
# Referencias para gráfica
grupo = ['FIEC' ,'FCNM' ,'RECT','CIRC']
colores = ['green','orange','grey','magenta']
tipo = ['punto','1m' ,'gtw','dispositivo']
marcas = [ 'o','D' ,'D' ,'*' ]
mostrargrpeti = ['FIEC','FCNM','RECT']
mostrartipeti = ['1m','gtw']
for unabaliza in ecuacion:
figura,grafica = plt.subplots()
if escala == 'log':
grafica.set_xscale(escala,base=escalabase)
# todos los puntos
[xi, yi] = eq_graf[unabaliza]['puntos']
grafica.scatter(xi,yi,marker='.')
fdtxt = ecuacion[unabaliza]['todos']['eq_latex']
# linea con todos los puntos
yi0 = eq_graf[unabaliza]['todos']
grafica.plot(xi,yi0,color='blue', label = fdtxt)
[xi0_e,yi0_e] = eq_graf[unabaliza]['atipicos']
etiq0_e = eq_graf[unabaliza]['atip_etiq']
# cotas de error
atipico_std = analiza[unabaliza]['atipico_std']
dyi0std = ecuacion[unabaliza]['todos']['error_std']
grafica.plot(xi,yi0 + dyi0std*atipico_std,
color='blue',linestyle='dotted')
grafica.plot(xi,yi0 - dyi0std*atipico_std,
color='blue',linestyle='dotted')
# atipicos
grafica.scatter(xi0_e,yi0_e, color='red')
# atipicos etiquetas
m = len(xi0_e)
for i in range(0,m,1):
grafica.annotate(etiq0_e[i],
(xi0_e[i],yi0_e[i]),)
# linea Sin Atipicos
yi1 = eq_graf[unabaliza]['NoAtipico']
fdtxt1 = ecuacion[unabaliza]['NoAtipico']['eq_latex']
grafica.plot(xi,yi1, color='orange', label = fdtxt1)
# etiquetas y títulos
grafica.legend()
grafica.set_ylabel(medida+'_'+modo)
grafica.set_xlabel('distancia')
untitulo = unabaliza+': '+medida+'_'+modo + ' vs distancia'
grafica.set_title(untitulo)
grafica.grid(True,linestyle='dotted',
axis='x', which='both')
plt.show()