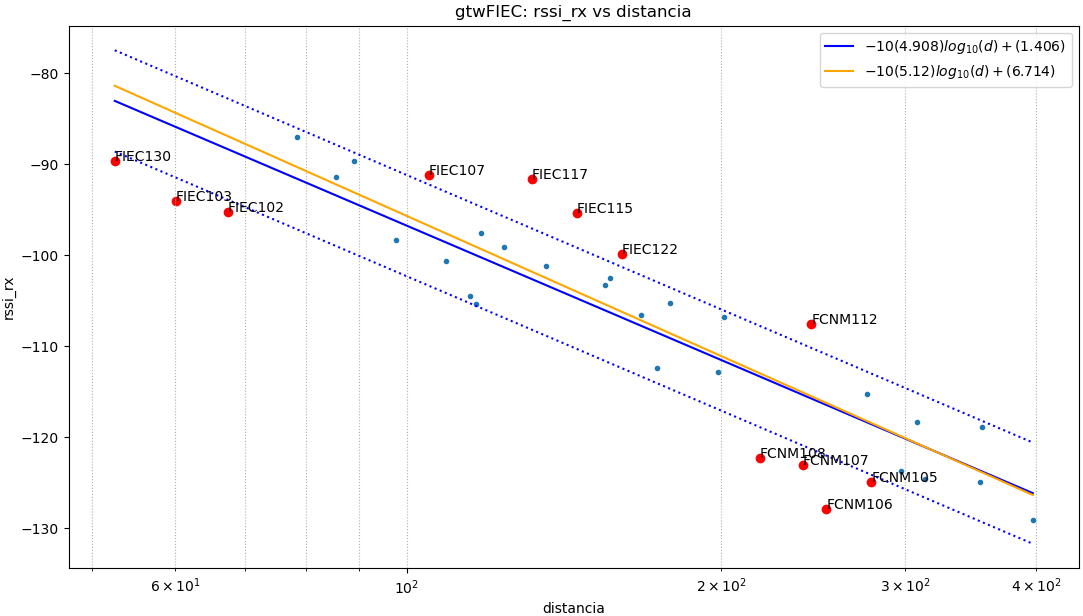
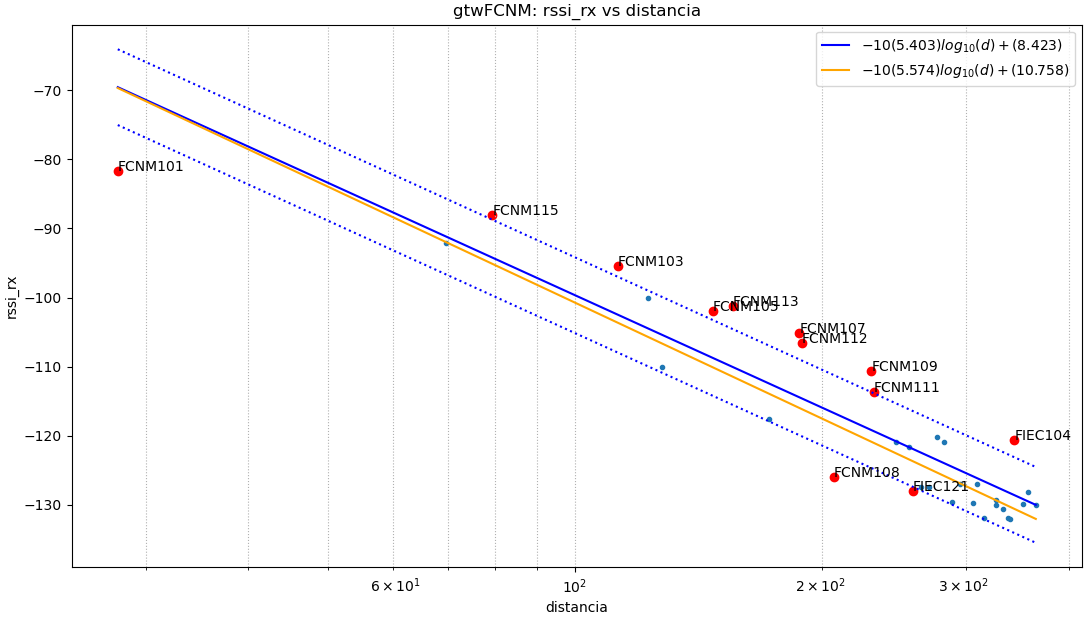
La relación de Rssi y distancia se puede observar usando los puntos en una gráfica 2D. El modelo teórico básico de larelación en espacio libre considera linealizar usando log10(distancia) para el eje x.
Método Empírico para ecuación Rssi(distancia)
La ecuación empírica con la que se realiza la primera estimación se modela como:
RSSI(d) = -10 \alpha \log_{10} (d) + P_{0} 1<d<L1. Gráfica de todos los puntos en gtwFIEC
Para observar el resultado integral de todos los puntos medidos en las áreas de vegetación de FIEC y edificios FCNM realiza un primer modelo de linealización con todos los puntos. Para el eje x se usa log10(d)
Como ejemplo se presenta la gráfica para la baliza ‘d2’ etiquetada como gtwFIEC.
La linealización se realiza usando el método de los mínimos cuadrados (least square).
Al tomar como cota de error una desviación estándar por encima y por debajo de la línealización, se pueden discriminar los datos más alejados como atípicos. Se puede realizar nuevamente la linealización sin considerar los datos atípicos resultando un aumento en el valor de la pendiente α.
Al observar los datos de la gráfica que se encuentran fuera de la banda de una desviación estándar (σ) se tiene que se encuentran distribuidos en grupos: izquierda, centro y derecha. La observación lleva a considerar usar dos intervalos para realizar linealización, que es acorde los entornos de medición; los primeros puntos con etiqueta FIEC se realizaron en zona de vegetación, y los etiquetados como FCNM se realizaron en zona de edificios de aulas y administrativos.
El análisis de los datos se divide en dos secciones:
- Análisis con un solo entorno, un intervalo para eje distancia
- Análisis con dos entornos, dos intervalos para eje distancia