Definición. Sean V y W espacios vectoriales cualesquiera. Una transformación lineal T{:}\ V\rightarrow W es una función que asigna a cada vector v\in V un vector único T(v)\in W y que satisface las siguientes condiciones: 1) \forall\ v_1, v_2\in V{:}\ T(v_1+v_2)=T(v_1)+T(v_2). 2) \forall\ v\in V,\ \forall \alpha\in \mathbb{R}{:}\ T(\alpha v)=\alpha T(v).
Ejemplo. Sean V=\mathbb{C}[a,b] y W=\mathbb{R} espacios vectoriales. Demuestre que la transformación T{:}\ V\rightarrow W definida por T(f)=\int_{a}^{b} f(x) dx es lineal.
Solución.
1) \forall\ f, g\in V{:}\ T(f+g)=T(f)+T(g).
\small{T(f)=\int_{a}^{b} f(x) dx \qquad T(g)=\int_{a}^{b} g(x) dx \qquad (f+g)(x)=f(x)+g(x)}\begin{array}{rcl}T(f+g)&=&\int_{a}^{b} (f+g)(x)dx\\T(f+g)&=&\int_{a}^{b} [f(x)+g(x)]dx\\T(f)+T(g)&=&\int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx\end{array}
2) \forall\ f\in V,\ \forall \alpha\in \mathbb{R}{:}\ T(\alpha f)=\alpha T(f)
\small{(\alpha f)(x)=\alpha f(x) \qquad T(f)=\int_{a}^{b} f(x) dx \Longrightarrow T(\alpha f)=\int_{a}^{b} (\alpha f)(x) dx}\small{\int_{a}^{b} (\alpha f)(x) dx = \int_{a}^{b} \alpha f(x) dx = \alpha \int_{a}^{b} f(x) dx = \alpha T(f)}
Por consiguiente, T{:}\ V\rightarrow W es una transformación lineal.
Teorema. Sea T{:}\ V\rightarrow W una transformación lineal entonces: La imagen del cero vector de V es el cero vector de W. T(0_V)=0_W La imagen del inverso de V es el inverso de V. T(-v)=-T(v) La transformada de la combinación lineal es la combinación lineal de la transformada. \small{T(\alpha_1 V_1 + \alpha_2 V_2 + ... +\alpha_n V_n)=\alpha_1 T(V_1) + \alpha_2 T(V_2) + ... +\alpha_n T(V_n)}
Ejemplo. Sea T{:}\ \wp_2 \rightarrow \mathbb{R^3} una tranformación lineal tal que:\footnotesize{T(x+1)=\left(\begin{array}{r} 1 \\ 0\\ 1 \end{array}\right) \quad T(x^2 -1)=\left(\begin{array}{r} 0 \\ 1\\ 1 \end{array}\right) \quad T(2x^2+x-2)=\left(\begin{array}{r} 1 \\ 1\\ 0 \end{array}\right)}Determine T(ax^2+bx+c).
Solución.
T(ax^2+bx+c)=aT(x^2)+bT(x)+cT(1)
\left\{ \begin{array}{rcl}T(x)+T(1)&=&V_1 \\ T(x^2)-T(1)&=&V_2 \\ 2T(x^2)+T(x)-2T(1)&=&V_3 \end{array}\right.
\left(\begin{array}{rrr|r} 0 & 1 & 1 & V_1\\ 1 & 0 & -1& V_2 \\ 2&1&-2&V_3 \end{array}\right) \approx \left(\begin{array}{rrr|r} 1&0&-1&V_2 \\ 0&1&1&V_1 \\ 0&1&0&V_3 -2V_2 \end{array}\right)
Por consiguiente, T(ax^2+bx+c) = {\left(\begin{array}{c} b \\ 2a-b+c\\ 4a-2b+3c \end{array}\right)}
Ejemplo. Se consideran los conjuntos de vectores R y R', cuyas coordenadas se asocian a los puntos que forman los rombos ABCD y A'B'C'D' como se aprecia en la figura a continuación:Si se define T{:}\ \mathbb{R^2}\rightarrow \mathbb{R^2} como T(x,y)=(-y,2x), grafique R''=T(R'); además, verifique que T es una transformación lineal.
Solución.
\begin{array}{l} {A'=(x,y)=(4,-4)\longrightarrow T(x,y)=(-y,2x)=(4,8)=A''}\\{B'=(x,y)=(6,-4)\longrightarrow T(x,y)=(-y,2x)=(4,12)=B''}\\{C'=(x,y)=(2,-2)\longrightarrow T(x,y)=(-y,2x)=(2,4)=C''}\\{D'=(x,y)=(4,-2)\longrightarrow T(x,y)=(-y,2x)=(2,8)=D''}\end{array}Por consiguiente, el conjunto de vectores R'' tiene como coordenadas los puntos que conforman el rombo A''B''C''D'' como se aprecia en la figura a continuación:
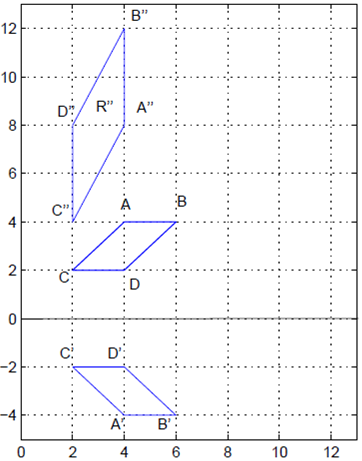
Para verificar que T es una transformación lineal, por definición se debe satisfacer las siguientes condiciones:
1) \forall\ v_1, v_2\in V{:}\ T(v_1+v_2)=T(v_1)+T(v_2).
Sean v_1=(x,y) y v_2=(x',y') dos vectores de \mathbb{R^2}.
\begin{array}{rcl} T(v_1+v_2)&=&T((x,y)+(x',y')) \\ &=&T(x+x',y+y')\\ &=&(-(y+y'),2(x+x')) \\ &=&(-y-y',2x+2x') \\ &=&(-y,2x)+(-y',2x') \\ &=&T(v_1)+T(v_2)\end{array}2) \forall\ v\in V,\ \forall \alpha\in \mathbb{R}{:}\ T(\alpha v)=\alpha T(v).
Sean v=(x,y) un vector de \mathbb{R^2} y \alpha \in \mathbb{R}.
\begin{array}{rcl} T(\alpha v)&=&T(\alpha (x,y))\\&=&T(\alpha x,\alpha y)\\&=&(-\alpha y,2\alpha x)\\&=&\alpha(-y,2x)\\&=&\alpha T(v)\end{array}Por consiguiente, T es una transformación lineal.
Enlaces de interés
Clase Online Socrative Student Plataforma SIDWeb Referencias Bibliográficas
![Álgebra lineal [MATG1003]](http://blog.espol.edu.ec/matg1003/files/2018/09/cropped-nube-matg1003.png)