Referencia: Lathi 1.8-1 p111. Oppenheim problema 2.61c p164, Ejemplo 9.24 p700
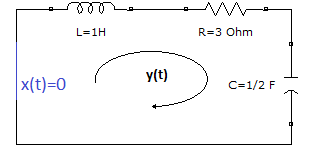Siguiendo con el ejemplo de la referencia planteado en «Sistema LTIC – Modelo entrada-salida» y las instrucciones del desarrollo analítico para «LTIC – Respuesta entrada cero«, se tiene la expresión:
Se prefiere escribir el termino de mayor orden primero y para entrada cero.Se tiene que x(t)=0, con condiciones iniciales y(0)=0, y'(0)=-5.
(D^2 + 3D +2)y(t) = 0Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python ] [Runge-Kutta d2y/dx2] [Simulador]
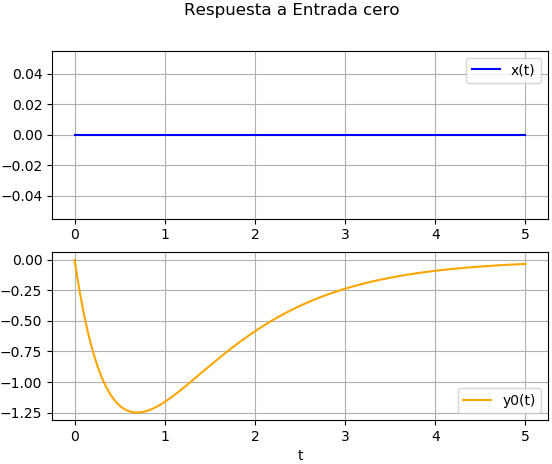
2. Respuesta entrada cero – desarrollo numérico con Scipy-Python
Esta forma de describir el problema simplifica el desarrollo a partir de la descripción de la ecuación del sistema.
Scipy define un sistema LTI usando los coeficientes de la ecuación ordenados como la expresión P(D)/Q(D con la función Scipy.signal.lti().
Se describe una señal de entrada x(t), muestreada en un intervalo [a,b] junto a las condiciones iniciales en un vector [y'(0),y(0)].
El resultado será la simulación del paso de la señal x(t) por el sistema LTI, usando la función scipy.signal.lsim(), con lo que se obtiene la respuesta del sistema y(t) y los componentes yc=[yi(t),y0(t)], donde y0(t) representa la respuesta a entrada cero.
El algoritmo tiene el siguiente resultado:
Instrucciones en Python
# Sistema lineal usando scipy.signal # Q(D)y(t)=P(D)x(t) # ejemplo: (D^2+3D+2)y(t)=(D+0)x(t) import numpy as np import scipy.signal as senal import matplotlib.pyplot as plt # INGRESO # tiempo [a,b] intervalo observación a = 0 ; b = 5 # intervalo tiempo [a,b] muestras = 41 # Señal de entrada x(t) = 0 x = lambda t: t*0 # Sistema LTI # coeficientes Q P de la ecuación diferencial Q = [1., 3., 2.] P = [1., 0.] # condiciones iniciales [y'(0),y(0)] cond_inicio = [-5,0] # PROCEDIMIENTO # intervalo observado ti = np.linspace(a, b, muestras) xi = x(ti) sistema = senal.lti(P,Q) # respuesta entrada cero [t_y, yi, yc] = senal.lsim(sistema, xi, ti, cond_inicio) # respuesta a impulso [t_h, hi] = sistema.impulse(T = ti) # SALIDA - GRAFICA plt.subplot(211) plt.suptitle('Respuesta a Entrada cero') plt.plot(ti, xi, color='blue', label='x(t)') #plt.plot(t_h, hi, color='red', label='h(t)') plt.legend() plt.grid() plt.subplot(212) # plt.plot(t_y, yi, color='magenta', label='y(t)') # plt.plot(t_y, yc[:,0], 'g-.', label='y(t)') plt.plot(t_y, yc[:,1], color='orange', label='y0(t)') plt.xlabel('t') plt.legend() plt.grid() plt.show()
Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python ] [Runge-Kutta d2y/dx2] [Simulador]
..
3. Respuesta entrada cero – desarrollo numérico con Runge-Kutta de Métodos numéricos en Python
Se reordena el sistema de ecuaciones para plantear una solución con el algoritmo Runge-Kutta de 2do orden para ecuaciones diferenciales con segundas derivadas
(D^2 + 3D +2)y(t) = 0 D^2 y(t) + 3Dy(t) + 2y(t) = 0Se ubica el término de mayor grado a la izquierda de la ecuación:
D^2 y(t) = - 3Dy(t) - 2y(t)sutituyendo las expresiones de las derivadas como las funciones f(x) por z y g(x) por z’:
Dy = y’ = z = f(x)
D2y = y" = z’= -3z – 2y = g(x)
Los valores iniciales de t0=0, y0=0, z0=-5 se usan en el algoritmo.
En este caso también se requiere conocer un intervalo de tiempo a observar [0,tn=5] y definir el tamaño de paso o resolución del resultado h=dt=0.1
El algoritmo permite obtener la gráfica y la tabla de datos.
Instrucciones en Python
# Respuesta a entrada cero # solucion para (D^2+ D + 1)y = 0 import numpy as np import matplotlib.pyplot as plt def rungekutta2_fg(f,g,x0,y0,z0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,3),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0,z0] xi = x0 yi = y0 zi = z0 for i in range(1,tamano,1): K1y = h * f(xi,yi,zi) K1z = h * g(xi,yi,zi) K2y = h * f(xi+h, yi + K1y, zi + K1z) K2z = h * g(xi+h, yi + K1y, zi + K1z) yi = yi + (K1y+K2y)/2 zi = zi + (K1z+K2z)/2 xi = xi + h estimado[i] = [xi,yi,zi] return(estimado) # PROGRAMA f = lambda t,y,z: z g = lambda t,y,z: -3*z -2*y t0 = 0 y0 = 0 z0 = -5 h = 0.1 tn = 5 muestras = int((tn-t0)/h) tabla = rungekutta2_fg(f,g,t0,y0,z0,h,muestras) ti = tabla[:,0] yi = tabla[:,1] zi = tabla[:,2] # SALIDA np.set_printoptions(precision=6) print('ti, yi, zi') print(tabla) # GRAFICA plt.plot(ti,yi, color = 'orange', label='y0(t)') plt.ylabel('y(t)') plt.xlabel('t') plt.title('Entrada cero con Runge-Kutta 2do Orden d2y/dx2 ') plt.legend() plt.grid() plt.show()
Más detalles del algoritmo de Runge-Kutta para segunda derivada en :
Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python ] [Runge-Kutta d2y/dx2] [Simulador]