Categoría: 1ra Evaluación

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

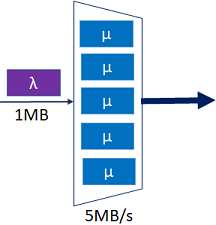
Tema 4. (35 puntos) Para transmisión de datos se dispone de un enlace con capacidad de 5 MB/s que sirve a dos clases de conexiones, tipo 1 y tipo 2, usando un multiplexor semejante al descrito en el tema anterior.

Peticiones de conexión tipo 1 llegan acorde a un proceso Poisson con tasa λ₁ y ocupan 1Mb del ancho de banda del enlace con un tiempo de uso exponencialmente distribuido con parámetro µ₁.

Peticiones conexión tipo 2 llegan acorde a un proceso Poisson con tasa λ₂ y ocupan 2Mb del ancho de banda del enlace con un tiempo de uso exponencialmente distribuido con parámetro µ₂.

Se requiere un modelo de colas para el comportamiento del sistema cuando λ₁ y λ₂ y son positivas.

a) Determine el espacio de estados del sistema

b) Dibuje y etiquete el diagrama de estados del sistema

c) Plantee las ecuaciones de estados del sistema

d) Determine la probabilidad de pérdidas de conexiones tipo 1 y tipo 2, y la probabilidad de pérdidas del sistema

e) ¿Cuál probabilidad de pérdidas es más alta? Para conexiones tipo 1 o 2, describa su respuesta

f) Calcule la utilización del enlace por cada tipo

Nota: Para los estados utilice la nomenclatura (tp1, tp2), donde tpi corresponde a la cantidad de atención de enlaces tipo i.
Para el factor de utilización, puede ponderar el ancho de banda con las probabilidades de estado asociado; es decir, cuando los servidores están ocupados, los clientes llegan juntos a una tasa de λ = λ1 + λ2 y el cliente tipo 1 se encuentra con una probabilidad de λ1/λ y de tipo 2 con una probabilidad de λ2/λ

Rúbrica: Literal a (5 puntos), literal b (10 puntos), literal c (10 puntos), literal d (5 puntos).

Referencia: Lakatos, Szeidl, Telek (2013). Introducción a sistemas de colas con telecomunicaciones. Ejercicios 11.1

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

Tema 3. (15 puntos) En telecomunicaciones, la multiplexación permite transmitir varias comunicaciones de forma simultánea combinando dos o más comunicaciones en la entrada y entregando un solo canal/ medio de salida.

Para transmisión de datos se dispone de un multiplexor con capacidad de 5 MB/s que sirve a conexiones que llegan acorde a un proceso Poisson con tasa λ y ocupan 1Mb del ancho de banda del enlace con un tiempo de uso exponencialmente distribuido con parámetro µ.

a) Determine el espacio de estados del sistema

b) Dibuje y etiquete el diagrama de estados del sistema

c) Calcule las probabilidades de cada estado (PMF)

d) Encuentre la probabilidad de pérdidas de conexiones.

e) ¿Cuál es el factor de utilización del enlace?

Rúbrica: literal a y b (5 puntos), literal c (8 puntos), literal d y e (2 puntos)

Referencia: Erlang’s loss System. Ross 8.9.1. p.563, M/M/c/c Queueing System. León-García 12.4.3

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

Tema 2. (35 puntos) Para comunicar dos ciudades se instalan tres radio-enlaces digitales de larga distancia, cada uno conformado por un transmisor (Tx) y un receptor (Rx). Por ejemplo, las ciudades Guayaquil en la costa y Cuenca en la sierra, se comunican usando tres radio-enlaces que en puntos por tramos en las montañas.

En un radio-enlace el dígito binario 0 enviado por Tx se recibe en Rx con una probabilidad de error α, mientras que el dígito binario 1 presenta probabilidad de error β.

Para un radio-enlace realice un modelo con una Cadena de Markov:

a) Determine el espacio de estados

b) Realice el diagrama de estados, etiquete claramente

c) Escriba la matriz de transición y calcule la probabilidad de estado estable.

Suponga que α=0.01, β=0.02 y determine para todo el enlace entre las ciudades:

d) La matriz de transición entre las ciudades A y B
e) Probabilidad de error para un dígito binario 0 (bit)
f) Probabilidad de error para un bit con valor 1 (bit)
g) El error al transmitir un bit en todo el enlace
h) Observe y comente sus resultados.

Rúbrica: literal a y b (6 puntos), literal c (4 puntos), literal d (10 puntos), literal e y f (3 puntos c/u) literal g (4 puntos), literal h (5 puntos)

Referencia: Gubner(2006) problema 1.56, 3.28, ejemplo 3.13; León-García(2008) 1.5.1; FIEC03236-1ra Evaluación II Término 2011.

1ra Evaluación II Término 2017-2018. Noviembre 28, 2017

Tema 1. (15 puntos) El código Morse fué muy usado en telegrafía, transmisiones por radio marítimas y aéreas. Conocido también como alfabeto Morse, cambia los caracteres alfanuméricos a códigos combinando puntos '.' y rayas '-'.
La separación entre códigos morse se realiza con un espacio ' ', mientras que en la separación entre palabras se usan 3 espacios '   '.

Ejemplo:
un mensaje: ESPOL impulsando la sociedad del conocimiento
. ... .--. --- .-..   .. -- .--. ..- .-.. ... .- -. -.. ---   .-.. .-   ... --- -.-. .. . -.. .- -..   -.. . .-..   -.-. --- -. --- -.-. .. -- .. . -. - --- 

Realice un modelo en cadena de Markov para un experimento realizado sobre un texto codificado en morse.

Use como referencia los símbolos = '.- ', en el experimento se contaron los cambios entre símbolos mostrado los valores resultantes en la matriz “conteo”.

a) Determine el espacio de estados
b) Realice el diagrama de estados
c) Escriba la matriz de transición y ubique los valores encontrados en el diagrama.
d) Calcule la probabilidad de estado estable o largo plazo.

conteo = 
[[36532, 35233, 51578],
 [36982, 23931, 30807],
 [49822, 32564, 32194]]

Referencia: http://blog.espol.edu.ec/estg1003/morse-codificador-texto/
Rúbrica: literal a y b (5 puntos), literal c (5 puntos), literal d (5 puntos)

1ra Evaluación I Término 2017-2018. Junio 27, 2017

Call Center Operadora y Dos Técnicos

Tema 3 (30 puntos). Para obtener soporte técnico de un proveedor de internet se llama al número telefónico del call-center donde se encuentra una recepcionista y dos técnicos. Los clientes llaman a intervalos de tiempo de 10 minutos, distribuidos exponencialmente.

En una llamada, los clientes son atendidos por la recepcionista que toma los datos y redirige la llamada a uno de los técnicos disponibles. Si un cliente llama mientras la recepcionista atiende otra, el cliente recibe tono de ocupado y la pierde.

La recepcionista al pasar una llamada a los técnicos puede suceder que:

• Si ambos están disponibles, se selecciona uno con igual probabilidad.
• Si solo hay uno disponible, se le asigna la llamada.
• Si los dos técnicos están ocupados, se pierde la llamada.

Considere a un cliente como “satisfecho” si su llamada fue procesada por la recepcionista y cualquiera de los técnicos.
Los tiempos de atención siguen distribuciones exponenciales: recepcionista es de 3 minutos y por técnico es de 15 minutos.

a) ¿Cuáles son los estados para un modelo Markov?
b) Dibuje un modelo de Markov para el problema.
c) Etiquete cada una de las conexiones.
d) En estado estable, ¿cuáles son las probabilidades de encontrarse en cada estado?
e) Encuentre la probabilidad que los técnicos estén ocupados.
f) ¿Cuál es la probabilidad que una llamada se pierda en la recepción?
g) ¿Cuál es la tasa de clientes satisfechos? (salida del sistema, throughput)

Referencias: Chun Tung Chou. COMP9334 Capacity Planning of Computer Systems and Networks.

Rúbrica: literal a y b (10 puntos), literal c (5 puntos), literal d (5 puntos), literal e (4 puntos), literal f y g (6 puntos).