2da Evaluación III Término 2012-2013. Marzo 20, 2013. FIEC03236
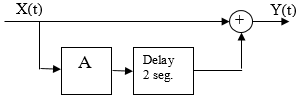
Tema 3 (40 puntos). Dada la figura, asuma que el proceso es estocástico:
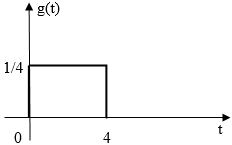
Siendo X(t) = A*g(t), donde A es una variable aleatoria que toma los valores -1 y +1 con igual probabilidad, determine:
a) La función (pmf) probabilidad de masa de X(t)
b) E[X(t)], Var[X(t)]
c) La pmf conjunta de X(t) y X(t+d)
d) La CX(t, t+d), d>0
Rúbrica: cada literal (10 puntos)