Categoría: Evaluaciones

1ra Evaluación III Término 2012-2013. Marzo 20, 2013. FIEC03236

Tema 3 (40 puntos). Sea (X,Y) una variable aleatoria bidimensional con función de densidad de probabilidad dada por:

f_{XY}(x,y) = \begin{cases} Kx && , 0 \leq y \leq 2x <2 \\ 0 && ,\text{otro caso} \end{cases}

a) Graficar la región de f_XY(x,y)

Determinar:

b) el valor de K para que sea una función densidad de probabilidad

c) P(Y>X│Y<1)

d) P(√X│Y=1,5)

e) E[XY]

f) Var[X]

g) F_Y(y)

Rúbrica: literal a (3 puntos), b,c,e,f (5 puntos), d (10 puntos), g (7 puntos)

1ra Evaluación II Término 2012-2013. Noviembre 29, 2012. FIEC03236

Tema 3 (40 puntos). Sean las variables aleatorias X y Y con función de densidad conjunta :

f_{XY}(x,y) = k*y(1-x-y)

Si (x,y) pertenece al recinto limitado por las rectas x + y = 1; x = 0; y = 0.

a) Calcular el valor de k
b) Calcular la función de distribución de la variable aleatoria bidimensional F(x,y)
c) Calcular las funciones de densidad marginales

Nota: literal a y c (10 puntos), literal b (20 puntos)

1ra Evaluación II Término 2012-2013. Noviembre 29, 2012. FIEC03236

Tema 2 (40 puntos). La variable aleatoria X tiene por función de densidad f_X(x), y se define la variable aleatoria Y=g(x).

F_{X}(x) = 2 * \begin{cases} 0.5x + 0.5 && , x \in (-1,0] \\ -0.5x + 0.5 && , x \in (0,1] \\ 0 && , x \in (-\infty , 1] \cup (1, \infty) \end{cases}

a) Determinar b para que P(|X|<b) = 1/5

b) Si g(x)=x², encuentre y grafique:

b.1 La función de distribución de probabilidad de Y

b.2 La función de densidad de probabilidad de Y

Nota: literal a (10 puntos), literal b.1 y b.2 (15 puntos) cada uno

1ra Evaluación II Término 2012-2013. Noviembre 29, 2012. FIEC03236

Tema 1 (20 puntos). Una fuente binaria emite de manera equiprobable e independientemente un bloque de tres dígitos (0 o 1) cada segundo.

De cada bloque se envía a  un canal de transmisión un cero si en el bloque hay más ceros que unos y un uno en caso contrario.

El canal transmite el digito con una probabilidad de error p, y el receptor reconstruye la terna, repitiendo tres veces el digito que se ha recibido.

Determine:

a) ¿Cuál es el número de bits erróneos por bloque? (10 puntos).

b) ¿Cuál debería ser la probabilidad p, para que este valor medio no fuese mayor que 1? (10 puntos).

3ra Evaluación II Término 2012-2013. Febrero 14, 2013. FIEC03236

Tema 4 (20 puntos) Dada la siguiente función de Autocorrelación R_X(ζ) del proceso estocástico X(t) que es WSS.

a) Encuentre Var[X(t)].

b) Determine y grafique S_x(ω) ó S_x(f).

Rúbrica: 10 puntos cada literal

3ra Evaluación II Término 2012-2013. Febrero 14, 2013. FIEC03236

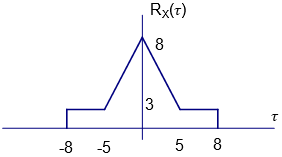
Tema 3 (25 puntos). Sea X(t) un proceso estocástico normal y estacionario, con autocorrelación:

R_{X} = \frac{1}{1+\tau ^2} +1

Determinar:

a) P(|X(2)| ≤ 2)

b) La matriz de covarianzas de la variable aleatoria tridimensional [X(0), X(1), X(3)]

c) La función de densidad de la variable aleatoria Z=X²(2)

d) La autocorrelación del proceso estocástico Y(t)=4*X(t+1)+t

Rúbrica:  literal a (4 puntos), literal b (6 puntos), literal c (10 puntos), literal d (5 puntos)