Cuando se habla de linealidad en matemáticas, ésta se refiere a un conjunto de propiedades que se generalizan de aquellas relacionadas con el concepto de línea recta. En \mathbb{R}^{2} una ecuación lineal corresponde a una línea recta. Por ejemplo, la expresión 2x+3y=6 tiene una gráfica correspondiente a una línea recta en el plano cartesiano:
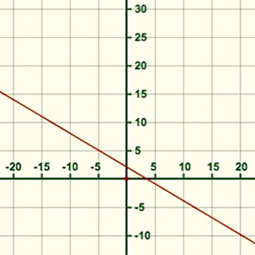
En dimensiones superiores graficar no es siempre posible, sin embargo las propiedades se pueden estudiar de todos modos. En \mathbb{R}^{3}, por ejemplo, la ecuación lineal 2x-2y+3z=5 corresponde a un plano:
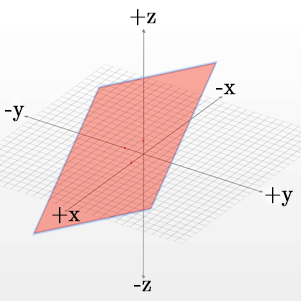
Una ecuación puede considerarse como un predicado de varias variables; en los ejemplos anteriores se tiene que: p(x,y):2x+3y=6, donde \mathbb{R}^{2} es el referencial; y p(x,y,z):2x-2y+3z=5, donde \mathbb{R}^{3} es el referencial. Así, el conjunto solución de tales predicados corresponde al conjunto de puntos graficados respectivamente. Por otra parte, un Sistema de Ecuaciones Lineales (S.E.L.) es una conjunción de predicados (ecuaciones lineales) de modo que la solución del sistema es la intersección de los conjuntos solución de cada una de las ecuaciones.
Definición. Una ecuación lineal es una ecuación algebraica cuyos términos son constantes o el producto de una constante por una variable a la primera potencia. Puede contener variables diferentes en términos diferentes, pero el producto entre variables no es admitido. Ejemplos de ecuaciones lineales son 3x-5y-7=0 o z=-4y+2.
Definición. Un Sistema de Ecuaciones Lineales (S.E.L.) es una colección de m ecuaciones lineales que involucran el mismo conjunto de variables. Los conjuntos solución de cada ecuación del sistema están en un mismo referencial (por ejemplo, \mathbb{R}^{2}, \mathbb{R}^{3}, \mathbb{R}^{4}, etc), y la solución del sistema corresponde a la intersección todos los conjuntos solución.
Ejemplo. Un sistema de 2 ecuaciones lineales en \mathbb{R}^{3} tiene 3 incógnitas. \left\{ \begin{array}{rcl}x+y-z&=&2 \\ 2x-2y+z&=&4 \end{array}\right.
Ejemplo. Un sistema de 3 ecuaciones lineales en \mathbb{R}^{2} tiene 2 incógnitas. \left\{ \begin{array}{rcl}2x-3y&=&6 \\ x-3y&=&0 \\ 3x-3y&=&12 \end{array}\right.
El símbolo «\left\{ \right.» indica que las ecuaciones están conectadas mediante conjunción; por lo tanto, resolver un S.E.L. implica encontrar el conjunto solución que corresponde a la intersección de los conjuntos solución de cada ecuación. Se ilustra gráficamente en la siguiente figura: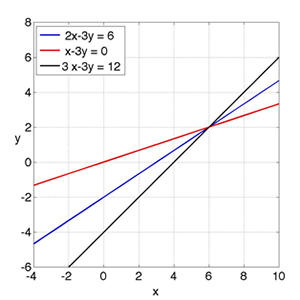
Resolver gráficamente el S.E.L. no es procedente, así que varios métodos existen para esto. El método recomendado en este curso utiliza la representación con matriz aumentada, porque facilita hallar la información contenida en el sistema; y las operaciones de renglón para reducir el sistema a uno equivalente.
La representación con matriz aumentada de \left\{ \begin{array}{rcl}2x-3y&=&6 \\ x-3y&=&0 \\ 3x-3y&=&12 \end{array}\right.es \left(\begin{array}{cc|c}2 & -3 & 6 \\ 1 & -3 & 0 \\ 3 & -3 & 12 \end{array}\right)
y su resolución mediante operaciones de renglón es:
\left(\begin{array}{rr|r} 2 & -3 & 6\\ 1 & -3 & 0\\ 3 & -3 & 12 \end{array}\right) \begin{array}{c} \stackrel{f_{1} {\leftrightarrow} f_{2}}{\longrightarrow} \end{array}\left(\begin{array}{rr|r}1 & -3 & 0\\2 & -3 & 6\\3 & -3 & 12\end{array}\right) \begin{array}{c} {\scriptsize f_{2}-2f_{1}} \\ \longrightarrow \\ {\scriptsize f_{3}-3f_{1}}\end{array} \left(\begin{array}{rr|r} 1 & -3 & 0\\0 & 3 & 6\\0 & 6 & 12\end{array}\right) \stackrel{f_{3}-2f_{2}}{\longrightarrow}\left(\begin{array}{rr|r}1 & -3 & 0\\0 & 3 & 6\\0 & 0 & 0\end{array}\right) \stackrel{f_{1}-f_{2}}{\longrightarrow} \left(\begin{array}{rr|r}1 & 0 & 6\\0 & 3 & 6\\0 & 0 & 0\end{array}\right)
Por operaciones de renglón se reduce el sistema original y se lo representa con un sistema equivalente en el cual encontrar los valores de las incógnitas presentes es más práctico.
\left\{\begin{array}{rcl}x&=&6\\3y&=&6\end{array}\right.La solución del S.E.L. es (x,y)=(6,2). Nótese como una ecuación trivial de la forma 0x+0y=0 no produce información significativa, pues su conjunto solución es todo el referencial, Re=\mathbb{R}^{2}.
¿Qué sucede al aplicar las operaciones de renglón en un S.E.L.?
Se modifica el sistema de ecuaciones, simplificando (reduciendo) su estructura, pero no se modifica el conjunto solución. En el proceso se elimina información redundante, representada por la ecuación que genera una fila de ceros, hasta obtener solo dos ecuaciones cuyo conjunto solución es idéntico al conjunto solución del S.E.L. original. Gráficamente se tiene: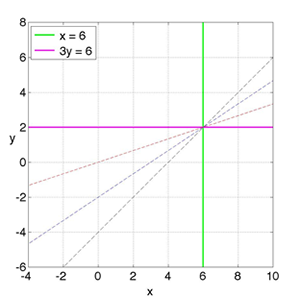
Naturalmente los procesos que se presentan no pueden siempre graficarse y en la mayoría de ocasiones se resuelven analíticamente sin recurrir a gráficos; pero es muy importante recalcar que la solución del S.E.L. la conforman la intersección de los conjuntos soluciones de todas las ecuaciones que componen el sistema.
Inconsistencia e infinitas soluciones
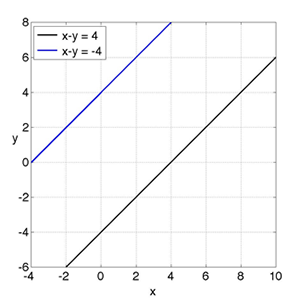
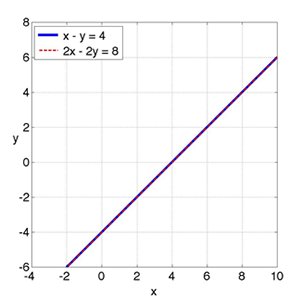
Un S.E.L. se denomina inconsistente cuando no tiene solución (la intersección es vacía) o se dice que tiene infinitas soluciones cuando la intersección de los conjuntos solución contiene infinitos puntos; son ejemplos de estos casos los siguientes S.E.L.:
El S.E.L. del literal a) representa dos líneas paralelas que nunca se intersectan (conjunto solución vacío) y el S.E.L. del literal b) representa dos líneas rectas coincidentes en todos sus puntos (infinitas soluciones); gráficamente se tiene:
¿Cómo se identifica numéricamente un S.E.L. inconsistente?
Cuando un S.E.L. constituye un sistema inconsistente, una de las ecuaciones presenta un conjunto de solución vacío. Aplicando la representación con matriz aumentada en el S.E.L. del literal a) y desarrollando las operaciones de renglón correspondientes para reducir el sistema a uno equivalente se tiene:
\left(\begin{array}{rr|r} 1 & -1 & 4\\ 1 & -1 & -4 \end{array}\right) \stackrel{f_{2}-f_{1}}{\longrightarrow} \left(\begin{array}{rr|r} 1 & -1 & 4\\ 0 & 0 & -8 \end{array}\right) Se puede observar que la segunda ecuación se simplificó como 0x+0y={-8}; por lo tanto, es imposible que el S.E.L. tenga solución. Nótese que al reemplazar cualquier número en x e y, cada uno éstos se multiplican por cero y al sumarlos nunca se obtendrá el resultado de {-8}.
Por consiguiente, el conjunto solución de la ecuación es vacío (\textrm{Ø}) y no importa cuál es el conjunto solución de la otra ecuación porque al intersectarse con el conjunto vacío genera como resultado el conjunto vacío.
¿Cómo se identifica numéricamente un S.E.L. con infinitas soluciones?
Cuando un S.E.L. constituye un sistema con infinitas soluciones, el conjunto solución no presenta valores numéricos exactos sino que depende de una o más variables libres (o parámetros). Aplicando la representación con matriz aumentada en el S.E.L. del literal a) y desarrollando las operaciones de renglón correspondientes para reducir el sistema a uno equivalente se tiene:
\left(\begin{array}{rr|r} 1 & -1 & 4\\ 1 & -1 & 4 \end{array}\right) \stackrel{f_{2}-f_{1}}{\longrightarrow} \left(\begin{array}{rr|r} 1 & -1 & 4\\ 0 & 0 & 0 \end{array}\right) Se puede observar que la segunda ecuación se vuelve trivial y no aporta información debido a que el conjunto solución es el referencial, Re=\mathbb{R}^{2}. Nótese que el conjunto solución del S.E.L. depende de la primera ecuación, x-y=4. A partir de esta ecuación es imposible obtener una solución numérica específica sino que una de las variables depende de la otra.
Si se elige expresar la variable x en términos de la variable y, la solución es la ecuación x=y+4, donde y\in R; es decir, x es la variable dependiente mientras que y es la variable libre. Por otra parte, si se elige expresar la variable y en términos de la variable x, la solución es la ecuación y=x-4, donde x\in R; es decir, x es la variable libre mientras que y es la variable dependiente. En cualquier situación, existe al menos una variable libre, lo que determina que el S.E.L. tenga infinitas soluciones.
Nota: El hecho que un S.E.L. tenga una o más filas de ceros en su representación con matriz aumentada, NO implica que el S.E.L. tenga infinitas soluciones; sino que la solución, de existir, NO dependerá de tales filas de ceros (pues corresponden a ecuaciones triviales cuya solución es todo el referencial), sino que dependerá de las ecuaciones no triviales restantes.
Como un ejemplo, se presenta el siguiente S.E.L.:
\left\{ \begin{array}{rcl}2x-3y&=&6 \\ x-3y&=&0 \\ 3x-3y&=&12 \end{array}\right.el cual tiene solución única independientemente de que, al resolverlo, aparezca una fila de ceros en su representación con matriz aumentada.
Un sistema tiene infinitas soluciones siempre y cuando sea consistente y presente variables libres.
Enlaces de interés
Clase Online Plataforma SIDWeb Referencias Bibliográficas
