Sean B_1=\{ p(x),q(x),r(x) \} y B_2=\{s(x),t(x),u(x)\} dos bases ordenadas de \mathbb{P}_2. Si se conoce que:\begin{aligned}[x^2-x]_{B_1} &= (1,1,0)\\ {[x+1]_{B_1}}&=(0,1,0) \\ {[2x^2+1]_{B_1}}&=(1,-1,1) \\ {[s(x)+t(x)]_{B_1}}&=(1,1,0) \\{[t(x)+u(x)]_{B_1}}&=(5,2,0) \\{[u(x)]_{B_1}}&=(3,0,0) \end{aligned}Determine los vectores de cada base.
Categoría: Término 2
Tema 4
En el espacio vectorial de \mathbb{P}_3 se definen los siguientes subespacios vectoriales\begin{aligned} H&=gen\{ 2x^3+x^2,x+1 \} \\ W&=gen\{ 2-x,3+3x \} \end{aligned}Determine H\cap W y H+W junto con sus respectivas bases y dimensiones.
Tema 3
Sea V el espacio vectorial de \mathbb{P}_2 con producto interno\langle p,q \rangle=p(-1)q(-1)+p(0)q(0)+p(1)q(1)Considere el subespacio vectorial de V definido comoW=\{ p(x)\in\mathbb{P}_2\; ; \; p'(-1)=p'(1) \}Escriba el vector p(x)=x^2+2x como la suma de dos vectores de V, uno de W y otro de W^{\perp}.
Tema 2
Sea T una transformación lineal definida como T:\mathbb{R}^2\longrightarrow\mathbb{R}^3 con reglas de correspondenciaT\begin{pmatrix} a\\b \end{pmatrix}=\begin{pmatrix} \begin{aligned} a&+2b\\a&+b\\a&-b \end{aligned} \end{pmatrix}
a. Encuentre una base y dimensión del núcleo y recorrido de T.
b. Halle la matriz asociada a T con respecto a las bases B=\{ (1,-1),(2,1) \} de \mathbb{R}^2 y B'=\{ (1,1,0),(1,0,1),(0,1,1) \} de \mathbb{R}^3.
Tema 1
Una empresa produce tres productos, los mismos que se procesan en tres máquinas. El tiempo en horas requerido para procesar una unidad de cada producto por las tres máquinas se da a continuación:
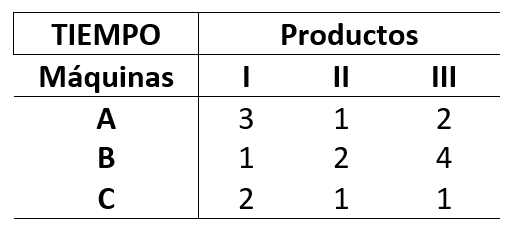
Se dispone de la máquina A por 850 horas, de la máquina B por 1200 horas y de la máquina C por 550 horas. ¿Cuántas unidades de cada producto deberían producirse con objeto de emplear todo el tiempo disponible de las máquinas?
Tema 5
Sea el espacio vectorial V=P_2. Se define el siguiente producto interno\langle p,q \rangle=p(0)q(0)+p(1)q(1)+p(-1)q(-1)y además, el operador lineal T sobre V comoT(p(x))=p(-1)+p(0)x^2Hallar la proyección ortogonal del vector r(x)=x^2-x-1 sobre el complemento ortogonal del núcleo de T.
Tema 4
Sea la matriz A=\begin{pmatrix} \begin{array}{rr} -4&6\\-3&5 \end{array} \end{pmatrix}. Determine la matriz A^k, siendo k\in\mathbb{N}.
Tema 3
Sea V=C[0,1] el espacio vectorial de las funciones continuas en el intervalo [0,1] con producto interno\langle f,g \rangle=\int_{1}^{0} f(x) g(x) dxEncuentre un polinomio de grado menor o igual a 1 que mejor aproxime a la funciónf(x)=e^{-x} con x\in [0,1].
Nota: Suponga a los polinomios de grado menor o igual a 1 como un subespacio vectorial de V.
Tema 2
Sea T:\mathbb{R}^4\longrightarrow\mathbb{R}^4 una transformación lineal definida comoT(x,y,z,w)=(0,x,x+y,x+y+z)Se conoce también que v=(1,0,0,0).
Pruebe que B=\{v,T(v),T^2(v),T^3(v)\} es un conjunto linealmente independiente en \mathbb{R}^4.
Tema 1
Califique las siguientes proposiciones como verdaderas o falsas, justifique su respuesta. Puede escribir un contraejemplo si considera que la proposición es falsa.
a. Si A es una matriz de tamaño n\times n, u y v son vectores de \mathbb{R}^n, entonces se cumple que \langle Av,u \rangle=\langle v,A^T u \rangle.
Nota: \langle u,v \rangle representa el producto interno.
b. Sea V un espacio vectorial y T un operador lineal definido sobre V, entonces se cumple que Nu(T^2) \subseteq Nu(T).
c. Sea A y B matrices semejantes, entonces las matrices A^T y B^T también lo son.
d. Sea T:V\longrightarrow W una transformación lineal. Si \{v_1,v_2,...,v_n\} es un conjunto linealmente independiente en V, entonces el conjunto \{T(v_1),T(v_2),...,T(v_n)\} es linealmente independiente en W.
