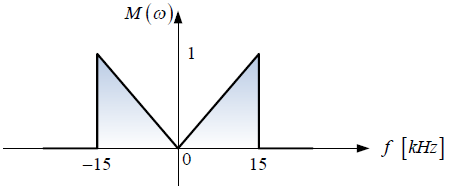Categoría: Evaluaciones

3ra Evaluación I Término 2014-2015. 18/Septiembre/2014. TELG1001

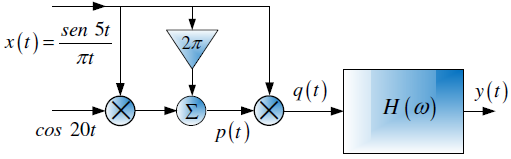
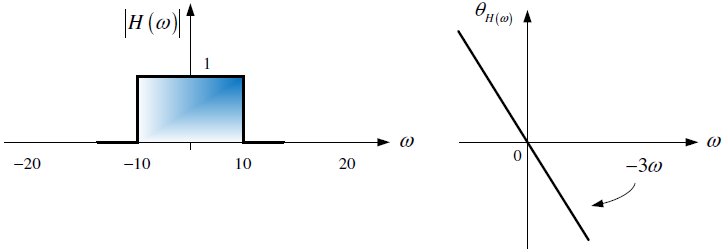
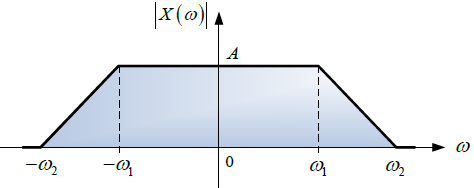
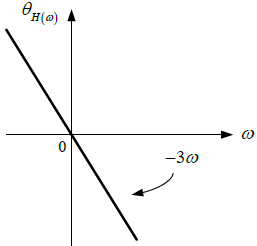
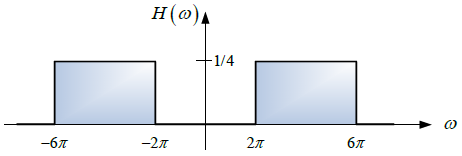
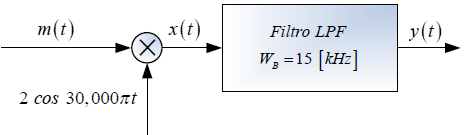
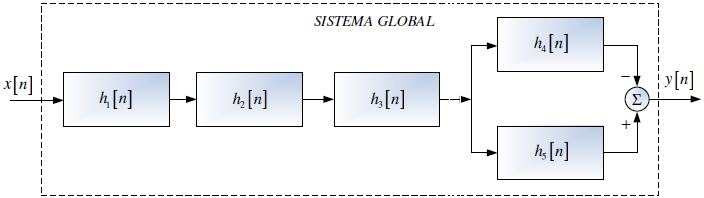
Tema 2. (35 puntos) Considerar la existencia del sistema mostrado en la siguiente figura, donde el espectro de Fourier de su respuesa impulso h(t) es H(ω) vs ω.

Determinar, esquematizar y etiquetar, según corresponda lo siguiente:

a. El espectro de Fourier de p(t), es decir P(ω) vs ω.

b. La expresión analítica de q(t), como una función de x(t).

c. El espectro de Fourier de q(t), es decir Q(ω) vs ω.

d. El espectro de Fourier de y(t), es decir Y(ω) vs ω.

e. La salida o respuesta de dicho sistema. es decir y(t) sin esquematizar, ni etiquetar.

---

Coordinador: Tama Alberto

3ra Evaluación II Término 2012-2013. 14/Febrero/2013. TELG1001

Tema 1. (40 puntos) Una señal de entrada x(t) es muestreada mediante la utilización de un tren de impulsos s(t). Su resultante z(t) es utilizada como la excitación de un sistema LTI-CT, cuya respuesta de frecuencia H(ω) está representada en la siguiente figura:

a. Condediendo el hecho que

s(t) = \sum_{k=-\infty}^{\infty} \delta (t-k/2)

determinar, esquematizar y etiquetar su representación mediante series de Fourier armónicas, es decir C_k vs k.

b. Determinar, esquematizar y etiquetar la transformada de Fourier de la señal z(t), es decir Z(ω).

c. Utilizando la inversa de la transformada de Fourier, determinar la respuesta impulso del precitado sistema LTI-CT, es decir h(t).

d. Obtener el valor de la energía de las señales x(t) y h(t), es decir E_x(t) y E_h(t).

e. Determinar, esquematizar y etiquetr la transformada de Fourier de la señal y(t), es decir Y(ω)-

f. Obtener la respuesta y(t) y la energía asociada E_y(t) del precitado sistema LTI-CT.

---

Coordinador: Tama Alberto

3ra Evaluación I Término 2012-2013. 13/Septiembre/2012. TELG1001

Tema 4. (25 puntos) El sistema mostrado en la siguiente figura, es utilizado para distorsionar las señales de audio (scrambler-scrambling).

La señal x(t) es la versión modulada de la señal de entrada m(t), la misma que es la entrada a un filtro ideal pasa bajo, cuyo ancho de banda es de 15 [kHz]. De igual manera, también se puede afirmar que la salida del filtro pasa bajo y(t) es la versión distrorsionada de la señal de entrada m(t).

a. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal x(t); es decir X(ω) vs ω.

b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal y(t); es decir Y(ω) vs ω.

c. Utilizando la inversa de la Transformada de Fourier, determinar, esquematizar y etiquetar la señal de salida y(t).

---

Coordinador: Tama Alberto