Categoría: Video_Tutorial y otros

Referencia: Leon-Couch, 3–8 Modulación Delta, p.192 ; Delta-sigma_modulation Wikipedia

La modulación Sigma-Delta (∑Δ ) codifica una señal analógica a digital generando una secuencia de +1 y -1 (impulsos) que representan la diferencia entre la señal analógica muestreada y la señal digital acumulada. Tiene aplicaciones en sintetizadores de frecuencia, fuentes de poder conmutadas y controladores de motor.

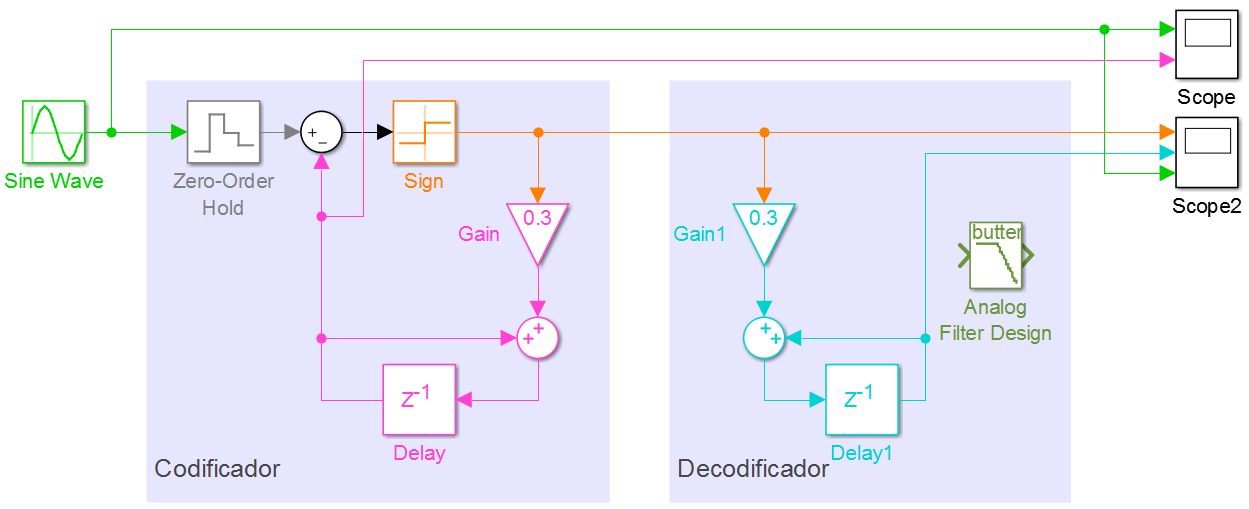
El sistema en diagrama de bloques en simulink se muestra en la figura:

La señal de entrada (Sine Wave) se cuantifica en (Zero-Order Hold).

Luego se obtiene el signo (sign) de la diferencia entre la señal de entrada y la señal digital acumulada (∑) que genera la secuencia de +1 y -1 en la salida del codificador.

El valor de la ganancia Δ=0.3 representa el valor del escalón de subida o bajada de la señal digital acumulada, representada en color magenta.

La secuencia de salida +1 y -1, de nuevo acumulada en el decodificador, permite obtener una versión digital cercana a la señal analógica inicial.

---

CODIFICADOR Sigma-Delta

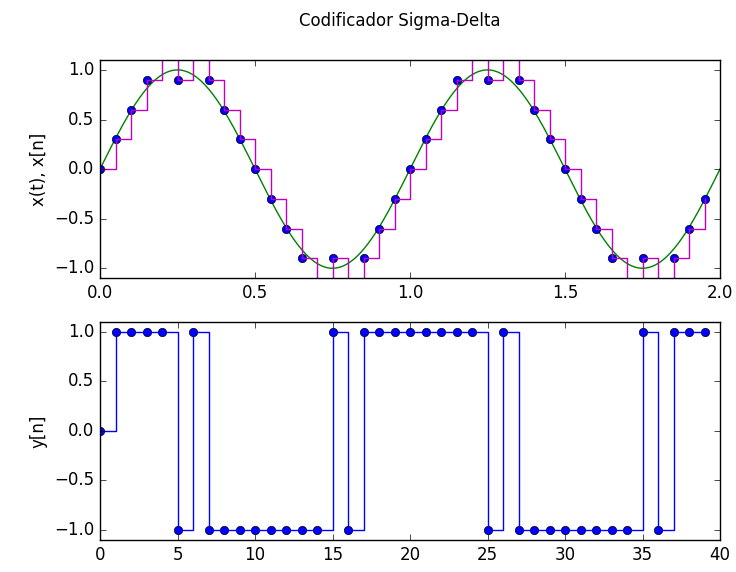
La señal de entrada para el ejemplo tiene frecuencia fs=1 Hz, Δ=deltaY=0.3, rango [0,tn] hasta 2 segundos con divisiones k=40 en el rango de tiempo.

>>> 
rango [0,tn]:2
Secciones en el rango k:40
[ 0  1  1  1  1 -1  1 -1 -1 -1 -1 -1 -1 -1 -1
  1 -1  1  1  1  1  1  1  1  1 -1  1 -1 -1 -1
 -1 -1 -1 -1 -1  1 -1  1  1  1]
[  0.05   0.3   40.  ]

El script genera la gráfica y los archivos para datos y parámetros en formato texto.

La señal de entrada y los valores pueden ser modificados en el script adjunto:

# Modulacion Delta - Codificador
# entrada x(t), salida: y[n]
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt

# Definir la funcion de Entrada
def entradax(t,fs):
    x = np.sin(2*np.pi*fs*t)
    return(x)

# PROGRAMA para la modulación
# INGRESO
t0 = 0
tn = float(input('rango [0,tn]:'))
k  = int(input('Secciones en el rango k:'))

# PROCEDIMIENTO
# Analógica Referencia
fs = 1
m  = 500  # puntos en eje t para gráfico analógica
dm = (tn-t0)/m
t  = np.arange(0,tn,dm)  # eje tiempo analógica

xanalog = np.zeros(m, dtype=float)
for i in range(0,m):
    xanalog[i] = entradax(t[i],fs)

# Codificar Sigma-Delta
deltaY = 0.3          # Tamaño delta en eje Y
deltaT = (tn-t0)/k    # Tamaño delta en eje tiempo
td     = np.arange(0,tn,deltaT)    # tiempo muestreo
muestra  = np.zeros(k, dtype=float) # analógica para comparar
xdigital = np.zeros(k, dtype=float) # digital
ysalida  = np.zeros(k, dtype=int)   # Salida de +1|-1

td[0] = t0
muestra[0] = entradax(td[0],fs)
ysalida[0] = 0
for i in range(1,k):
    muestra[i] = entradax(td[i],fs) # referencia analógica
    diferencia = muestra[i]-xdigital[i-1]
    if (diferencia>0):
        bit = 1
    else:
        bit = -1
    xdigital[i] = xdigital[i-1]+bit*deltaY
    ysalida[i]  = bit
parametros = np.array([deltaT,deltaY,k])

# SALIDA
print(ysalida)
print(parametros)
np.savetxt('sigmadelta_datos.txt',ysalida,fmt='%i')
np.savetxt('sigmadelta_parametros.txt',parametros)

# Graficar
plt.figure(1)       # define la grafica
plt.suptitle('Codificador Sigma-Delta')

plt.subplot(211)    # grafica de 2x1 y subgrafica 1
plt.ylabel('x(t), x[n]')
xmax=np.max(xanalog)+0.1*np.max(xanalog) # rango en el eje y
xmin=np.min(xanalog)-0.1*np.max(xanalog)
plt.axis((t0,tn,xmin,xmax)) # Ajusta ejes
plt.plot(t,xanalog, 'g')
plt.axis((t0,tn,xmin,xmax))
plt.plot(td,xdigital,'bo')  # Puntos x[n]
plt.step(td,xdigital, where='post',color='m')

plt.subplot(212)    # grafica de 2x1 y subgrafica 2
plt.ylabel('y[n]')
plt.axis((0,k,-1.1,1.1))
plt.plot(ysalida, 'bo')     # Puntos y[n]
puntos = np.arange(0,k,1)     #posicion eje x para escalon
plt.step(puntos,ysalida, where='post')

plt.show()

---

Decodificador Sigma-Delta

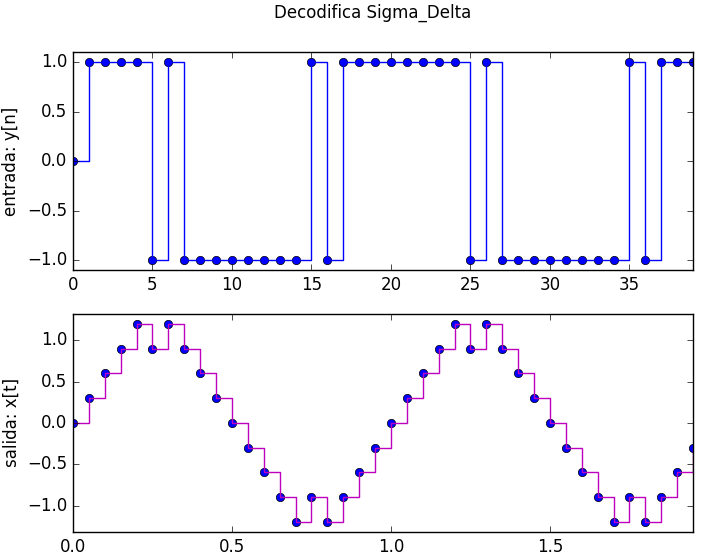
Para observar el resultado, se decodifican los datos y se obtiene el siguiente resultado:

>>>
entrada: [ 0  1  1  1  1 -1  1 -1 -1 -1 -1 -1 -1 -1 -1
           1 -1  1  1  1  1  1  1  1  1 -1  1 -1 -1 -1
          -1 -1 -1 -1 -1  1 -1  1  1  1]
salida: 
[ 0.0000000e+00   3.0000000e-01   6.0000000e-01   9.0000000e-01
  1.2000000e+00   9.0000000e-01   1.2000000e+00   9.0000000e-01
  6.0000000e-01   3.0000000e-01  -1.1102230e-16  -3.0000000e-01
 -6.0000000e-01  -9.0000000e-01  -1.2000000e+00  -9.0000000e-01
 -1.2000000e+00  -9.0000000e-01  -6.0000000e-01  -3.0000000e-01
 -1.1102230e-16   3.0000000e-01   6.0000000e-01   9.0000000e-01
  1.2000000e+00   9.0000000e-01   1.2000000e+00   9.0000000e-01
  6.0000000e-01   3.0000000e-01  -1.1102230e-16  -3.0000000e-01
 -6.0000000e-01  -9.0000000e-01  -1.2000000e+00  -9.0000000e-01
 -1.2000000e+00  -9.0000000e-01  -6.0000000e-01  -3.0000000e-01]

realizado usando el siguiente script de python:

# Modulacion Sigma-Delta Decodificador
#  entrada y[n], salida: x[n]
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
archivodatos = 'sigmadelta_datos.txt'
archivoparam = 'sigmadelta_parametros.txt'

# PROCEDIMIENTO
# Lectura de datos desde archivos
yentrada = np.loadtxt(archivodatos,dtype=int)
datos    = np.loadtxt(archivoparam,dtype=float)

deltaT = datos[0] # Tamaño delta en eje tiempo
deltaY = datos[1] # Tamaño delta en eje Y

# número de muestras
k = len(yentrada) 
xdigital = np.zeros(k, dtype=float)
punto    = np.zeros(k, dtype=int)   # número de muestra
td       = np.zeros(k, dtype=float) # tiempo muestreo

# DECOdifica Sigma-Delta
xdigital[0] = yentrada[0]
punto[0] = 0
td[0]    = 0
for i in range(1,k):
    punto[i] = i
    td[i]    = deltaT*i
    xdigital[i] = xdigital[i-1]+yentrada[i]*deltaY

# SALIDA
print('entrada:', yentrada)
print('salida:',xdigital,)

# Graficar
plt.figure(1)       # define la grafica
plt.suptitle('Decodifica Sigma_Delta')

plt.subplot(211)    # grafica de 2x1 y subgrafica 1
plt.ylabel('entrada: y[n]')
plt.axis((0,k-1,-1.1,1.1)) # Ajusta ejes
plt.plot(punto,yentrada,'bo') # Puntos y[n]
plt.step(punto,yentrada, where='post')

plt.subplot(212)    # grafica de 2x1 y subgrafica 2
plt.ylabel('salida: x[t]')
# rango en el eje y
xmax = np.max(xdigital)+0.1*np.max(xdigital)
xmin = np.min(xdigital)-0.1*np.max(xdigital)
plt.axis((0,td[k-1],xmin,xmax)) # Ajusta ejes
plt.plot(td,xdigital,'bo')
plt.step(td,xdigital, where='post', color='m')

plt.show()

---

Tarea

Realice observaciones cambiando:

a) la frecuencia de la señal de entrada,
b) el valor para deltaY
c) el rango tnd) el número de secciones en el tiempo
e) la forma de la señal de entrada a triangular, diente de sierra, exponencial periódica, etc.

Usando los conceptos descritos para abrir un archivo de audio .wav, realice en python lo siguiente:

a) Codificador: Realice la codificación en ∑Δ para el audio del ejemplo, y crear el archivo correspondiente al resultado.

b) Decodificador: Reconstruya la señal de audio a partir del archivo del literal anterior, de ∑Δ a .wav, y pruebe su resultado ejecutando el archivo con un programa como windows media player.

c) Realice las observaciones correspondientes al proceso realizado.

Trabajo extra, opcional

d) Cree un archivo de audio en formato .wav dictando una frase como la mostrada, y repita el proceso anterior.

e) Realice las observaciones correspondientes al proceso realizado.

---

Codificador Sigma-Delta

Se adjunta un algoritmo en python de referencia al que hay que añadir la parte de manejo del audio.

– En el bloque de ingreso complete las instrucciones para leer el archivo. Observe los nombres de las variables.

# Modulacion Delta - Codificador de audio
# entrada x(t), salida: ysalida[n]
# propuesta: edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves
import scipy.signal as senal

# INGRESO
# archivo=......
# fsonido, sonido = ......

# PROCEDIMIENTO

# Analógica de referencia
deltaT  = 1/(2*np.pi*fsonido)
xanalog = sonido[:,0] # Canal izquierdo
xmax    = np.max(xanalog)
nsonido = len(xanalog)
t0 = 0
tn = nsonido*deltaT
t  = np.arange(0,tn,deltaT)

# Codificacion Sigma-Delta
salto  = 1 #usa todas las muestras sin saltar
deltaY = xmax//10
nd = nsonido//salto
td = np.arange(0,nd,1) # eje tiempo[n] digital
xdigital = np.zeros(nd,dtype=float)
ysalida  = np.zeros(nd,dtype=int)
muestra  = xanalog[0]
i = 1
while not(i >= nd):
    muestra = xanalog[i*salto] # referencia analógica
    diferencia = muestra-xdigital[i-1]
    if (diferencia>0):
        bit = 1
    else:
        bit = -1
    xdigital[i] = xdigital[i-1]+bit*deltaY
    ysalida[i]  = bit
    i = i + 1
fsalida = fsonido/salto
parametros = np.array([deltaT,deltaY,fsalida])

# SALIDA
print(ysalida)
print(parametros)

# Graba archivo
np.savetxt('sigmadelta_datos.txt',ysalida,fmt='%i')
np.savetxt('sigmadelta_parametros.txt',parametros)

# Grafico
# Escala y RANGO ejex del gráfico
a = int(nsonido*0.35)
b = int(nsonido*0.355)

plt.figure(1)       # define la grafica
plt.suptitle('Codificador Sigma-Delta Audio.wav')

# grafica de 3x1 y subgrafica 1
plt.subplot(311)
plt.ylabel('x(t)')
# rango en el eje y
xmax = np.max(xanalog)+0.1*np.max(xanalog)
xmin = np.min(xanalog)-0.1*np.max(xanalog)
plt.axis((a*deltaT, b*deltaT, xmin, xmax))
plt.plot(t[a:b],xanalog[a:b], 'g')
plt.ylabel('xanalogica[n]')

# grafica de 3x1 y subgrafica 2
plt.subplot(312) 
plt.ylabel('xdigital[n]')
# rango en el eje
mxa=np.max(xdigital[a:b])
mna=np.min(xdigital[a:b])
plt.axis((a,b,mxa,mna))
#plt.plot(td,xdigital,'bo')
plt.step(td[a:b],xdigital[a:b], where='post',color='m')

# grafica de 3x1 y subgrafica 3
plt.subplot(313) 
plt.ylabel('ysalida[n]')
plt.axis((a,b,-1.1,1.1))
plt.step(td[a:b],ysalida[a:b], where='post',color='b')
plt.show()

---

Decodificador Sigma-Delta

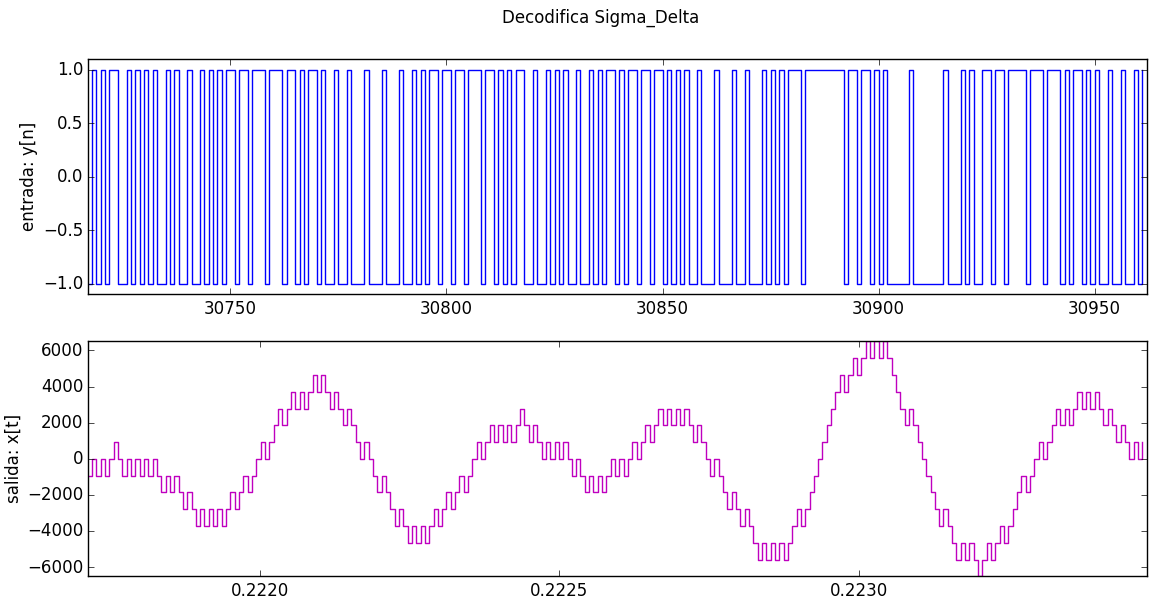
El resultado gráfico al decodificar el archivo de ∑Δ se muestra, se debe añadir la instrucción para generar el archivo de audio y poder escucharlo.

modifique la seccion de #Salida para crear el arhivo de audio con nombre: ‘sigmadeltaaudio.wav’.

# Modulacion Sigma-Delta Decodificador
# entrada yentrada[n], salida: x[t]
# propuesta:edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as waves

# INGRESO
archivodatos = 'sigmadelta_datos.txt'
archivoparam = 'sigmadelta_parametros.txt'

# PROCEDIMIENTO
# lectura de archivo
yentrada = np.loadtxt(archivodatos,dtype=int)
datos    = np.loadtxt(archivoparam,dtype=float)
deltaD   = datos[0]
deltaY   = datos[1]
fsonido  = datos[2]
# muestras para gráfica
k = len(yentrada) 

# Arreglos para datos
xdigital = np.zeros(k, dtype='int16')
punto    = np.zeros(k, dtype=int)
td       = np.zeros(k, dtype=float) # eje n digital

# calcula los valores para digital
xdigital[0] = yentrada[0]
punto[0] = 0
td[0]    = 0
for i in range(1,k):
    punto[i] = i
    td[i]    = deltaD*i
    xdigital[i] = xdigital[i-1]+yentrada[i]*deltaY

# SALIDA
print(xdigital)
#Archivo de audio
# CREAR EL ARCHIVO DE AUDIO ***********************

#Gráfico
a = int(k*0.25) # RANGO ejex del gráfico
b = int(k*0.252)

plt.figure(1) # define la grafica
plt.suptitle('Decodifica Sigma_Delta')

plt.subplot(211) # grafica de 2x1 y subgrafica 1
plt.ylabel('entrada: y[n]')
plt.axis((a,b,-1.1,1.1))
#plt.plot(punto[a:b],yentrada[a:b],'b')
plt.step(punto[a:b],yentrada[a:b], where='post', color='b')

plt.subplot(212) # grafica de 2x1 y subgrafica 2
plt.ylabel('salida: x[t]')
xmax = np.max(xdigital[a:b]) # rango en el eje
xmin = np.min(xdigital[a:b])
plt.axis((a*deltaD,b*deltaD,xmin,xmax))
#plt.plot(td[a:b],xdigital[a:b],'m')
plt.step(td[a:b],xdigital[a:b], where='post', color='m')
plt.show()

La gráfica muestra solo el intervalo de tiempo entre a=0.25 y b=0.252 del total de tiempo del audio, el propósito es la observacion visual complementará a la de escuchar el audio resultante.