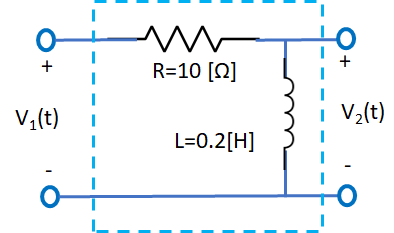
Ejercicio: 3Eva2016TI_T3 LTI CT Circuito RL respuesta de frecuencia
a. Determinar su función de transferencia
voltaje en la entrada,
v_1(t) = v_R(t) + v_L(t) v_1(t) = R i(t) + v_L(t)voltaje en la salida,
v_2(t) = L \frac{\delta}{\delta t}i(t)
sustituyendo i(t)en la ecuacion de v1
v_1(t) = R \frac{1}{L} \int_{-\infty}^{t}v_2(\tau) \delta \tau + v_L(t)usando un solo operador, el diferencial,
\frac{\delta}{\delta t} v_1(t) = \frac{R}{L} v_2(t) + \frac{\delta}{\delta t} v_2(t)cambiando al dominio de frecuencia ω
j\omega V_1(\omega) = \frac{R}{L} V_2(\omega) + j\omega V_2(\omega) j\omega L V_1(\omega) = R V_2(\omega) + j\omega L V_2(\omega) j\omega L V_1(\omega) = V_2(\omega)\Big( R + j\omega L \Big) H(\omega) = \frac{V_2(\omega)}{V_1(\omega)} = \frac{j\omega L}{ R + j\omega L } H(\omega) = \frac{j\omega \frac{L}{R}}{ 1 + j\omega \frac{L}{R} }usando los valores del circuito
H(\omega) = \frac{j\omega 0.2}{ 10 + j\omega 0.2 } H(\omega) = \frac{j\omega}{50 + j\omega } |H(\omega)| = \frac{|\omega|}{\sqrt{ 50^2 + \omega^2} } \theta_{H(\omega)} = \frac{\pi}{2} - \arctan \Big( \frac{\omega}{50}\Big) \omega_0 = \frac{R}{L} = \frac{10}{0.2} = 50 rad/sb. Determinar, esquematizar y etiquetar su respuesta de frecuencia, indicando a que tipo de filtro no ideal de frecuencias selectivas se podría asociar su comportamiento.
tarea…
c. Obtener la respuesta impulso h(t) que representa al circuito eléctrico.
h(t) = \mathscr{F} ^{-1} \Big[ H(\omega) \Big] = \mathscr{F} ^{-1} \Big[ \frac{j\omega}{50 + j\omega } \Big]separando en fracciones parciales y usando la tabla de transformadas de Fourier:
= \mathscr{F} ^{-1} \Big[ 1-\frac{50}{50 + j\omega } \Big] h(t) = \delta (t) - 50 e^{-50t} \mu (t)d. Determinar la respuesta v2(t) que se obtiene a la salida de dicho sistema cuando tiene una entrada v1(t) = sen 50t [V].
¿Qué puede decir acerca de si el sistema transmite con distorsión o sin distorsión? Justifique su respuesta de manera razonada.
Los términos con impulso desplazados tienen magnitud solo en las posiciones donde el impulso tiene valor 1. En este caso es con ω=±50
V_2(\omega) =\pi \Big( \delta (\omega+50) \frac{(-1)(-50)}{50 - j50 } - \delta (\omega-50) \frac{(-1)50}{50 + j50}\Big)dividiendo el numerador y denominador para 50 se simplifica a
=\pi \Big( \delta (\omega+50) \frac{1}{1 - j1 } + \delta (\omega-50) \frac{1}{1 + j1}\Big)multiplicando el primer coeficiente por 1+j y el segundo coeficiente por 1-j, se convierte el denominador en un número real.
=\pi \Big( \delta (\omega+50) \frac{1(1+j)}{(1 - j1) (1+j)} + \delta (\omega-50) \frac{1(1-j)}{(1 + j1)(1-j)}\Big) =\pi \Big( \delta (\omega+50) \frac{1+j}{2} + \delta (\omega-50) \frac{1-j}{2}\Big) =\frac{\pi}{2} \Big( \delta (\omega+50)+j\delta (\omega+50) + \delta (\omega-50) - j\delta (\omega-50) \Big) V_2(\omega) =\frac{\pi}{2} \Big( \delta (\omega+50) + \delta (\omega-50)\Big) + j\frac{\pi}{2} \Big(\delta (\omega+50)- \delta (\omega-50) \Big)obteniendo v2(t) en el dominio de tiempo,
v_2(t) = \mathscr{F}^{-1} \Big[V_2(\omega) \Big] =\frac{1}{2} \mathscr{F}^{-1} \Bigg[ \pi \Big(\delta (\omega+50) + \delta (\omega-50) \Big )\Bigg] + +\frac{1}{2} \mathscr{F}^{-1} \Bigg[ j\pi \Big(\delta (\omega+50) + \delta (\omega-50) \Big )\Bigg] v_2(t) =\frac{1}{2} \cos(50t) + \frac{1}{2} \sin(50t)por magnitud y fase, simplificación trigonométrica
v_2(t) =\frac{1}{\sqrt{2}} \sin\Big(50t+\frac{\pi}{4}\Big)también con Sympy,
>>> v2=(1/2)*sym.cos(50*t)+(1/2)*sym.sin(50*t) >>> sym.trigsimp(v2) 0.5*sqrt(2)*sin(50*t + pi/4) >>>
el resultado es concordante con lo que realiza la función de transferencia, respuesta al impulso H(ω) en ω=50
|H(\omega)| = \frac{|\omega|}{\sqrt{ 50^2 + \omega^2} } = \frac{|50|}{\sqrt{ 50^2 + 50^2} } = \frac{|50|}{\sqrt{ 2(50^2)} } = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \theta_{H(\omega)} = \frac{\pi}{2} - \arctan \Big( \frac{\omega}{50}\Big) = \frac{\pi}{2} - \arctan \Big( \frac{50}{50}\Big) = \frac{\pi}{2}-\frac{\pi}{4} = \frac{\pi}{4}considerando también que:
\omega_0 = \frac{R}{L} = \frac{10}{0.2} = 50 rad/s