Publicado en por Edison Del Rosario

5.3 LTI-CT Fourier – H(ω) Funciones de transferencia

Referencia: Oppenheim 3.2 p182, 4.4 p314, Lathi p714 Hsu 5.5.A p223

Las transformadas de Fourier presentan una facilidad con la propiedad de la convolución expresada como:

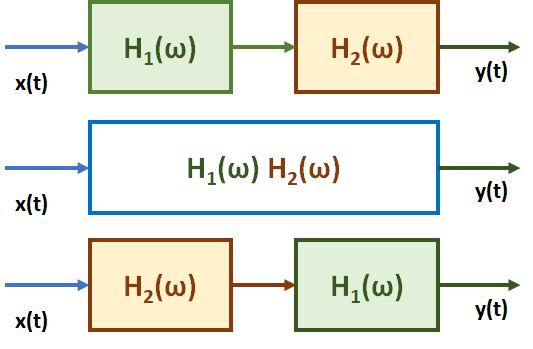
y(t)=h(t)⊛x(t)↔Y(ω)=H(ω)X(ω) y(t)= h(t) \circledast x(t) \leftrightarrow Y(\omega) = H(\omega) X(\omega)

Lo que para señales y sistemas representa un componente importante en el análisis de sistemas LTI, al poder representar los sistemas por bloques en serie y paralelo semejante a lo realizado con la transformada de Laplace:

LIT CT Bloques Serie

La convergencia de la transformada de Fourier se garantiza bajo ciertas condiciones. El análisis de Fourier para el estudio de sistemas LTI se restringe a los que sus respuestas al impulso tienen transformada de Fourier. Los detalles se mostrarán en cada ejercicio presentado.

Ejemplo 1. H(ω) desde una ecuación diferencial

Referencia: Oppenheim Ej 4.25 p331

Considere un sistema LTI estable que se caracteriza por la ecuación diferencial,

δ2δt2y(t)+4δδty(t)+3y(t)=δδtx(t)+2x(t) \frac{\delta^2}{\delta t^2}y(t) + 4\frac{\delta}{\delta t} y(t) + 3 y(t) = \frac{\delta}{\delta t}x(t)+2x(t)

usando la propiedad de la diferenciación en el dominio ω, se tiene que:

(jω)2Y(ω)+4(jω)Y(ω)+3Y(ω)=(jω)X(ω)+2X(ω) (j\omega)^2 Y(\omega) + 4(j\omega) Y(\omega) + 3 Y(\omega) = (j\omega)X(\omega)+2X(\omega) ((jω)2+4(jω)+3)Y(ω)=((jω)+2)X(ω) \Big((j\omega)^2 + 4(j\omega) + 3\Big) Y(\omega) = \Big((j\omega)+2\Big) X(\omega)

la función de transferencia se obtiene como,

H(ω)=Y(ω)X(ω) H(\omega) = \frac{Y(\omega)}{X(\omega)} H(ω)=(jω)+2(jω)2+4(jω)+3 H(\omega) = \frac{(j\omega)+2}{(j\omega)^2 + 4(j\omega) + 3}

Para facilitar encontrar h(t) se usan fracciones parciales respecto a jω, de forma semejante a lo realizado para el dominio s con instrucciones de Sympy-Python, Las instrucciones las puede recordar observando el ejercicio 2, donde se adjunta el algoritmo.

Hw:
(jw+2)/(jw**2+4*jw+3)
Hw en fracciones parciales:
    1            1     
---------- + ----------
2*(jw + 3)   2*(jw + 1)

con la tabla de transformadas de Fourier se obtiene que,

h(t)=12e−tμ(t)+12e−3tμ(t) h(t) = \frac{1}{2} e^{-t} \mu(t) + \frac{1}{2} e^{-3t} \mu(t)

Ejemplo 2. respuesta total Y(ω)=X(ω)H(ω)

Referencia: Oppenheim Ej 4.27 p332

Considere el sistema del ejemplo anterior y suponga una entrada x(t) dada por

x(t)=e−tμ(t) x(t) = e^{-t} \mu(t) X(ω)=1jω+1 X(\omega) = \frac{1}{j\omega +1}

la salida del sistema usando los componentes en el dominio de la frecuencia

Y(ω)=H(ω)X(ω) Y(\omega) = H(\omega)X(\omega) =[jω+2(jω+1)(jω+3)][1jω+1] = \Big[ \frac{j\omega+2}{(j\omega+1)(j\omega + 3)} \Big]\Big[\frac{1}{j\omega +1}\Big] =jω+2(jω+1)2(jω+3) = \frac{j\omega+2}{(j\omega+1)^2 (j\omega + 3)}

separando en fracciones parciales

Hw:
          jw + 2         
-------------------------
         /  2           \
(jw + 1)*\jw  + 4*jw + 3/

Hw fracciones parciales jw:
      1            1             1     
- ---------- + ---------- + -----------
  4*(jw + 3)   4*(jw + 1)             2
                            2*(jw + 1) 
>>>

con la tabla de transformadas de Fourier se obtiene que,

y(t)=[14e−t+12te−t−14e−3t]μ(t) y(t) = \Big[ \frac{1}{4} e^{-t} +\frac{1}{2}te^{-t} - \frac{1}{4} e^{-3t} \Big] \mu (t)

Instrucciones en Python

# H(w) Funciones de transferencia
# blog.espol.edu.ec/telg1001/
import sympy as sym

# INGRESO
w = sym.Symbol('w', real=True)
j = sym.I
jw = sym.Symbol('jw',real=True)

Xw = 1/(jw+1)
Hw = (jw+2)/(jw**2+4*jw+3)

# PROCEDIMIENTO
Yw = Hw*Xw
Ywp = sym.apart(Yw,jw)

print('Hw:')
sym.pprint(Yw)
print('\nHw fracciones parciales jw:')
sym.pprint(Ywp)

Ejemplo 3. y(t) con h(t) y x(t) en dominio de frecuencia

Referencia: Oppenheim Ej 4.19 p320,  Hsu 5.4.I p220

Considere la respuesta al impulso de un sistema LTI como:

h(t)=e−atμ(t) , a>0 h(t) = e^{-at} \mu (t) \text{ , } a>0

y una señal de entrada:

x(t)=e−btμ(t) , b>0 x(t) = e^{-bt} \mu (t) \text{ , } b>0

En lugar de calcular la convolución se resolverá el problema en el dominio de la frecuencia.

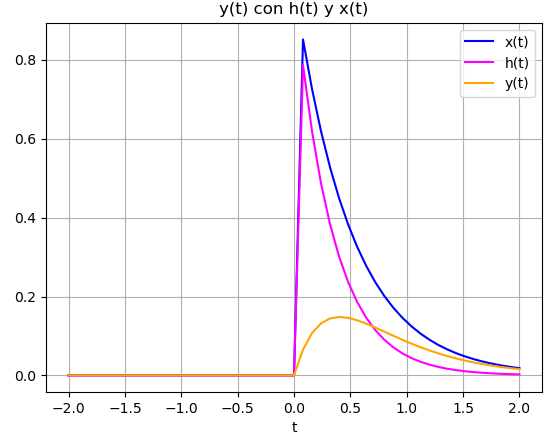
Para observar una gráfica, se supondrán valores de a=3 y b=2

H(ω)=1a+jω H(\omega) = \frac{1}{a+ j \omega} X(ω)=1b+jω X(\omega) = \frac{1}{b+ j \omega} Y(ω)=H(ω)X(ω)=[1a+jω][1b+jω] Y(\omega) = H(\omega)X(\omega) = \Big[ \frac{1}{a+ j \omega} \Big] \Big[ \frac{1}{b+ j \omega} \Big]

Para hacer la transformada inversa de Fourier, se usa fracciones parciales, semejante a lo realizado en la unidad 4

Y(ω)=k1a+jω+k2b+jω Y(\omega) = \frac{k_1}{a+ j \omega} + \frac{k_2}{b+ j \omega} k1=1(a+jω)(b+jω)∣jω=−a=1b−a k_1 = \frac{1}{\cancel{(a+ j \omega)} (b+ j \omega)} \Big|_{j\omega=-a} = \frac{1}{b-a} k2=1(a+jω)(b+jω)∣jω=−b=1a−b k_2 = \frac{1}{(a+ j \omega) \cancel{(b+ j \omega)}} \Big|_{j\omega=-b} = \frac{1}{a-b}

con lo que k1= -k2

Y(ω)=1b−a[1a+jω−1b+jω] Y(\omega) = \frac{1}{b-a} \Big[\frac{1}{a+ j \omega} - \frac{1}{b+ j \omega} \Big]

la transformada inversa se obtiene para cada término de la suma como:

y(t)=1b−a[e−atμ(t)−e−btμ(t)] y(t) = \frac{1}{b-a} \Big [ e^{-at} \mu(t) - e^{-bt} \mu(t) \Big]

Resultado usando el algoritmo del ejercicio 3

 Y(w) = H(w)*X(w)
         1         
-------------------
(a + I*w)*(b + I*w)

 Y(w) en fracciones parciales:
        1                   1        
----------------- - -----------------
(a - b)*(b + I*w)   (a - b)*(a + I*w)

Ejemplo 4. h(t) como respuesta a un impulso desplazado

Referencia: Oppenheim Ej 4.16 p317, Lathi 7.14 708. Hsu 5.4.B p219

Considere un sistema LTI CT (continuo en el tiempo) con respuesta a impulso dado por:

h(t)=δ(t−t0) h(t) = \delta (t-t_0)

La respuesta a este sistema esta dada por la respuesta desplazada del impulso.

H(ω)=1e−jωt0=e−jωt0 H(\omega) = 1 e^{-j \omega t_0} = e^{-j \omega t_0}

El sistema ante una entrada x(t) con transformada de Fourier X(ω) tendrá la salida:

Y(ω)=H(ω)X(ω)=e−jωt0X(ω) Y(\omega) =H(\omega)X(\omega) = e^{-j \omega t_0} X( \omega)

resultado con algoritmo Python

 h(t):
DiracDelta(-a + t)

 H(w):
 -I*a*w
e      
>>>

Instrucciones en Python

# H(w) Funciones de transferencia
# blog.espol.edu.ec/telg1001/
import sympy as sym

# INGRESO
t = sym.Symbol('t', real=True,)
w = sym.Symbol('w', real=True)
j = sym.I
a = sym.Symbol('a', real=True,positive=True)
u = sym.Heaviside(t)
d = sym.DiracDelta(t)

#ht = d
ht = d.subs(t,t-a)
#ht = sym.exp(-a*sym.Abs(t))
#ht = u.subs(t,t+a)-u.subs(t,t-a)
#ht = sym.exp(-a*t)*u

# PROCEDIMIENTO
ht = sym.expand(ht)  # expresion de sumas
Hw = sym.fourier_transform(ht,t,w/(2*sym.pi))

# SALIDA
print('\n h(t):')
sym.pprint(ht)
print('\n H(w):')
sym.pprint(Hw)

Ejemplo 5. h(t) de un exponencial decreciente

Referencia: Oppenheim Ejercicio 4.1. p290, Lathi ejemplo 7.1 p685, Hsu Ejemplo 5.2 p218

x(t)=e−atμ(t) ; a>0 x(t) =e^{-at} \mu (t) \text{ ; } a \gt 0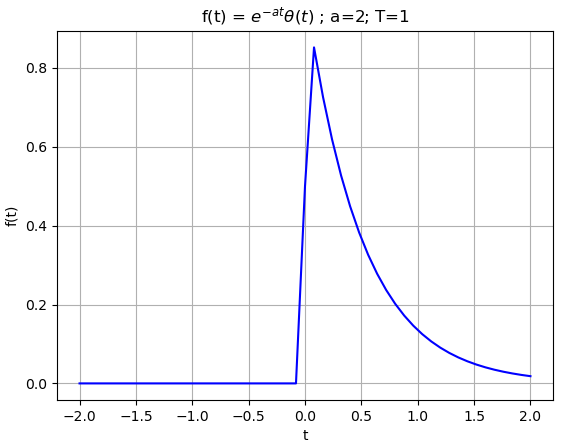


realizado con el algoritmo anterior, se puede comprobar el resultado con la tabla de transformadas de Fourier

 h(t):
 -t              
 ---             
  2              
e   *Heaviside(t)

 H(w):
    2    
---------
2*I*w + 1
>>>

Ejemplo 6. h(t) como un diferenciador

Referencia: Oppenheim Ej 4.16 p317, Lathi 7.14 716. Hsu 5.4.G p220

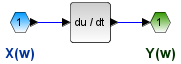
El bloque de respuesta a impulso es un diferenciador, por lo que las funciones de entrada y salida se relacionan por

y(t)=δδtx(t) y(t) = \frac{\delta}{\delta t}x(t)

usando la diferenciación de las propiedades de la transformada de Fourier

Y(ω)=jωX(ω) Y(\omega) = j \omega X( \omega )

en consecuencia:

H(ω)=jω H(\omega) = j \omega

Ejemplo 7. h(t) como un integrador

Referencia: Oppenheim Ej 4.17 p318,  Hsu 5.4.I p220

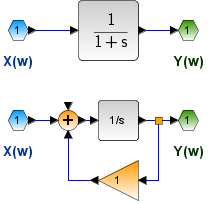
El bloque de respuesta a impulso es una integración, por lo que las funciones de entrada y salida se relacionan por

y(t)=∫−∞tx(τ)δτ y(t) = \int_{-\infty}^{t}x(\tau) \delta \tau

usando la propiedad de Integración:

H(ω)=1jω+πδ(ω) H(\omega) = \frac{1}{j \omega} +\pi \delta(\omega) Y(ω)=[1jω+πδ(ω)]X(ω) Y(\omega) = \Big[\frac{1}{j \omega} +\pi \delta(\omega) \Big]X( \omega) Y(ω)=1jωX(ω)+πδ(ω)X(0) Y(\omega) = \frac{1}{j \omega}X(\omega) +\pi \delta(\omega) X(0)