Considere la exponencial compleja discreta con frecuencia (ω0 + 2π)
e^{j(\omega _0 + 2 \pi)n} =e^{j 2 \pi n} e^{j \omega _0 n} = e^{j \omega _0 n}Se puede ver que la exponencial con frecuencia ω0 + 2π es la misma que aquella con la frecuencia ω0.
Existe una situación diferente en el caso contínuo, en el cual las señales ejω0t son todas distintas para distintos valores de ω0.
En el caso discreto, éstas señales no son distintas, ya que la señal con frecuencia ω0 es idéntica a las señales con frecuencias ω0 ± 2π , ω0 ± 4π, … y las que le siguen. Por lo tanto, al considerar las exponenciales complejas, necesitamos tomar en cuenta solamente un intervalo de frecuencia de longitud 2π dentro del cual se escoge ω0.
ω0N = 2π m
o de otra forma
ω0/2π = m/N
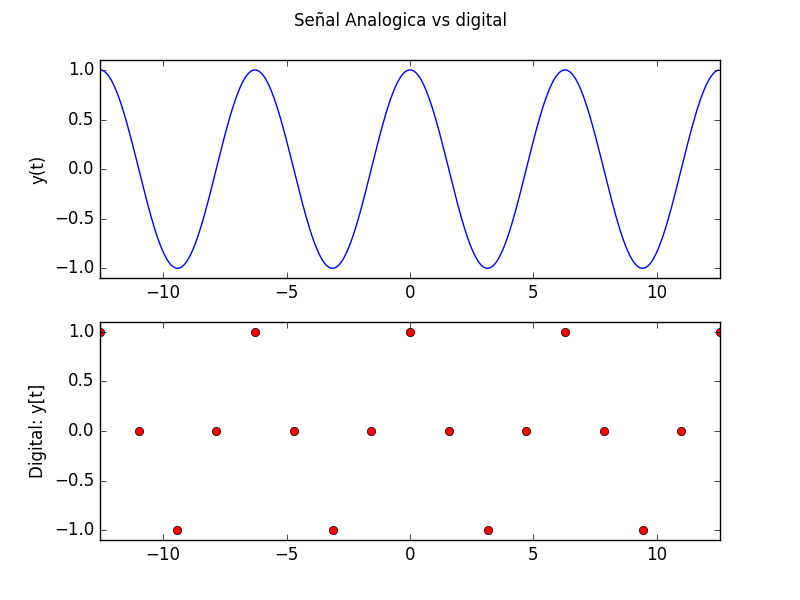
Para el caso de m=1 y N=2
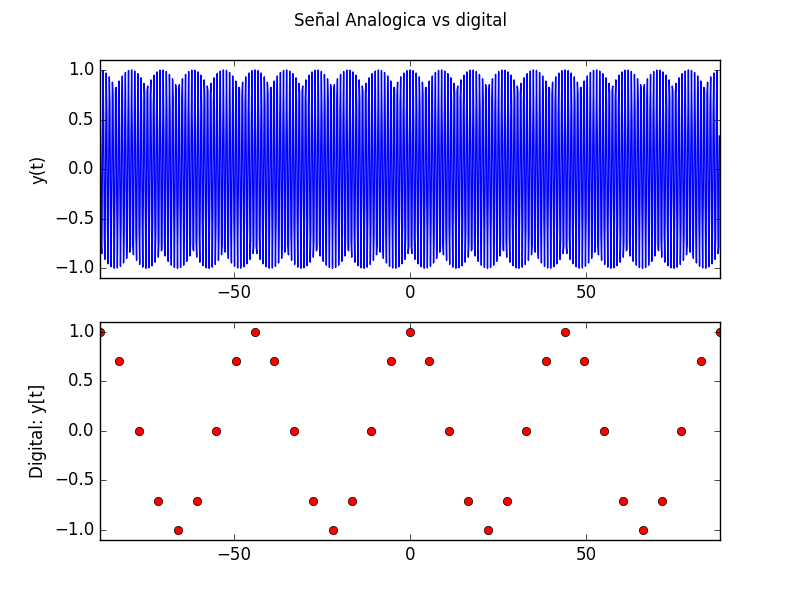
otra prueba con m=7 y N=4
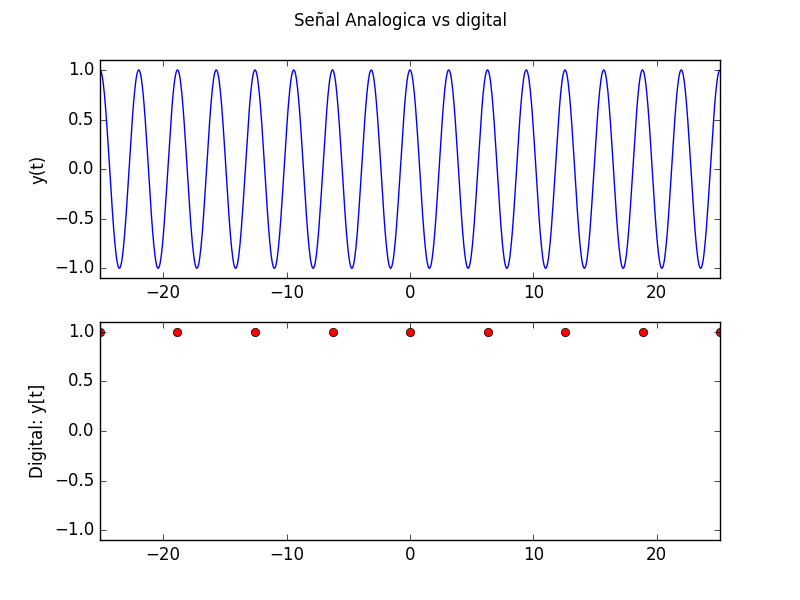
con m=2 y N=1
El código en python para realizar las gráficas es:
# Señales discretas, y(t) a y[t] # propuesta:edelros@espol.edu.ec import numpy as np import math import matplotlib.pyplot as plt # Definir la funcion para el ejemplo def analogica(f,t): # función matemática CAMBIAR AQUI y=np.cos(f*t) return(y) # Programa para graficar la función # INGRESO rango = 4 # float(input('rangos en periodos de analogica:')) m = 1 # float(input('frecuencia de analógica:')) N = 2 # float(input('frecuencia digital:')) # PROCEDIMIENTO # grafica analogica puntoscontinuos = 500 t0 = -rango*2*np.pi*m/2 tn = rango*2*np.pi*m/2 t = np.linspace(t0,tn,puntoscontinuos+1) yanalog = analogica(m,t) # grafica digital deltaD = (2*np.pi*m)/(2*N) muestreo = int((tn-t0)//deltaD +1) td = np.linspace(t0,tn,muestreo) ydigital = analogica(m,td) # SALIDA - GRAFICA #Escala y para el grafico margen = 0.1*np.max(yanalog) ymax = np.max(yanalog)+margen ymin = np.min(yanalog)-margen plt.figure(1) plt.suptitle('Señal Analogica vs digital') plt.subplot(211) # grafica de 2x1 arriba plt.plot(t,yanalog) plt.axis((t0,tn,ymin,ymax)) plt.ylabel('y(t)') plt.subplot(212) # grafica de 2x1 abajo plt.plot(td,ydigital,'ro') plt.axis((t0,tn,ymin,ymax)) plt.ylabel('Digital: y[t]') plt.show()