Referencia: 1Eva2010TII_T3 LTI CT H(s) de bloques en paralelo y retraso
El diagrama de bloques del sistema consta de dos sistema de primer orden en paralelo y el resultado en serie con un bloque retraso en tiempo.
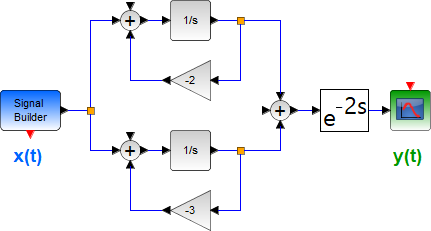La ecuación de respuesta a impulso H(s), siguiendo el diagrama se presenta como:
literal a
Para el desarrollo analítico se simplifica el problema, separando el bloque de atraso para el final, dado que el sistema es LTI los desplazamietos en el tiempo de la entrada tendrán semejante respuesta en la salida.
La función de transferencia H(s) o respuesta al impulso será:
H(s) =\Big[ H_1(s)\Big] e^{-2s} H_1(s) = \frac{1}{s+2}+\frac{1}{s+3}Los componentes por ser de primer orden y estar en paralelo, no se requiere aplicar fracciones parciales.
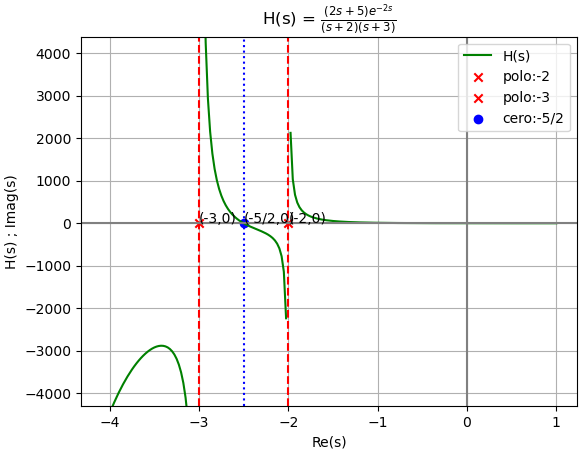
Los polos del sistema se encuentran en el lado izquierdo del plano, por lo que sus componentes en el tiempo son decrecientes.
{polos,veces}: {-2: 1, -3: 1}
polos reales: 2 complejos: 0
sobre lado derecho RHP: 0
sobre Eje Imaginario, repetidos: 0 unicos: 0
asintoticamente: estable
NO existen polos en el lado derecho del plano, por lo que el sistema es asintoticamente estable, en consecuencia BIBO estable.
literal b
Para la transformada inversa de Laplace, se recuerda que se tiene un componente de retraso en cascada, por lo que se ajusta H(s)*retraso en fracciones parciales, se presentan dos componentes:
h(t) : 4 - 2*t 6 - 3*t e *Heaviside(t - 2) + e *Heaviside(t - 2)
que tienen la forma decreciente de la función, Para la gráfica sympy usa como θ(t)=μ(t)=Heaviside(t)
literal c
A partir del diagrama de bloques se tiene:
H(s) =\frac{Y(s)}{X(s)}= \Big[ \frac{2s+5}{s^2+5s+6} \Big] e^{-2s} (s^2+5s+6)Y(s)=(2s+5)e^{-2s} X(s) s^2Y(s)+5sY(s)+6Y(s)=(2sX(s)+5X(s))e^{-2s}que al convertir al dominio del tiempo se escribe como:
\frac{\delta^2}{\delta t^2}y(t)+5\frac{\delta}{\delta t}y(t)+6y(t)=2\frac{\delta}{\delta t}x(t-2)+5x(t-2)literal d
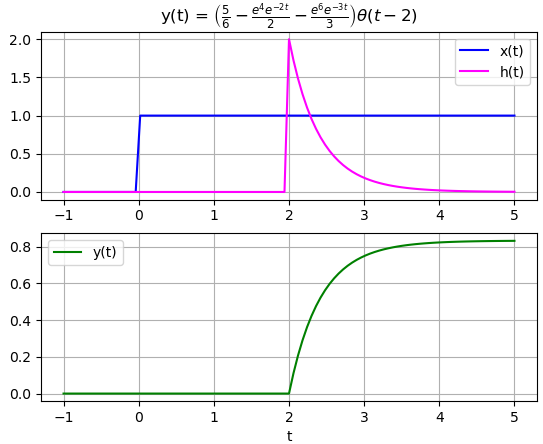
la respuesta ante la entrada escalon requiere que x(t) = μ(t), no se especifican condiciones iniciales del problema, por lo que se asumen iguales a cero. De la tabla de transformadas se obtiene X(s) = 1/s
H(s) =\Big[ \frac{1}{s+2}+\frac{1}{s+3} \Big] e^{-2s} Y(s) = H(s)X(s) =\Big[ \frac{1}{s+2}+\frac{1}{s+3} \Big] e^{-2s} \frac{1}{s}que separando en fracciones parciales se convierte en:
Y(s) =\Big[\frac{5/6}{s} -\frac{1/3}{s+3}-\frac{1/2}{s+2} \Big] e^{-2s} y(t) =\Big[\frac{5}{6} -\frac{1}{3}e^{-3(t-2)}-\frac{1}{2}e^{-2(t-2)}\Big] \mu (t-2)el resultado usando algoritmos es:
H(s) = P(s)/Q(s):
/ 1 1 \ -2*s
|----- + -----|*e
\s + 3 s + 2/
H(s) en factores:
-2*s
(2*s + 5)*e
---------------
(s + 2)*(s + 3)
h(t) :
/ 4 -2*t 6 -3*t\
\e *e + e *e /*Heaviside(t - 2)
polosceros:
exp(-2*s) : {'Q_polos': {-2: 1, -3: 1}, 'P_ceros': {-5/2: 1}, 'Hs_k': (2*s + 5)/((s + 2)*(s + 3))}
Q_polos : {-2: 1, -3: 1}
P_ceros : {-5/2: 1}
Estabilidad de H(s):
n_polos_real : 2
n_polos_imag : 0
enRHP : 0
unicos : 0
repetidos : 0
asintota : estable
X(s):
1
-
s
Respuesta entrada cero ZIR H(s) y condiciones iniciales
term_cero : 0
ZIR :
0
yt_ZIR :
0
ZSR respuesta estado cero:
ZSR :
/ 1 1 5 \ -2*s
|- --------- - --------- + ---|*e
\ 3*(s + 3) 2*(s + 2) 6*s/
yt_ZSR :
/ 4 -2*t 6 -3*t\
|5 e *e e *e |
|- - -------- - --------|*Heaviside(t - 2)
\6 2 3 /
Y(s)_total = ZIR + ZSR:
/ 1 1 5 \ -2*s
|- --------- - --------- + ---|*e
\ 3*(s + 3) 2*(s + 2) 6*s/
y(t)_total = ZIR + ZSR:
/ 4 -2*t 6 -3*t\
|5 e *e e *e |
|- - -------- - --------|*Heaviside(t - 2)
\6 2 3 /
>>>
Instrucciones en Python
Usando los bloques desarrollados en la y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta.
# Y(s) Respuesta total con entada cero y estado cero # Qs Y(s) = Ps X(s) ; H(s)=Ps/Qs # http://blog.espol.edu.ec/telg1001/ import sympy as sym import matplotlib.pyplot as plt import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) d = sym.DiracDelta(t) u = sym.Heaviside(t) # H(s) y estabilidad Hs = (1/(s+2)+1/(s+3))*sym.exp(-2*s) #Hs = 1+0*s cuando es constante # X(s) Señal de entrada xt = u # condiciones iniciales, [y'(0),y(0)] orden descendente t0 = 0 cond_inicio = [0, 0] # estado cero no se usan # Grafica, intervalo tiempo [t_a,t_b] t_a = -1 ; t_b = 5 muestras = 101 # 51 resolucion grafica # PROCEDIMIENTO Hs = fcnm.apart_s(Hs) # fracciones parciales Hs_fc = fcnm.factor_exp(Hs) # en factores Hs_Qs2 = fcnm.Q_cuad_s_parametros(Hs_fc) polosceros = fcnm.busca_polosceros(Hs) Q_polos = polosceros['Q_polos'] P_ceros = polosceros['P_ceros'] estable = fcnm.estabilidad_asintotica_s(Q_polos) # H(t) respuesta al impulso ht = 0*s term_suma = sym.Add.make_args(Hs) for term_k in term_suma: ht_k = sym.inverse_laplace_transform(term_k,s,t) # simplifica log(exp()) ej: e**(-2s)/(s**2) if ht_k.has(sym.log): ht_k = sym.simplify(ht_k,inverse=True) ht = ht + ht_k lista_escalon = ht.atoms(sym.Heaviside) ht = sym.expand(ht,t) # terminos suma ht = sym.collect(ht,lista_escalon) # PROCEDIMIENTO Respuesta ZIR, ZSR Xs = fcnm.laplace_transform_suma(xt) # ZIR_s respuesta entrada cero de s sol_ZIR = fcnm.respuesta_ZIR_s(Hs,cond_inicio) ZIR = sol_ZIR['ZIR'] yt_ZIR = sol_ZIR['yt_ZIR'] # ZSR respuesta estado cero, Y(s) a entrada X(s) sol_ZSR = fcnm.respuesta_ZSR_s(Hs,Xs) ZSR = sol_ZSR['ZSR'] yt_ZSR = sol_ZSR['yt_ZSR'] # Respuesta total Y(s) y y(t) Ys = ZIR + ZSR Ys = fcnm.apart_s(Ys) yt = yt_ZIR + yt_ZSR lista_escalon = yt.atoms(sym.Heaviside) yt = sym.collect(yt,lista_escalon) # SALIDA print(' H(s) = P(s)/Q(s):') sym.pprint(Hs) print(' H(s) en factores:') sym.pprint(Hs_fc) if len(Hs_Qs2)>0: print('\nH(s) parámetros cuadraticos:') fcnm.print_resultado_dict(Hs_Qs2) print('\n h(t) :') sym.pprint(ht) print('\npolosceros:') fcnm.print_resultado_dict(polosceros) print('\nEstabilidad de H(s):') for k in estable: print('',k,':',estable[k]) print('\n X(s): ') sym.pprint(Xs) print('\nRespuesta entrada cero ZIR H(s) y condiciones iniciales') if not(sol_ZIR == sym.nan): # existe resultado fcnm.print_resultado_dict(sol_ZIR) else: print(' insuficientes condiciones iniciales') print(' revisar los valores de cond_inicio[]') print('\n ZSR respuesta estado cero:') fcnm.print_resultado_dict(sol_ZSR) print('\n Y(s)_total = ZIR + ZSR:') sym.pprint(Ys) print('\n y(t)_total = ZIR + ZSR:') sym.pprint(yt) # Graficas polos, H(s), con polos h(t) -------- muestras_H = 201 figura_s = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,f_nombre='H',solopolos=True) figura_Hs = fcnm.graficar_Fs(Hs_fc,Q_polos,P_ceros,muestras=muestras_H,f_nombre='H') figura_ht = fcnm.graficar_ft(ht,t_a,t_b,muestras,f_nombre='h') # GRAFICAS y(t),x(t),h(t) --------------------- figura_ft = fcnm.graficar_xh_y(xt,ht,yt,t_a,t_b,muestras) plt.show()