Referencia: Oppenheim 1.6.5 p50, Lathi 1.7-2 p102, Hsu 1.5.F p18
Si el comportamiento de un sistema y sus parámetros no cambian en el tiempo, se los denomina sistemas invariantes en el tiempo.
Por ejemplo, para un circuito RC, los valores de la resistencia y capacitor fijos no varian si se realiza un experimento o medición hoy o mañana.
Expresando lo mismo como:
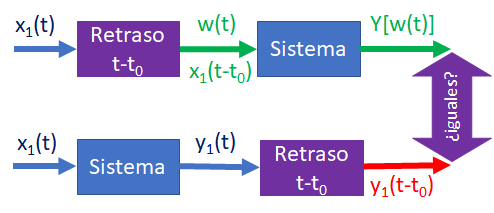
Un sistema es invariante en el tiempo si, ante un desplazamiento de tiempo en la señal de entrada, se ocasiona el mismo desplazamiento en el tiempo en la señal de salida. El resultado se repite si el desplazamiento del tiempo se aplica a la salida del sistema en lugar de la entrada.
Ejemplo 1. Sistema con comportamiento senoidal
Referencia: Oppenheim 1.14 p51
Para muestra de lo indicado, considere un sistema definido como:
y(t) = \sin[x(t)]Para revisar si es invariante en el tiempo, se debe determinar si sus propiedades de mantienen para cualquier entrada ante cualquier desplazamiento t0.
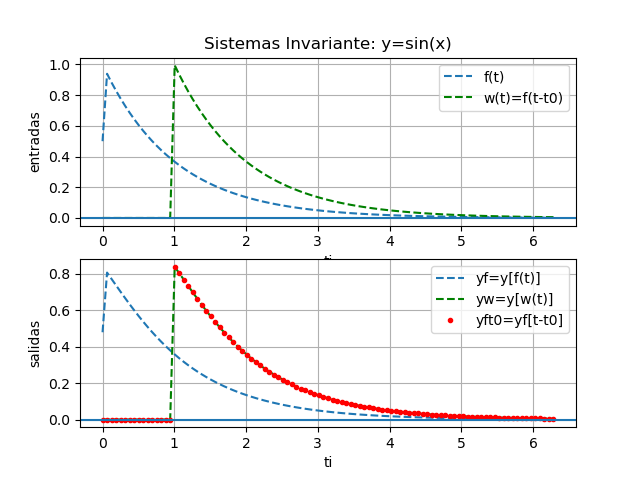
y_1 (t) = \sin[x(t - t_0)] y_2(t) = y(t - t_0)Suponga x1(t)= e(-t)u(t) la señal bajo prueba, siendo x2(t)= e(-(t-t0))u(t-t0) la entrada x1(t) desplazada en t0. Haciendo t0=1, se puede observar en la gráfica si al aplicar el retraso antes o después del sistema tienen resultados iguales.
y_1 (t) = y_2(t)
En éste caso se observa que la señal de salida se mantiene invariante en su forma y desplazada en sincronía con la señal de entrada. Por lo que el sistema es INVARIANTE en el tiempo.
La gráfica y el siguiente resultado se realizaron con el algoritmo desarrollado a partir del tema anterior sobre sistemas lineales. El algoritmo se adjunta al final.
/ -t \
yf = sin\e *Heaviside(t)/
/ -t \
yw = sin\2.71828182845905*e *Heaviside(t - 1.0)/
/ -t \
yf(t-t0) = sin\2.71828182845905*e *Heaviside(t - 1.0)/
Por otro lado, si la respuesta de la señal se modifica en el tiempo, el sistema será VARIANTE en el tiempo.
Ejemplo 2. Sistema comprime en tiempo
Referencia: Oppenheim 1.16 p52.Hsu ejercicio 1.39 p48
Considere el sistema que tiene escalamiento en el tiempo.:
y(t) = x(2t)y(t) es una versión comprimida en tiempo de x(t) en un factor de 2.
Los desplazamientos en el tiempo de la señal de entrada al pasar por el sistema también se «comprimen» por un factor de 2.
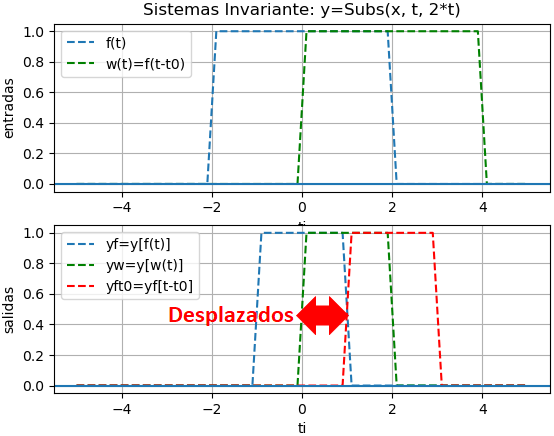
Haciendo f(t) = μ(t+2)-μ(t-2) una señal rectangular centrada en el origen con color azul en la gráfica.
Si la entrada w(t) = f(t-2)= μ(t)-μ(t-4) es una real rectangular desplazada en 2 (en color verde), su resultado en la salida se encuentra centrado en 1.
Al desplazar el resultado de la señal de entrada en su forma original en azul, por t0 se obtiene la señal de salida en color rojo. Claramente los resultados de aplicar un retraso antes o después del sistema son diferentes.
Por lo que, por ésta razón el sistema NO es invariante en el tiempo.
yf = -Heaviside(2*t - 2) + Heaviside(2*t + 2) yw = Heaviside(2*t) - Heaviside(2*t - 4.0) yft0 = -Heaviside(2*t - 6.0) + Heaviside(2*t - 2.0)
Siguiendo las indicaciones en el problema presentado, donde T se conoce como el «operador lineal«. El sistema tiene una relación de entrada-salida dada por:
y(t) = T{x(t)} = x(2t)y t0 es un desplazamiento en el tiempo.
Sea y2(t) la respuesta a x2(t) = x(t-t0) entonces:
y2(t) = T{x2(t)} = x2(2t) = x(2t-t0)
Si se desplaza el resultado de la señal de salida sin desplazar se tiene:
y(t-t0) = x(2(t-t0)) = x(2t-2t0))
y(t-t0) ≠ y2(t)
por lo que el sistema no es invariante en el tiempo.
El sistema x(2t) se conoce como compresor, pues crea una secuencia de salida cada 2 valores de la secuencia de entrada.
Ejemplo 3. Sistema multiplica por tiempo
Referencia: Oppenheim 1.13 p49, Oppenheim 1.17 p54, Hsu ejercicio 1.38 p47
Considere el siguiente sistema, cuya salida depende del intervalo de tiempo evaluado. Los desplazamientos afectan a la señal de salida.
y(t) = t x(t)Desarrollar semejante al ejercicio anterior, en forma analítica y usando Python, para la entrada:
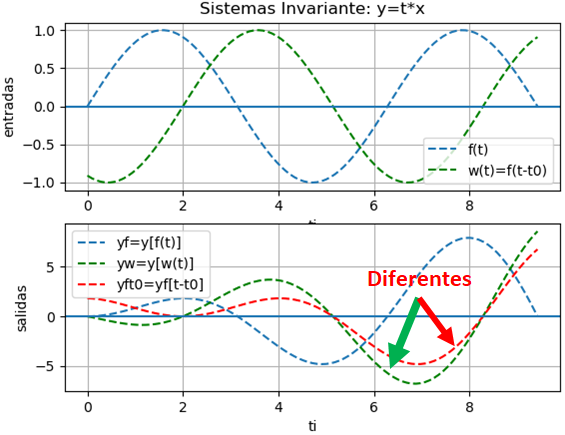
x(t) = \sin (t)
yf = t*sin(t) yw = t*sin(t - 2.0) yf(t-t0) = (t - 2.0)*sin(t - 2.0)
Para el sistema dado, al depender su magnitud de la variable t, la salida tiende a crecer con el tiempo, por lo que se puede intuir que el sistema es inestable.
Observando los resultados y la gráfica se tiene que el sistema NO es invariante en el tiempo.
Ejemplo 4. Sistema deriva la entrada
Referencia: Lathi 1.11 p103
Determine la invariabilidad de tiempo del siguiente sistema
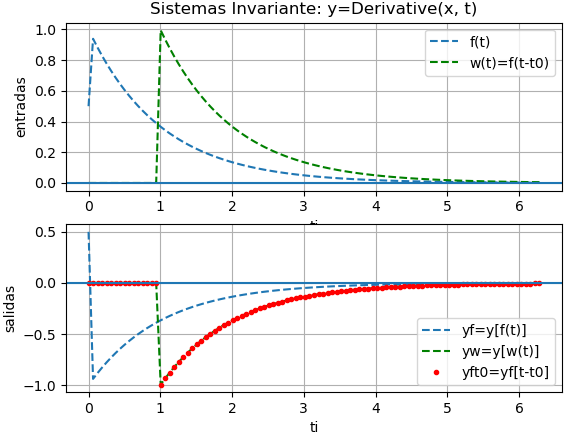
y(t) = \frac{d}{dt} x(t) ,
Suponga x1(t)= e(-t)u(t), semejante a lo usado en el ejercicio 1.
El desarrollo con el algoritmo muestra que el sistema resulta invariante en el tiempo.
-t -t
yf = e *DiracDelta(t) - e *Heaviside(t)
-t -t
yw = 2.71828182845905*e *DiracDelta(t - 1.0) - 2.71828182845905*e *Heaviside(t - 1.0)
-t -t
yf(t-t0) = 2.71828182845905*e *DiracDelta(t - 1.0) - 2.71828182845905*e *Heaviside(t - 1.0)
En este caso, dado que la señal de entrada tiene una función escalón, sympy no presenta inconvenientes en realizar la derivada. Sin embargo, la operacion de conversión con Lambdify será necesario añadir la equivalencia de DiracDelta en numpy. Por lo que la instrucción de Lambdify se le añade el parámetro para considerar los modulos equivalentes.
equivalentes = [{'DiracDelta': lambda x: 1*(x==0)},
'numpy']
Instrucciones en Python
Desarrollado a partir del algoritmo usado para sistemas lineales y no lineales
Ejemplo 1. Sistema con comportamiento senoidal
# entradas desplazadas en t, revisar salida # Revisa Invarianza en tiempo # Oppenheim 1.14 p51 pdf82 import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 1.0 # señales de entrada f = sym.exp(-t)*sym.Heaviside(t) w = f.subs(t,t-t0) # desplaza f # sistema y = sym.sin(x) # intervalo de t[a,b] para graficar a = 0 b = 2*np.pi muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() yf0 = yf.subs(t,t-t0).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf) ywt = sym.lambdify(t,yw) yf0t = sym.lambdify(t,yf0) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) yfi0 = yf0t(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) print('yf(t-t0):') sym.pprint(yf0) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistemas Invariante: y='+str(y)) plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.plot(ti,yfi0,'.',color='red', label='yft0=yf[t-t0]') plt.axhline(0) plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()
Ejemplo 2. Sistema comprime en tiempo
Para aplicar cambios en la variable tiempo, en el algoritmo se sustituye en la expresión de la señal de entrada la variable t por 2t.
# entradas desplazadas en t, revisar salida # Revisa Invarianza en tiempo # Oppenheim 1.16 p52.Hsu ejercicio 1.39 p48 import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 2.0 # señales de entrada f = sym.Heaviside(t+2)-sym.Heaviside(t-2) w = f.subs(t,t-t0) # desplaza f # sistema y = sym.Subs(x,t,2*t,evaluate=False) # intervalo de t[a,b] para graficar a = -5 b = 5 muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() yf0 = yf.subs(t,t-t0).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf) ywt = sym.lambdify(t,yw) yf0t = sym.lambdify(t,yf0) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) yfi0 = yf0t(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) print('yf(t-t0):') sym.pprint(yf0) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistemas Invariante: y='+str(y)) plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.plot(ti,yfi0,'--',color='red', label='yft0=yf[t-t0]') plt.axhline(0) plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()
Ejemplo 3. Sistema multiplica por tiempo
# entradas desplazadas en t, revisar salida # Revisa Invarianza en tiempo # Oppenheim 1.13 p49.Hsu ejercicio 1.38 p47 import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 2.0 # señales de entrada f = sym.sin(t) w = f.subs(t,t-t0) # desplaza f # sistema y = t*x # intervalo de t[a,b] para graficar a = 0 b = 3*np.pi muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() yf0 = yf.subs(t,t-t0).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf) ywt = sym.lambdify(t,yw) yf0t = sym.lambdify(t,yf0) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) yfi0 = yf0t(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) print('yf(t-t0):') sym.pprint(yf0) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistemas Invariante: y='+str(y)) plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.plot(ti,yfi0,'--',color='red', label='yft0=yf[t-t0]') plt.axhline(0) plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()
Ejemplo 4. Sistema deriva la entrada
# entradas desplazadas en t, revisar salida # Revisa Invarianza en tiempo # Lathi 1.11 p103 import numpy as np import sympy as sym import matplotlib.pyplot as plt equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, 'numpy'] # INGRESO t = sym.Symbol('t', real=True) x = sym.Symbol('x', real=True) t0 = 1.0 # señales de entrada f = sym.exp(-t)*sym.Heaviside(t) w = f.subs(t,t-t0) # desplaza f # sistema y = sym.diff(x,t,evaluate=False) # intervalo de t[a,b] para graficar a = 0 b = 2*np.pi muestras = 101 # PROCEDIMIENTO # Sistema sobre señal de entrada yf = y.subs(x,f).doit() yw = y.subs(x,w).doit() yf0 = yf.subs(t,t-t0).doit() # Para gráfica ti = np.linspace(a,b,muestras) # señales de entrada ft = sym.lambdify(t,f) wt = sym.lambdify(t,w) # señales de salida yft = sym.lambdify(t,yf,modules=equivalentes) ywt = sym.lambdify(t,yw,modules=equivalentes) yf0t = sym.lambdify(t,yf0,modules=equivalentes) # evalua entradas ti fi = ft(ti) wi = wt(ti) # evalua salidas ti yfi = yft(ti) ywi = ywt(ti) yfi0 = yf0t(ti) # SALIDA print('yf:') sym.pprint(yf) print('yw:') sym.pprint(yw) print('yf(t-t0):') sym.pprint(yf0) # grafica plt.subplot(211) # entradas plt.plot(ti,fi,'--', label='f(t)') plt.plot(ti,wi,'--',color='green', label='w(t)=f(t-t0)') plt.axhline(0) plt.xlabel('ti') plt.ylabel('entradas') plt.title('Sistemas Invariante: y='+str(y)) plt.legend() plt.grid() plt.subplot(212) # salidas plt.plot(ti,yfi,'--',label='yf=y[f(t)]') plt.plot(ti,ywi,'--',color='green', label='yw=y[w(t)]') plt.plot(ti,yfi0,'.',color='red', label='yft0=yf[t-t0]') plt.axhline(0) plt.xlabel('ti') plt.ylabel('salidas') plt.legend() plt.grid() plt.show()