1ra Evaluación II Término 2016-2017. 8/Diciembre/2016. TELG1001
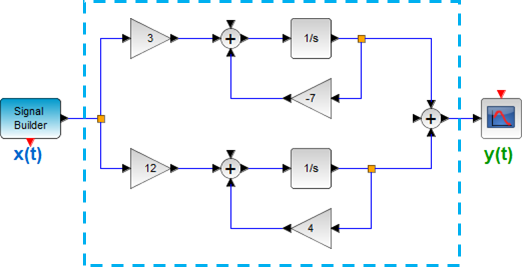
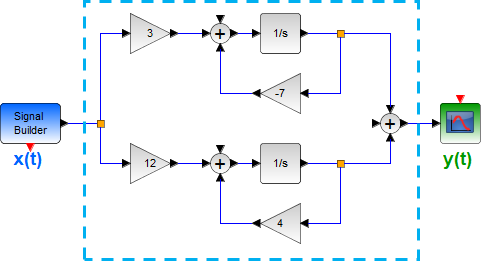
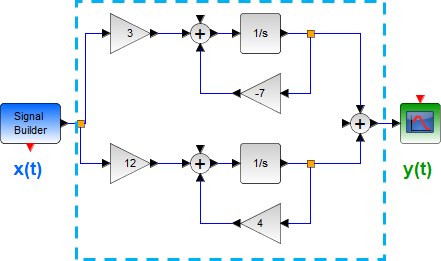
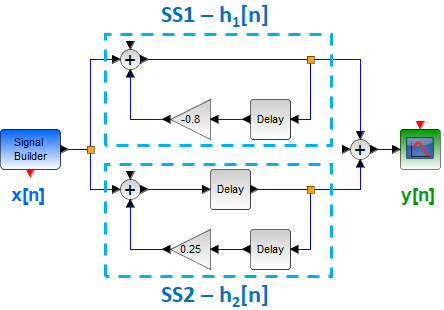
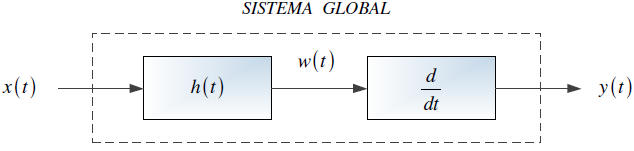
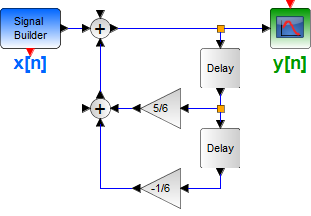
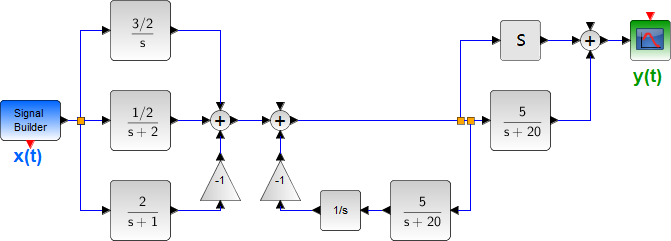
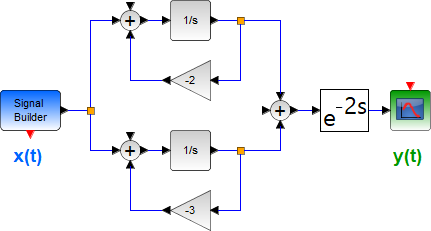
Tema 2. (16 puntos) Considere la existencia de un sistema LTI-CT, representado mediante diagrama de bloques en el dominio de la frecuencia compleja, relaciona la entrada-salida de la siguiente forma:
Adicionalmente se conoce que la Región de Convergencia de la funcion de transferencia del referido sistema es -7 < Re(s) < 4. Determinar:
a. La funcion de transferencia H(s) del mencionado sistema, esquematizando en el plano complejo su diagrama de polos y ceros.
b. La respuesta impulso h(t). Comente sobre la estabilidad, causalidad y memoria de éste sistema, justificando debidamente su respuesta.
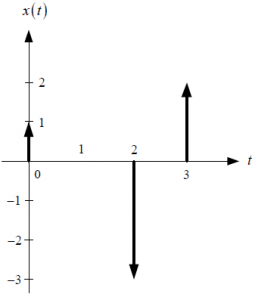
c. La respuesta de dicho sistema frente a la excitación
x(t) = e^{-5t} \mu (t)Referencia: 1Eva2012TII_T4 LTIC bloques en paralelo-serie con Laplace, 1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D
Coordinador: Tama Alberto