2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001
Tema 5. (20 puntos) Determinar la inversa de la transformada de Fourier de X(ω) cuya representación espectral se muestra a continuación.
2Eva2009TII_T4 LTI CT respuesta a x(t)
2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001
Tema 4. (20 puntos)
a. Determine las series de Fourier para la señal
x(t) = \cos (5t) \sin (3t)b. Esquematice el espectro de Fourier.
c. Dicha señal x(t) es aplicada a la entrada de un sistema LTI-CT cuya respuesta de frecuencia se muestra a continuación. Determine la salida de dicho sistema.
2Eva2009TII_T3 LTI CT modulador de frecuencia H(jω)
2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001
Tema 3. (20 puntos) Considere el sistema mostrado en la siguiente figura:
Donde:
x(t) = \frac{\sin (4\pi t)}{\pi t} p(t) = \cos (2\pi t) q(t) = \frac{\sin (2\pi t)}{\pi t}y la respuesta de frecuencia H(jω) está dada por:
Encontrar, esquematizar y etiquetar, según corresponda:
a. La transformada de Fourier de la señal a(t), es decir A(ω)
b. La transformada de Fourier de la señal b(t), es decir B(ω)
c. La respuesta del sistema c(t) sin esquematizar, ni etiquetar.
2Eva2009TII_T1 LTI CT subsistemas en serie con H(jω)
2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001
Tema 1. (20 puntos) Considere la existencia del siguiente sistema global que se muestra a continuación:
Se tiene conocimiento que
H_A (s) = \frac{10}{1+s}y que la aproximación en línea recta de los diagramas de Bode del Sistema Global H(jω) se muestran en las imágenes. Se solicita lo siguiente:
a. Determinar la función de transferencia HB(s)
b. Comentar brevemente, pero de manera justificada, sobre la estabilidad interna externa del Sistema Global.
c. Determinar la respuesta del Sistema Global frente a una excitación
x(t) = \cos (30t - 45^o)d. Obtener la realización DFII (forma canónica del Sistema Global.)
1Eva2016TII_T2 LTI CT bloques en paralelo-serie con Laplace
1ra Evaluación II Término 2016-2017. 8/Diciembre/2016. TELG1001
Tema 2. (16 puntos) Considere la existencia de un sistema LTI-CT, representado mediante diagrama de bloques en el dominio de la frecuencia compleja, relaciona la entrada-salida de la siguiente forma:
Adicionalmente se conoce que la Región de Convergencia de la funcion de transferencia del referido sistema es -7 < Re(s) < 4. Determinar:
a. La funcion de transferencia H(s) del mencionado sistema, esquematizando en el plano complejo su diagrama de polos y ceros.
b. La respuesta impulso h(t). Comente sobre la estabilidad, causalidad y memoria de éste sistema, justificando debidamente su respuesta.
c. La respuesta de dicho sistema frente a la excitación
x(t) = e^{-5t} \mu (t)Referencia: 1Eva2012TII_T4 LTIC bloques en paralelo-serie con Laplace, 1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D
Coordinador: Tama Alberto
1Eva2016TII_T1 LTI CT subsistema en paralelo-serie
1ra Evaluación II Término 2016-2017. 8/Diciembre/2016. TELG1001
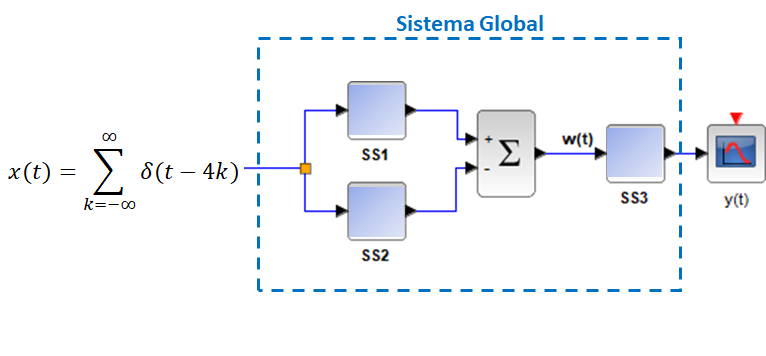
Tema 1. (28 puntos) Considere la existencia de un sistema global LTI-CT que ha sido integrado por la conexión en paralelo de dos subsistemas LTI-CT (SS1 y SS2). El sistema equivalente, es a su vez conectado en serie con otro subsistema LTI-CT (SS3).
«Respuestas de paso», y(t) ante una entrada escalón unitario x(t) = μ(t) se etiquetan como s(t)
El sistema global es excitado por x(t), conformado porun tren de impulsos unitarios, tal como se muestra en la figura. Conociendo las respuestas de paso de los subsistemas SS1, SS2 y SS3, se requiere lo siguiente:
a. Determinar las respuestas impulso de los subsistemas SS1, SS2 y SS3. es decir h1(t), h2(t), h3(t).
b. Determine la respuesta de paso (x(t) = μ(t)) del subsistema combinado SS12, es decir s12(t).
c. Determinar, esquematizar y etiquetar la respuesta impulso del sistema global, es decir h123(t). Encierre en un círculo la respuesta correcta en la tabla de éste enunciado.
| Sistema SS1 | Sistema SS2 | Equivalente SS1 y SS2 | Sistema SS3 | SISTEMA GLOBAL | ||||||
| CON MEMORIA | Si | No | Si | No | Si | No | Si | No | Si | No |
| CAUSAL | Si | No | Si | No | Si | No | Si | No | Si | No |
| BIBO ESTABLE | Si | No | Si | No | Si | No | Si | No | Si | No |
d. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del subsistema SS12, asi como su correspondiente potencia normalizada Pw(t).
d. Determinar, esquematizar y etiquetar la respuesta y(t) del precitado sistema global frente a la excitación x(t), asi como su correspondiente potencia normalizada Py(t).
Se debe presentar la justificación de su respuesta en las hojas de desarrollo. Tome en cuenta todas las consideraciones necesarias para presentar su respuesta.
Coordinador: Tama Alberto
1Eva2014TI_T3 LTI CT con subsistemas
1ra Evaluación I Término 2014-2015. 3/Julio/2014. TELG1001
Tema 3. (30 puntos) Considere la existencia del siguiente sistema global que se muestra en la figura:
Se tiene conocimiento que el esquema de bloques, en el dominio de tiempo, que relaciona la entrada-salida del Sistema A es el siguiente:
Adicionalmente, se conoce que un estudiante de la materia Sistemas Lineales, ha encontrado que la respuesta impulso hb(t) para el sistema B está definida por la siguiente relación:
h_b (t) = \delta '(t) - \delta (t) +8 e^{-5t} \mu (t)Determinar,
a. La ecuación diferencial de coeficientes constantes que relaciona la entrada-salida para ambos sistemas. Se pide que especifique las 2 ecuaciones diferenciales de coeficientes constantes.
b. La respuesta impulso del sistema global, es decir h(t)
c. La respuesta del sistema global frente a la entrada
x (t) = \sum_{k=-\infty}^{\infty} \delta (t-kT)Coordinador: Tama Alberto
1Eva2014TI_T1 LTI CT subsistemas en serie
1ra Evaluación I Término 2014-2015. 3/Julio/2014. TELG1001
Tema 1. (35 puntos) Para el sistema global, integrado por la conexión en serie de tres subsistemas:
Y, conociento la exitación x(t) y las respuestas de paso s(t) de los subsistemas SS1 y SS2.
Se le ha solicitado lo siguiente:
a. Determinar, esquematizar y etiquetar la respuesta impulso equivalente entre los subsistemas SS1 y SS2, es decir h12(t).
b. Determinar, esquematizar y etiquetar la respuesta impulso equivalente del sistema global, es decir h123(t).
c. Haciendo la debida justificación, encierre en un círculo, en la tabla que se muestra a continuación, la respuesta correcta.
d. Determinar, esquematizar y etiquetar la salida y(t).
e. Obtener el valor de la energía contenida en la señal de salida y(t)
| Sistema SS1 | Sistema SS2 | Equivalente SS1 y SS2 |
SISTEMA GLOBAL | |||||
| CON MEMORIA | Si | No | Si | No | Si | No | Si | No |
| CAUSAL | Si | No | Si | No | Si | No | Si | No |
| BIBO ESTABLE | Si | No | Si | No | Si | No | Si | No |
Coordinador: Tama Alberto
1Eva2012TII_T4 LTI CT bloques en paralelo-serie con Laplace
1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001
Tema 4. (25 puntos) Considere la existencia de un sistema LTI-CT cuya representación mediante diagrama de bloques en el dominio de la frecuencia compleja, que relaciona la entrada-salida del mismo, es la siguiente:
Adicionalmente, la Región de Convergencia de la función de transferencia del referido sistema es -7<Re(s)<4.
Determinar:
a. La función de transferencia H(s) del mencionado sistema y esquematizar su diagramas de polos y ceros en el plano complejo.
b. La respuesta impulso h(t). Comente sobre la estabilidad de éste sistema, justificando debidamente su respuesta.
c. La representación del mencionado sistema (en el dominio de tiempo contínuo) mediante diagrama de bloques.
d. La respuesta de dicho sistema frente a la entrada
x(t) = e^{-5t} \mu (t)Referencia: 1Eva2016TII_T2 LTIC bloques en paralelo-serie con Laplace, 1Eva2011TII_T3 LTI CT H(s) desde expresión con operadores D
Coordinador: Tama Alberto
1Eva2012TII_T3 LTI CT subsistemas en serie
1ra Evaluación II Término 2012-2013. 29/Noviembre/2012. TELG1001
Tema 2. (25 puntos) Para el sistema global integrado por la conexión en serie de tres subsistemas,
Y, conociendo la entrada o excitación x(t) junto con la respuesta de paso s(t) para el segundo subsistema, se le ha solicitado:
a. Determinar, esquematizar y etiquetar la respuesta w(t) que se genera a la salida del segundo subsistema LTI-CT, así como su correspondiente energía.
b. Indique justificadamente si el segundo subsistema es BIBO estable o no.
c. Mediante la aplicación de la propiedad de la derivación, obtener la transformada de Laplace de la señal w(t), esto es W(s).
d. Determinar, estquematizar y etiquetar la salida y(t)
e. Encontrar la relación entre las energías de la señal de salida y(t) a la señal de entrada x(t).