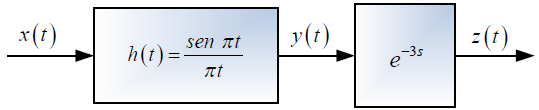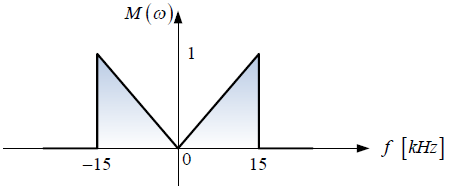Curso con Python – TELG1037/TELG1001 – FIEC – ESPOL
Tema 3. (25 puntos) Para la representación espectral que se muestra a continuación, determinar:
a. La inversa de la transformada de Fourier de X(ω), es decir x(t).
b. La energía contenida en la señal x(t)
Coordinador: Tama Alberto
Tema 3. (30 puntos) Para la representación espectral que se muestra a continuación, determinar:
a. La inversa de la transformada de Fourier de X(ω). Es decir x(t).
b. La energía contenida en la señal x(t).
Coordinador: Tama Alberto
Tema 1. (40 puntos) Un estudiante de la materia Sistemas Lineales ha encontrado que la respuesta impulso h(t), de un sistema LTI-CT, es aquella que se especifica en la siguiente figura.
Si el referido sistema es excitado con la señal cuadrada periódica x(t), determinar, esquematizar y etiquetar según corresponda, lo siguiente:
a. La respuesta de frecuencia H(ω) vs ω.
b. La respuesta de frecuencia X(ω) vs ω.
c. La respuesta de frecuencia Y(ω) vs ω y Z(ω) vs ω.
d. La expresión analítica de la salida y(t).
Coordinador: Tama Alberto
Tema 3. (20 puntos) Considere el sistema mostrado en la siguiente figura:
a. Determinar la frecuencia angular fundamental w0 y el periodo fundamental T0 de la señal v(t)
b. Esquematizar y etiquetar el espectro de las Series de Fourier de la señal v(t).
c. Determinr la potencia de la señal v(t).
d. Obtener la señal de respuesta y(t) de dicho sistema.
Coordinador: Tama Alberto
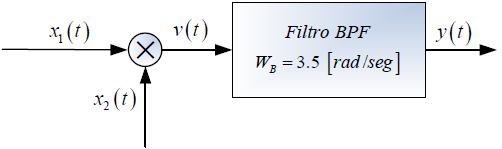
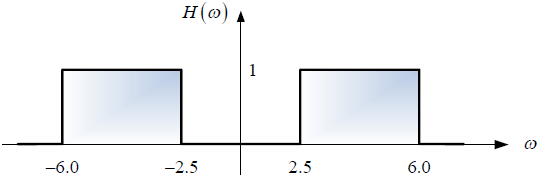
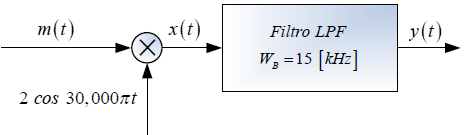
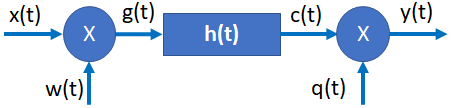
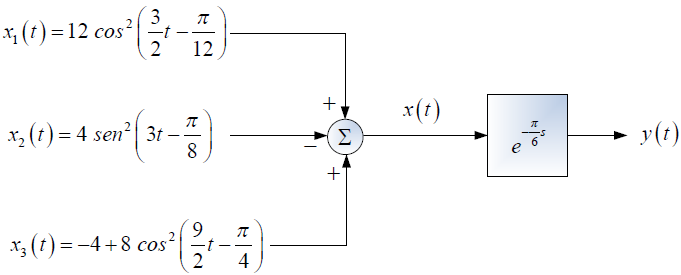
Tema 2. (40 puntos) Considere la existencia del sistema global que es producto de la conexión en cascada de dos subsistemas, tal como se muestra en la siguiente figura:
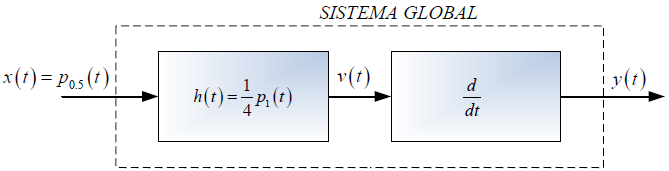
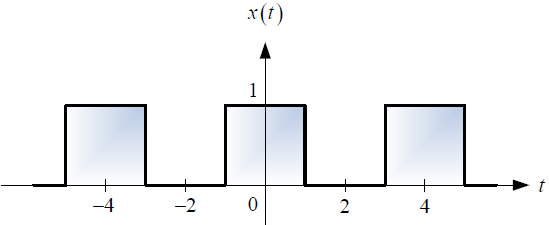
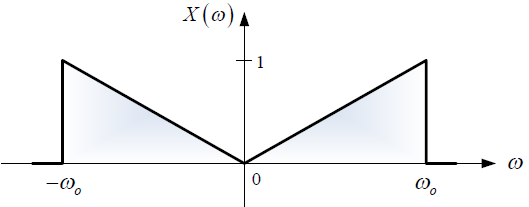
Un estudiante de la materia Sistemas Lineales, ha determinado que la forma de la señal de salida v(t) es aquella que se esquematiza a continuación.
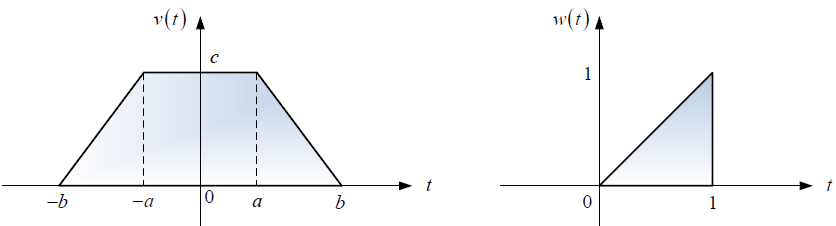
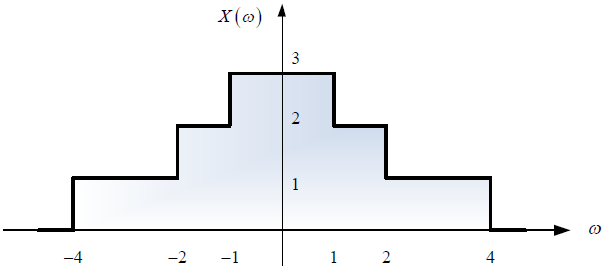
a. Obtener el valor que tomarían las constantes a, b, c.
b. Determinar la energía total contenida en la señal v(t).
c. Determinar, esquematizar y etiquetar la salida y(t) del sistema global y su energía total.
d. Dada la señal w(t), cuyo esquema se muestra anteriormente, expresar v(t) como una función de aquella.
e. Se conoce que la transformada de Fourier de la señal w(t) está dada por la siguiente expresión:
W(\omega) = \frac{1}{\omega^2} \Big( e^{j \omega} - j\omega e^{j\omega} -1 \Big)determine la transformada de Fourier de v(t).
Coordinador: Tama Alberto
Tema 1. (30 puntos) El sistema mostrado en la siguiente figura, es utilizado para distorsionar las señales de audio (scrambler-scrambling).
La señal x(t) es la versión modulada de la señal de entrada m(t), la misma que es la entrada a un filtro ideal pasa bajo, cuyo ancho de banda es de 15 [kHz]. De igual manera, también se puede afirmar que la salida del filtro pasa bajo y(t) es la versión distrorsionada de la señal de entrada m(t).
a. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal x(t); es decir X(ω) vs ω.
b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal y(t); es decir Y(ω) vs ω.
c. Utilizando la inversa de la Transformada de Fourier, determinar, esquematizar y etiquetar la señal de salida y(t).
Coordinador: Tama Alberto
Tema 4. (20 puntos) Para la representación espectral que se muestra a continuación, determinar:
a. La inversa de la transformada de Fourier de X(ω).
b. La energía contenida en la señal x(t).
Coordinador: Tama Alberto
Tema 2. (30 puntos) Considere el sistema LTI-CT, cuya respuesta al impulso unitario δ(t) es h(t), tal como se especifica en la siguiente figura.
Determinar, esquematizar y etiquetar según corresponda lo siguiente:
a. El espectro de Fourier de la señal g(t). Es decir G(ω) vs ω.
b. El espectro de Fourier de la respuesta impulso h(t). Es decir H(ω) vs ω.
c. El espectro de Fourier de la señal c(t). Es decir C(ω) vs ω.
d. El espectro de Fourier de la señal de salida y(t). Es decir Y(ω) vs ω.
Coordinador: Tama Alberto
Tema 4. (20 puntos) Determinar la inversa de la transformada de Fourier para X(ω), cuya representación espectral se muestra a continuación.
Coordinador: Tama Alberto
Tema3. (20 puntos) De acuerdo a la figura que se muestra a continuació, a un sistema LTI-CT cuya función de transferencia
H(s) = e^{\frac{\pi}{6}s}le ingresa una señal
x(t) = x1(t) – x2(t) + x3(t)
a. Determine y esquematice el espectro de magnitud y fase de las series de Fourier complejas y exponenciales de x(t).
b. Determine y esquematice el espectro de magnitud y fase de las series de Fourier complejas y exponenciales de y(t).
c. Determine la potencia de la señal de salida y(t).
Coordinador: Tama Alberto