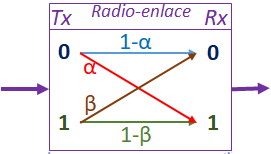
Ejercicio: 1Eva_IIT2017_T2 Radio-enlaces con Markov
Para un radio-enlace realice un modelo con una Cadena de Markov:
a) Determine el espacio de estados
s={0,1}
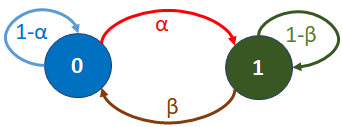
b) Realice el diagrama de estados, etiquete claramente
c) Escriba la matriz de transición y calcule la probabilidad de estado estable.
\begin{bmatrix} (1-\alpha) & \alpha\\ \beta & (1-\beta) \end{bmatrix}
(1-α) π0 + β π1 = π0
α π0 + (1-β) π1 = π1
π0 + π1 = 1
[(1-α)-1) π0 + β π1 = 0
α π0 + [(1-β)-1] π1 = 0
π0 + π1 = 1
Se seleccionan dos ecuaciones incluyento la suma de probabilidades es 1:
-α π0 + β π1 = 0 α π0 - β π1 = 0 π0 + π1 = 1
β π1 = α π0 π1 = α/β π0 π0 + α/β π0 = 1 (1 + α/β)π0 = 1 π0 = β/(β + α) π1 = α/(β + α)
Suponga que α=0.01, β=0.02 y determine para todo el enlace entre las ciudades:
d) La matriz de transición entre las ciudades A y B
p^{(3)}=\begin{bmatrix} 0.99 & 0.01\\ 0.02 & 0.98 \end{bmatrix}^{3}p = [[0.99, 0.01],
[0.02, 0.98]]
>>> p2 = np.linalg.matrix_power(p,2)
p2 = [[ 0.9803 0.0197]
[ 0.0394 0.9606]]
>>> p3 = np.linalg.matrix_power(p,3)
p3 = [[ 0.970891 0.029109]
[ 0.058218 0.941782]]
e) Probabilidad de error para un dígito binario 0 (bit)
P01 = 0.029109
f) Probabilidad de error para un bit con valor 1 (bit)
P10 = 0.058218
g) El error al transmitir un bit en todo el enlace
P01 + P10 = 0.029109 + 0.058218 = 0.0873
h) Observe y comente sus resultados
El sistema es semejante a usar una matriz de probabilidad para un sistema durante tres periodos de tiempo.
Las probabilidades se interpretan desde la matriz. Mientras más tramos se avanza en los radioenlaces, la probabilidad de falla aumenta, proporcional a los factores α y β.