2da Evaluación II Término 2017-2018. Febrero 7, 2018
Tema 1. Propuesta de solución
Y(x) = e^{-\alpha x}Siendo X de tipo uniforme entre (0,T]
f_x(x) = \frac{1}{T}Se puede calcular la función de densidad por cada punto de intersecciónal, al trazar una paralela al eje x que pasa por el punto y0
f_Y(y) = \sum_k \frac{f_x(x)}{|\frac{dy}{dx}|} \Big|_{x=x_0}De la gráfica del enunciado se encuentra que existe un solo punto de intersección (y0, x0).
Para un valor de y0 se encuentra su valor equivalente en x0,
y_0 = e^{-\alpha x_0} \ln (y_0) = \ln (e^{-\alpha x_0}) \ln (y_0) = -\alpha x_0 x_0 = \frac{\ln (y_0)}{-\alpha}la derivada dy/dx será
\frac{dy}{dx} = -\alpha e^{-\alpha x}Reemplazando en la ecuación para fY(y):
f_Y(y) = \frac{\frac{1}{T}}{|-\alpha e^{-\alpha x_0}|} = \frac{1}{T|-\alpha e^{-\alpha \frac{ln(y_0)}{-\alpha}}|} = \frac{1}{T|-\alpha e^{ln(y_0)}|} f_Y(y) = \frac{1}{T\alpha y}los valores de x se encuentran entre (0,T], por lo que los valores de y se encuentran:
y_0 = e^{-\alpha(0)} = 1 y_T = e^{-\alpha (T)} = e^{-\alpha T}el rango para y se encuentra entre 1 y e-αT.
La función de distribución acumulada:
F_Y(y) = \int_{1}^{y} f_Y(y) dy = \int \frac{1}{T\alpha y} dy = \frac{1}{T\alpha} \int \frac{1}{y} dy = \frac{1}{T\alpha} ln(y) \Big|_{1}^{y} = \frac{1}{T\alpha}(ln(y) - ln(1)) = \frac{1}{T\alpha}( ln(y) - 0) = \frac{1}{T\alpha}ln(y) F_Y(y) = \frac{ln(y)}{T\alpha}Gráfica: Para que la gráfica tenga una forma representativa, α=-1. 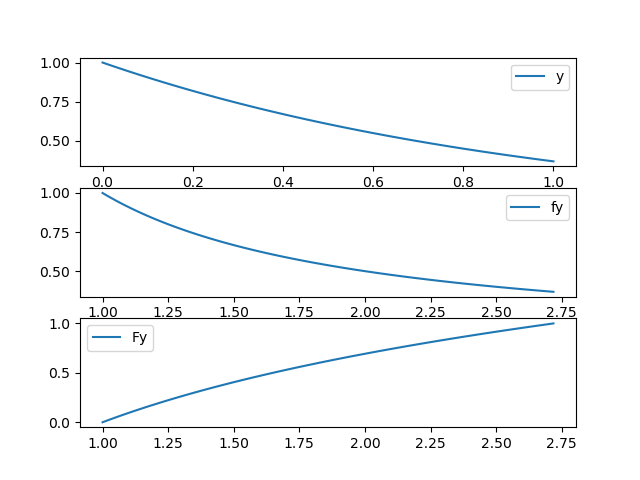
La auto-correlación aplica para funciones que dependen del tiempo, con diferencias de tiempo τ.
Para éste caso, no aplica la autocorrelación. tampoco se dispone de otra variable en el problema para realizar la correlación.
Script de python para presentar las gráficas del problema
import numpy as np import matplotlib.pyplot as plt # INGRESO alfa = -1 T = 1 # Rango de x a = 0 b = a + T # muestreo m = 100 # PROCEDIMIENTO funciony = lambda x: np.exp(alfa*x) pdf = lambda y: 1/(T*np.abs(alfa*y)) cdf = lambda y: np.log(y)/(np.abs(alfa)*T) x = np.linspace(a,b,m) yi = funciony(x) ya = funciony(alfa*a) yb = funciony(alfa*b) y = np.linspace(yb,ya,m) fy = pdf(y) Fy = cdf(y) # SALIDA plt.subplot(311) plt.plot(x, yi,label='y') plt.legend() plt.subplot(312) plt.plot(y,fy, label='fy') plt.legend() plt.subplot(313) plt.plot(y,Fy, label='Fy') plt.legend() plt.show()
