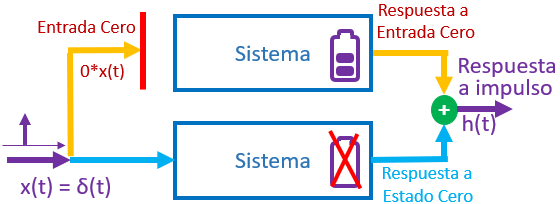
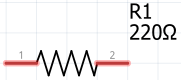
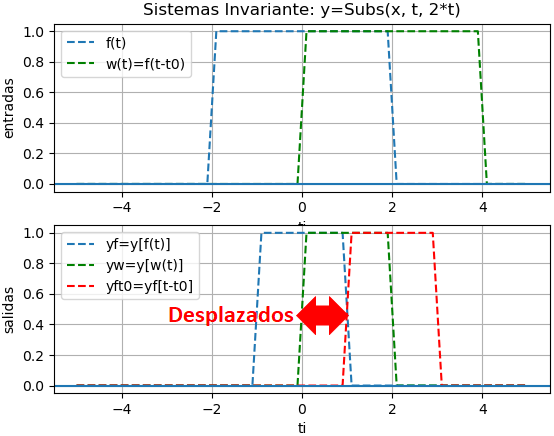
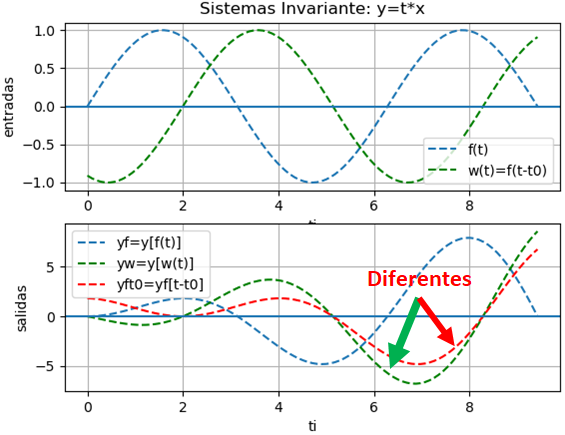
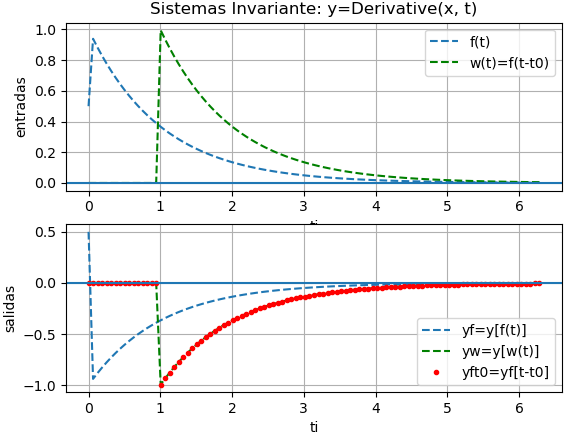
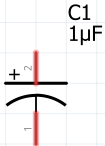La respuesta al impulso reutiliza el algoritmo de para encontrar la solución homogenea de la ecuación diferencial lineal. Se reutiliza la función respuesta_ZIR() de la sección anterior.
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]
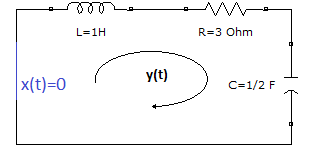
Ejemplo 1. Respuesta a impulso de un sistema RLC
Referencia: Lathi 1.8-1 p111. Ejercicio 2.1.a p 155. Oppenheim problema 2.61c p164, Ejemplo 9.24 p700.
Encontrar la Respuesta al impulso h(t), del sistema en el ejemplo 1 Modelo entrada-salida,
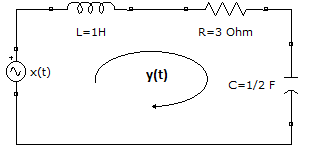representado por el circuito y la ecuación diferencial lineal expresada desde el termino de mayor orden:
La expresión en operadores D es:
(D^2 + 3D +2)y(t) = Dx(t)Siguiendo el método simplificado al emparejar impulsos, las condiciones iniciales, dado que el orden de las derivadas de la izquierda es 2, se establece como y'(0)=1, y(0)=0.
| N = 1 | yn(0) = 1 |
| N = 2 | yn(0) = 0, y’n(0) = 1 |
| N = 3 | yn(0) = 0, y’n(0) = 0, y"n(0) = 1 |
| N = 4 | … |
Siendo N el grado mayor de las derivadas de y(t) o lado izquierdo LHS y M el grado de mayor orden de las derivadas para x(t) o lado derecho RHS.
Si N>M, se tiene que b0=0. Si N=M el valor de b0 es el coeficiente de la derivada de mayor grado para x(t).
Desarrollo del algoritmo en Python
Se empieza buscando el orden N, para y(t) de las derivadas de la ecuación diferencial lineal. Con N se crea un vector ceros para condiciones de inicio y se escribe el valor de 1 a la primera casilla qu representa la posición de mayor orden de derivada .
# Método simplificado al emparejar impulsos N = sym.ode_order(ecuacion.lhs,y) M = sym.ode_order(ecuacion.rhs,x) # Condiciones iniciales para respuesta a impulso cond_inicio = [0]*N # lista de ceros tamano N cond_inicio[0] = 1 # condicion de mayor orden
Se debe buscar el coeficiente b0, que es el del término de mayor orden de la derivada para el lado derecho de la ecuación.
En la ecuacion parte derecha eq_RHS, se busca cada término hasta encontrar el de orden M. Se extrae el coeficiente del término encontrado. es decir todas las partes que no contienen el término de la derivada, ejemplo 3π.
# coeficiente de derivada de x(t) de mayor orden b0 = sym.nan if N>M: # orden de derivada diferente b0 = 0 if N==M: # busca coeficiente de orden mayor eq_RHS = sym.expand(ecuacion.rhs) term_suma = sym.Add.make_args(eq_RHS) for term_k in term_suma: # coeficiente derivada mayor if (M == sym.ode_order(term_k,x)): b0 = 1 # para separar coeficiente factor_mul = sym.Mul.make_args(term_k) for factor_k in factor_mul: if not(factor_k.has(sym.Derivative)): b0 = b0*factor_k
Con el valor de b0 y las cond_inicio se usa el algoritmo respuesta_ZIR() realizado para encontrar la respuesta a entrada cero a partir de la ecuación homogenea.
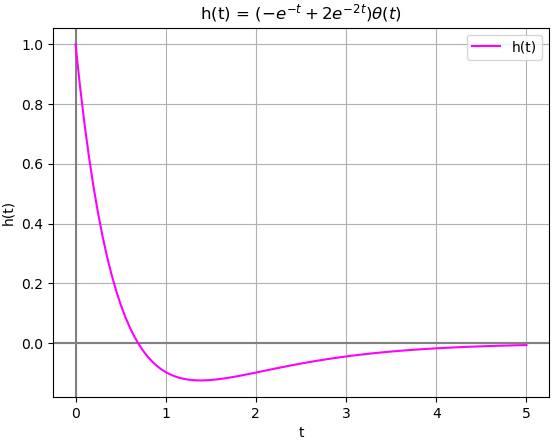
Con la ecuación homogenea y con las condiciones iniciales, y'(0)=1, y(0)=0, de una entrada impulso, se obtiene como respuesta:
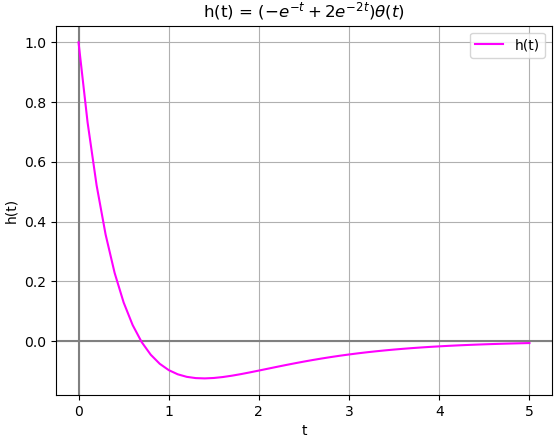
y(t) = C_1 e^{-t} + C_2 e^{-2t} y(t) = 1 e^{-t} -1 e^{-2t}A partir de la solución homogénea, se crea la función h(t) aplicando la expresión:
h(t)=b_0 \delta (t)+ [P(D)y_n (t)] \mu (t)y dado que para el ejercicio N>M, el orden de las derivadas de la izquierda es mayor que el orden de las derivadas de la derecha, se tiene que b0=0
h(t)=0 \delta (t) + [D y_n (t)] \mu (t)# ecuacion homogenea x(t)=0, entrada cero y # condiciones de impulso unitario sol_ht = fcnm.respuesta_ZIR(ecuacion,cond_inicio) # Respuesta a impulso h(t) P_y = ecuacion.rhs.subs(x(t),sol_ht['ZIR']).doit() h = P_y*u + b0*sym.DiracDelta(t) # h = sym.expand(h)
con lo que se llega a la respuesta de h(t),
h(t)= (-e^{-t} + 2e^{-2t})\mu (t)La respuesta del algoritmo en Python es:
clasifica EDO:
factorable
nth_linear_constant_coeff_variation_of_parameters
nth_linear_constant_coeff_variation_of_parameters_Integral
homogenea :
2
d d
2*y(t) + 3*--(y(t)) + ---(y(t)) = 0
dt 2
dt
general :
-t -2*t
y(t) = C1*e + C2*e
eq_condicion :
0 = C1 + C2
1 = -C1 - 2*C2
constante : {C1: 1, C2: -1}
ZIR :
-t -2*t
e - e
h :
/ -t -2*t\
\- e + 2*e /*Heaviside(t)
>>>
y con gráfica:
Instrucciones en Python
# Respuesta a impulso h(t) con Sympy-Python # http://blog.espol.edu.ec/telg1001/lti-ct-respuesta-al-impulso-con-sympy-python/ # Lathi 2.1.a pdf 155, (D^2+ 3D + 2)y = Dx import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') h = sym.Function('h') u = sym.Heaviside(t) d = sym.DiracDelta(t) # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 3*sym.diff(y(t),t,1) + 2*y(t) RHS = sym.diff(x(t),t,1,evaluate=False) ecuacion = sym.Eq(LHS,RHS) # cond_inicial con Método simplificado # de emparejar impulsos # Grafica: intervalo tiempo [t_a,t_b] t_a = 0 ; t_b = 5 muestras = 51 # PROCEDIMIENTO # Método simplificado al emparejar términos N = sym.ode_order(ecuacion,y) M = sym.ode_order(ecuacion,x) # coeficiente de derivada de x(t) de mayor orden b0 = sym.nan if N>M: # orden de derivada diferente b0 = 0 if N==M: # busca coeficiente de orden mayor eq_RHS = sym.expand(ecuacion.rhs) term_suma = sym.Add.make_args(eq_RHS) for term_k in term_suma: # coeficiente derivada mayor if (M == sym.ode_order(term_k,x)): b0 = 1 # para separar coeficiente factor_mul = sym.Mul.make_args(term_k) for factor_k in factor_mul: if not(factor_k.has(sym.Derivative)): b0 = b0*factor_k # Condiciones iniciales para respuesta a impulso cond_inicio = [0]*N # lista de ceros tamano N cond_inicio[0] = 1 # condicion de mayor orden # ecuacion homogenea x(t)=0, entrada cero y # condiciones de impulso unitario sol_yc = fcnm.respuesta_ZIR(ecuacion,cond_inicio) yc = sol_yc['ZIR'] # Respuesta a impulso h(t) P_y = ecuacion.rhs.subs(x(t),yc).doit() h = P_y*u + b0*d sol_yc['h'] = h edo_tipo = sym.classify_ode(ecuacion, y(t)) # SALIDA print('clasifica EDO:') for elemento in edo_tipo: print(' ',elemento) fcnm.print_resultado_dict(sol_yc) # GRAFICA ------------------ # Para graficar la Salida figura_h = fcnm.graficar_ft(h,t_a,t_b,muestras,'h') plt.show()
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]
Ejemplo 2. Ecuación diferencial lineal con Orden N=M
Referencia: Lathi. Ejercicio 2.4.a p167
Determine la respuesta al impulso de un sistema LTI C descrito por la siguiente ecuación diferencial ordinaria:
(D+2)y(t) = (3D+5) x(t)El orden N=M=1, por lo que aplican las condiciones iniciales de t0=0, y(0)=1, y'(0)=0 para resolver usando el algoritmo de respuesta a entrada cero para obtener y(t) y aplicar luego la expresión:
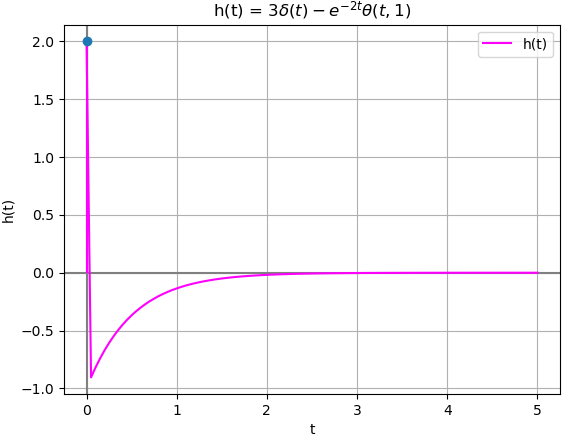
h(t)=b_0 \delta (t)+ [P(D)y_n (t)] \mu (t)siendo b0=3, que es el coeficiente de la derivada de mayor grado para el lado derecho de la expresión.
clasifica EDO:
1st_linear
almost_linear
nth_linear_constant_coeff_variation_of_parameters
1st_linear_Integral
almost_linear_Integral
nth_linear_constant_coeff_variation_of_parameters_Integral
homogenea :
d
2*y(t) + --(y(t)) = 0
dt
general :
-2*t
y(t) = C1*e
eq_condicion :
1 = C1
constante : {C1: 1}
ZIR :
-2*t
e
N : 1
M : 1
b0 : 3
h :
-2*t
3*DiracDelta(t) - e *Heaviside(t)
>>>
Instrucciones en Python
El ejercicio se desarrolla creando la función edo_resp_impulso() para ser incluida en telg1001.py y así simplificar el algoritmo para el próximo ejercicio.
# Respuesta a impulso h(t) con Sympy-Python # http://blog.espol.edu.ec/telg1001/lti-ct-respuesta-al-impulso-con-sympy-python/ # Lathi 2.1.a pdf 155, (D+2)y = (3D+5)x import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') h = sym.Function('h') u = sym.Heaviside(t) d = sym.DiracDelta(t) # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,1) + 2*y(t) RHS = 3*sym.diff(x(t),t,1,evaluate=False)+5*x(t) ecuacion = sym.Eq(LHS,RHS) # cond_inicial con Método simplificado # de emparejar impulsos # Grafica: intervalo tiempo [t_a,t_b] t_a = 0 ; t_b = 5 muestras = 51 # PROCEDIMIENTO def respuesta_impulso_h(ecuacion,t0=0, y = sym.Function('y'), x = sym.Function('x')): ''' respuesta a impulso h(t) de un sistema con Ecuacion Diferencial lineal ''' # Método simplificado al emparejar términos N = sym.ode_order(ecuacion,y) M = sym.ode_order(ecuacion,x) # coeficiente de derivada de x(t) de mayor orden b0 = sym.nan if N>M: # orden de derivada diferente b0 = 0 if N==M: # busca coeficiente de orden mayor eq_RHS = sym.expand(ecuacion.rhs) term_suma = sym.Add.make_args(eq_RHS) for term_k in term_suma: # coeficiente derivada mayor if (M == sym.ode_order(term_k,x)): b0 = 1 # para separar coeficiente factor_mul = sym.Mul.make_args(term_k) for factor_k in factor_mul: if not(factor_k.has(sym.Derivative)): b0 = b0*factor_k # Condiciones iniciales para respuesta a impulso cond_inicio = [0]*N # lista de ceros tamano N cond_inicio[0] = 1 # condicion de mayor orden # ecuacion homogenea x(t)=0, entrada cero y # condiciones de impulso unitario sol_yc = fcnm.respuesta_ZIR(ecuacion,cond_inicio) yc = sol_yc['ZIR'] # Respuesta a impulso h(t) P_y = ecuacion.rhs.subs(x(t),yc).doit() h = P_y*u + b0*d sol_yc['N'] = N sol_yc['M'] = M sol_yc['cond_inicio'] = cond_inicio sol_yc['b0'] = b0 sol_yc['h'] = h return(sol_yc) edo_tipo = sym.classify_ode(ecuacion, y(t)) # Respuesta a impulso h(t) sol_h = respuesta_impulso_h(ecuacion) h = sol_h['h'] # SALIDA print('clasifica EDO:') for elemento in edo_tipo: if 'linear' in elemento.split('_'): print(' ',elemento) fcnm.print_resultado_dict(sol_h) # GRAFICA ------------------ # Para graficar la Salida figura_h = fcnm.graficar_ft(h,t_a,t_b,muestras,'h') plt.show()
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]
Ejemplo 3. Ecuación diferencial lineal con Orden de N>M
Referencia: Lathi. Ejercicio 2.4.b p167
Determine la respuesta al impulso de un sistema LTI C descrito por la siguiente ecuación:
D(D+2)y(t) = (D+4) x(t)El orden N>M, por lo que aplican las condiciones iniciales de t0=0, y(0)=0, y'(0)=1 para resolver usando el algoritmo de respuesta a entrada cero para obtener y(t) y aplicar luego la expresión:
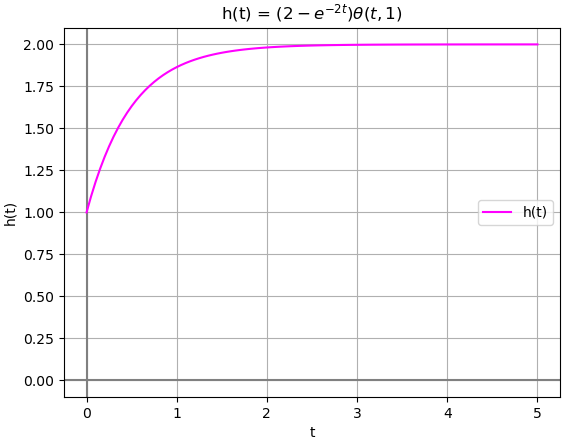
h(t)=b_0 \delta (t)+ [P(D)y_n (t)] \mu (t)siendo b0=0, que es el coeficiente de la derivada de mayor grado para el lado derecho de la expresión.
clasifica EDO:
nth_linear_constant_coeff_variation_of_parameters
nth_linear_constant_coeff_variation_of_parameters_Integral
homogenea :
2
d d
2*--(y(t)) + ---(y(t)) = 0
dt 2
dt
general :
-2*t
y(t) = C1 + C2*e
eq_condicion :
0 = C1 + C2
1 = -2*C2
constante : {C1: 1/2, C2: -1/2}
ZIR :
-2*t
1 e
- - -----
2 2
N : 2
M : 1
cond_inicio : [ 1 0 ]
b0 : 0
h :
/ -2*t\
\2 - e /*Heaviside(t)
>>>
Instrucciones en Python
# Respuesta a impulso h(t) con Sympy-Python # http://blog.espol.edu.ec/telg1001/lti-ct-respuesta-al-impulso-con-sympy-python/ # Lathi. Ejercicio 2.4.b p167 D(D+2)y(t) = (D+4)x(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t', real=True) y = sym.Function('y') x = sym.Function('x') h = sym.Function('h') u = sym.Heaviside(t) d = sym.DiracDelta(t) # ecuacion: lado izquierdo = lado derecho # Left Hand Side = Right Hand Side LHS = sym.diff(y(t),t,2) + 2*sym.diff(y(t),t,1) RHS = sym.diff(x(t),t,1,evaluate=False)+4*x(t) ecuacion = sym.Eq(LHS,RHS) # cond_inicial con Método simplificado de emparejar impulsos # Grafica: intervalo tiempo [t_a,t_b] t_a = 0 ; t_b = 5 muestras = 51 # PROCEDIMIENTO edo_tipo = sym.classify_ode(ecuacion, y(t)) # Respuesta a impulso h(t) sol_h = fcnm.respuesta_impulso_h(ecuacion) h = sol_h['h'] # SALIDA print('clasifica EDO:') for elemento in edo_tipo: if 'linear' in elemento.split('_'): print(' ',elemento) fcnm.print_resultado_dict(sol_h) # GRAFICA ------------------ figura_h = fcnm.graficar_ft(h,t_a,t_b,muestras,'h') plt.show()
Respuesta a Impulso: [Desarrollo Analítico] [Sympy-Python] [SciPy-Python] [Runge-Kutta] [Simulador]
