En los sistemas lineales, la causalidad se muestra con respuestas para t≥0, por lo que se usan términos multiplicados por escalón unitario μ(t). Mientras que la respuesta al impulso genera al menos un término con impulso unitario δ(t) con un coeficiente constante.
Para el desarrollo de los ejercicios, es de gran utilidad disponer de una función que permita buscar el impulso unitario dentro de una expresión de varios términos. Listar las ubicaciones de los impulsos es un resultado que se usa en la generación de gráficas, pues no siempre la muestra en el intervalo de tiempo usado se encuentra exactamente sobre la aplicación del impulso unitario.
Se propone usar dos funciones. una para encontrar dónde ocurre el impulso y otra para buscar donde y el sentido del escalón unitario.
1. Busca impulso unitario, DiracDelta(t) o δ(t) con Sympy
Si f(t) fuese solo δ(t), δ(t-1) o δ(t+1), el valor de desplazamiento de obtiene con el primer argumento de la función mediante ft.args[0] que al evaluarlo en cero y multiplicarlo por (-1) se tendría donde se aplica.
ecuacion = sym.Eq(ft.args[0],0) donde = sym.solve(ecuacion,t)
Para los casos como δ(-t-1), δ(-t+1) es necesario trabajar con el signo de la variable t. Una forma de evaluar la expresión interiores de los impulsos es obtener la ecuacion de la forma at+b=0 con sym.Eq(ft.args[0],0) y luego despejar el valor de t con la instrucción sym.solve(ecuacion,t).
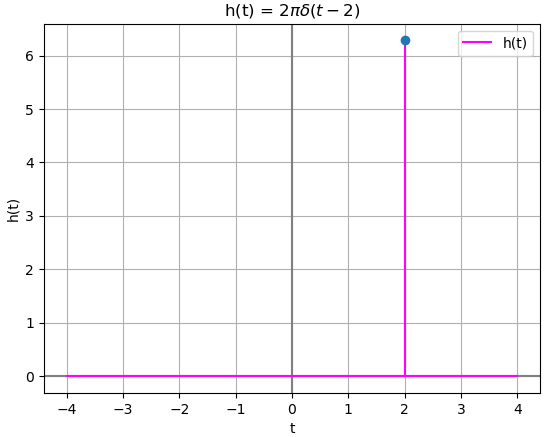
En expresiones simples de un solo término con coeficientes, se tiene:
h = 2*sym.pi*d.subs(t,t-2)
con resultados como:
h(t): 2*pi*DiracDelta(t - 2) busca_impulso(h): [2]
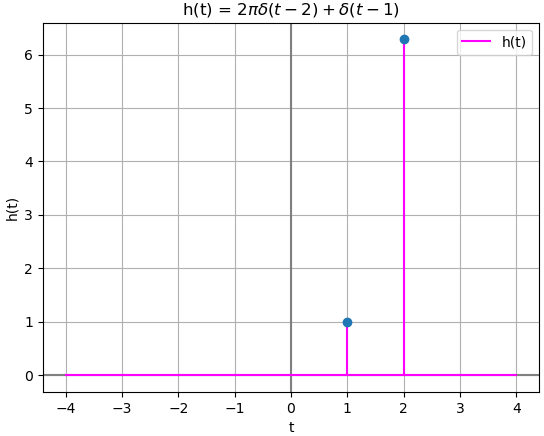
En el caso que se usen términos de varios impulsos, el valor de interés se encuentra usando el mínimo de la lista donde y observando que aún sea ≥0.
h = d.subs(t,t-1) + 2*sym.pi*d.subs(t,t-2)
con resuldado esperado de algoritmo
h(t): 2*pi*DiracDelta(t - 2) + DiracDelta(t - 1) busca_impulso(h): [1, 2]
Instrucciones en Python
# Busca impulso unitario en h(t) # http://blog.espol.edu.ec/telg1001/busca-impulso-unitario-o-escalon-unitario-con-sympy/ import sympy as sym import matplotlib.pyplot as plt import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) a = sym.Symbol('a',real=True) # busca impulso en h(t) # h = d # h = 2*sym.pi*d.subs(t,t-2) h = d.subs(t,t-1) + 2*sym.pi*d.subs(t,t-2) # h = 3*d.subs(t,t+1) # h = 5*sym.exp(-t)*d # h = 4 # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 51 # PROCEDIMIENTO def busca_impulso(ft): ''' busca en f(t) impulsos sym.DiracDelta entrega una lista ordenada de resultados ''' def impulso_donde(ft): ''' busca posicion de impulso en ft simple d, d**2 un solo termino,sin factores ''' ft = sym.sympify(ft,t) # convierte a sympy si es constante donde = [] # revisar f(t) sin impulsos if ft.has(sym.DiracDelta): if not(ft.is_Pow): # sin exponentes ecuacion = sym.Eq(ft.args[0],0) else: # con exponentes d**2 ecuacion = sym.Eq(ft.args[0].args[0],0) donde = sym.solve(ecuacion,t) return(donde) def impulso_donde_unterm(ft): ''' revisa impulso en un termino suma de ft ''' donde = [] # revisar f(t) sin impulsos factor_mul = sym.Mul.make_args(ft) for factor_k in factor_mul: if factor_k.has(sym.DiracDelta): donde_k = impulso_donde(factor_k) if len(donde) == 0: # vacio donde.extend(donde_k) if len(donde)>0: # sin repetir if not(donde_k[0] in donde): donde = [] # anulado por d(t-a)*d(t-b) return(donde) # revisa terminos suma ft = sym.sympify(ft,t) # convierte a sympy si es constante ft = sym.expand(ft) respuesta = [] term_suma = sym.Add.make_args(ft) for term_k in term_suma: donde = impulso_donde_unterm(term_k) if not(donde in respuesta) and len(donde)>0: respuesta.extend(donde) if len(respuesta)>1: # ordena ascendente respuesta.sort() respuesta = list(respuesta) return(respuesta) donde_d = busca_impulso(h) # SALIDA print('h(t):') sym.pprint(h) print('busca_impulso(h): ',donde_d) # Grafica figura_h = fcnm.graficar_ft(h,t_a,t_b,muestras,f_nombre='h') plt.show()
1. Busca escalón unitario, Heaviside(t) o μ(t) con Sympy
Para pruebas se tienen algunas expresiones de h(t), recordando que se analiza expresiones de un solo término, sin sumas o mutiplicaciones.
# entrada x(t) # h = u h = u.subs(t,t-1) # h = u.subs(t,t+1) # h = 5
Semejante al ejemplo anterior, se busca dónde se produce la transición del escalón unitario y el sentido si es de subida o de bajada como el signo de ‘t’.
\frac{d}{dt}\mu (t) = \delta(t)Con la función busca_impulso() obtiene donde se produce el impulso.
El sentido del escalón se obtiene al derivar la expresión del argumento. Si el escalón se desarrolla hacia de donde se produce, será positivo, y hacia la izquierda será negativo. Al aplicar escalon_donde(ft) permite determinar el punto de subida y bajada.
Para determinar el sentido del escalón unitario, se procede a tomar la expresion del argumento ft.args[0] y luego derivar con la instrucción sym.diff(ft.args[0]) para obtener el signo_t. con esto se observa si el desarrollo es hacia el lado derecho del plano (RHS). Con los parametros de donde y el sentido del escalón se puede aplicar un criterio de causalidad.
def escalon_donde(ft): ''' ft sin factores o terminos suma ''' ft = sym.sympify(ft,t) # convierte a sympy si es constante respuesta = [] if ft.has(sym.Heaviside): eq_u = sym.Eq(ft.args[0],0) sentido = sym.diff(eq_u.lhs,t,1) donde = sym.solve(eq_u,t)[0] respuesta = [donde,sentido] return(respuesta)
Instrucciones en Python
# Busca escalon unitario en h(t) # http://blog.espol.edu.ec/telg1001/busca-impulso-unitario-o-escalon-unitario-con-sympy/ import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) k = sym.Symbol('k',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada h(t) # h = u h = u.subs(t,t-1) # h = u.subs(t,t+1) # h = 5 # h = u + d # h = 3*sym.pi*u.subs(t,t-1)+ 2*d # h = sym.exp(-2*t)*u.subs(t,t+1) + sym.exp(-4*t)*u.subs(t,t-3) # h = sym.exp(-2*t)*sym.cos(t) + 4 # h = u.subs(t,-t+2)*u.subs(t,-t+1) # h = u.subs(t,-t+1)*u.subs(t,-t+1) # h = 3*u.subs(t,-t+1)*u.subs(t,-t+1) # h = u.subs(t,t-1)-u.subs(t,t-2) # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 51 # PROCEDIMIENTO def busca_escalon(ft): ''' busca en f(t) el donde,sentido de escalon unitario en un termino simple sin sumas, para ubicar lado del plano de f(t) ''' def escalon_donde(ft): ''' ft sin factores o terminos suma ''' ft = sym.sympify(ft,t) # convierte a sympy si es constante respuesta = [] if ft.has(sym.Heaviside): eq_u = sym.Eq(ft.args[0],0) sentido = sym.diff(eq_u.lhs,t,1) donde = sym.solve(eq_u,t)[0] respuesta = [donde,sentido] return(respuesta) def escalon_donde_unterm(ft): '''revisa termino de factores multiplica ''' respuesta = [] factor_mul = sym.Mul.make_args(ft) for factor_k in factor_mul: if factor_k.has(sym.Heaviside): ubicado = [] if not(factor_k.is_Pow): # sin exponente ubicado = escalon_donde(factor_k) else: # con exponentes d**k ubicado = escalon_donde(factor_k.args[0]) if len(ubicado)>0: respuesta.append(ubicado) return(respuesta) # revisa terminos suma ft = sym.sympify(ft,t) # convierte a sympy si es constante ft = sym.expand(ft) respuesta = [] term_suma = sym.Add.make_args(ft) for term_k in term_suma: donde = escalon_donde_unterm(term_k) if not(donde in respuesta) and len(donde)>0: respuesta.extend(donde) if len(respuesta)>1: # ordena ascendente respuesta = np.array(respuesta) columna = respuesta[:,0] ordena = np.argsort(columna) respuesta = respuesta[ordena] return(respuesta) donde_u = busca_escalon(h) # SALIDA print('h(t):') sym.pprint(h) print('busca_impulso:',fcnm.busca_impulso(h)) if len(donde_u)<=1: print('busca_escalon:',donde_u) else: print('busca_escalon:') print(busca_escalon(h)) # Grafica figura_h = fcnm.graficar_ft(h,t_a,t_b,f_nombre='h') plt.show()
Las funciones se las incorpora a los algoritmos telg1001.py
..