Categoría: 2da Evaluación

2da Evaluación II Término 2010-2011. 3/febrero/2011. TELG1001

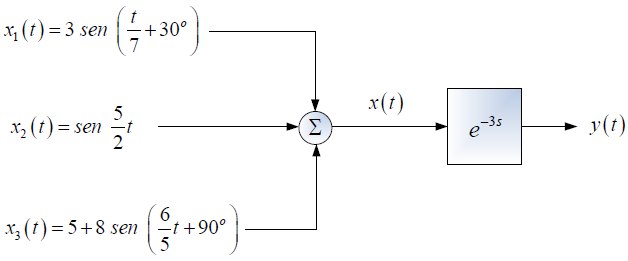
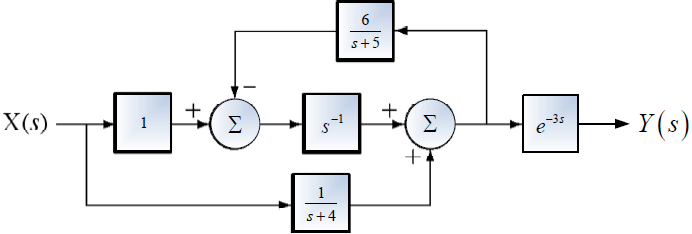
Tema 2. (35 puntos) Considere el sistema LTI-CT mostrado en la siguiente figura:

Donde:

x_1 (t) = \cos(2\pi t) x_2 (t) = \sin(6\pi t) h (t) = 2\frac{\sin (2\pi t)}{\pi t} \cos ( 7 \pi t)

Determinar, esquematizar y etiquetar segú corresponda:

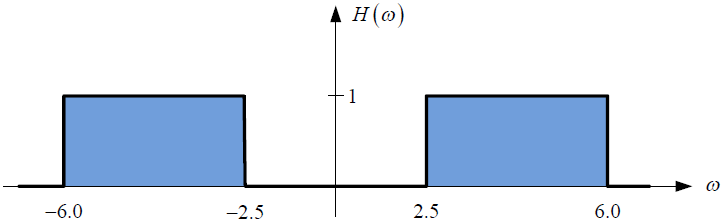
a. La transformada de Fourier h(t). Es decir H(ω) vs ω.

b. La transformada de Fourier de la señal y(t). Es decir Y(ω) vs ω.

c. La expresión analítica de la salida y(t) y su potencia.

d. Suponga ahora que se ingresa directamente a dicho sistema, un tren de impulsos descrito por:

x(t) = \sum_{k=-\infty}^{\infty} A \delta (t-kT_0)

con T₀=1.

Obtener la expresión analítica de la salida y(t) y su respectiva potencia.

---

Coordinador: Tama Alberto

2da Evaluación II Término 2010-2011. 3/febrero/2011. TELG1001

Tema 1. (35 puntos) Un estudiante de la materia Sistemas Lineales ha encontrado que la respuesta impulso h(t), de un sistema LTI-CT, es aquella que especifica en la siguiente figura.

Si el referido sistema es excitado con una señal rectangular periódica x(t), mostrada a continuación, determinar, esquematizar y etiquetar según corresponda, lo siguiente:

a. La respuesta de frecuencia H(ω) vs ω.

b. El espectro de amplitud y de fase de los coeficientes complejos de Fourier de la señal x(t), es decir D_k vs k y θ<subk vs k.

c. La expresión analítica de la salida y(t) y su potencia.

---

Coordinador: Tama Alberto

2da Evaluación I Término 2010-2011. 2/Septiembre/2010. TELG1001

Tema 4. (20 puntos) De ser posible, para el esquema mostrado en la siguiente figura, determinar, esquematizar y etiquetar según corresponda:

a. La representación espectral, (magnitud y fase) mediante Series de Fourier de la señal de entrada x(t).

b. La representación espectral (magnitud y fase) mediante Series de Fourier de la señal de salida y(t)

---

Coordinador: Tama Alberto

2da Evaluación I Término 2010-2011. 2/Septiembre/2010. TELG1001

Tema 2. (20 puntos) Considere el sistema mostrado en la siguiente figura:

Donde

w(t) = \cos(5 \pi t) h(t) = \frac{\sin (6 \pi t)}{\pi t}

y la respuesta de frecuencia de X(ω) esta dada por:

Encontrar, esquematizar y etiquetar, según corresponda:

a. La transformada de Fourier de la señal g(t). Es decir G(ω).

b. La transformada de Fourier de la señal c(t). Es decir C(ω).

c. La transformada de Fourier de la señal y(t). Es decir Y(ω).

---

Coordinador: Tama Alberto

2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001

Tema 5. (20 puntos) Determinar la inversa de la transformada de Fourier de X(ω) cuya representación espectral se muestra a continuación.

2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001

Tema 4. (20 puntos)

a. Determine las series de Fourier para la señal

x(t) = \cos (5t) \sin (3t)

b. Esquematice el espectro de Fourier.

c. Dicha señal x(t) es aplicada a la entrada de un sistema LTI-CT cuya respuesta de frecuencia se muestra a continuación. Determine la salida de dicho sistema.

2da Evaluación II Término 2009-2010. 4/Febrero/2010. TELG1001

Tema 3. (20 puntos) Considere el sistema mostrado en la siguiente figura:

Donde:

x(t) = \frac{\sin (4\pi t)}{\pi t} p(t) = \cos (2\pi t) q(t) = \frac{\sin (2\pi t)}{\pi t}

y la respuesta de frecuencia H(jω) está dada por:

Encontrar, esquematizar y etiquetar, según corresponda:

a. La transformada de Fourier de la señal a(t), es decir A(ω)

b. La transformada de Fourier de la señal b(t), es decir B(ω)

c. La respuesta del sistema c(t) sin esquematizar, ni etiquetar.