Referencia: Lathi 5.1 p488, Oppenheim 10.1 p741
Se define como X[z] a la transformada z de una señal x[n] como
X[z] = \sum_{n=-\infty}^{\infty} x[n] z^{-n}
Por razones semejantes a las descritas en la unidad 4 para transformadas de Laplace, es conveniente considerar la transformada z unilateral. Dado que muchos de los sistemas y señales son causales, en la práctica se considera que las señales inician en n=0 (señal causal), la definición de la transformada z unilateral es la misma que la bilateral. excepto por los limites de la sumatoria que son [0,∞]
X[z] = \sum_{n=0}^{\infty} x[n] z^{-n}
Ejemplo 1. Transformada z de exponencial causal
Referencia: Lathi ejemplo 5.1 p490, Oppenheim ejemplo 10.1 p743
Encuentre la Transformada z y la correspondiente ROC para la señal x[n]
x[n] = a ^{n} \mu[n]
![Transformada Z Ej01x[n]](http://blog.espol.edu.ec/telg1001/files/2017/07/TransformadaZ_Ej01xn.png)
1.1 Desarrollo analítico
por definición
X[z] = \sum_{n=0}^{\infty} a ^{n} \mu[n] z^{-n}
dado que μ[n]=1 para todo n≥0,
X[z] = \sum_{n=0}^{\infty} \Big( a^n \Big) \Big(\frac{1}{z} \Big)^{n} = \sum_{n=0}^{\infty} \Big(\frac{a}{z} \Big)^{n}
=1 + \Big(\frac{a}{z} \Big)^{1}+\Big(\frac{a}{z} \Big)^{2}+\Big(\frac{a}{z} \Big)^{3}+\text{...}
revisando la progresión geométrica,
1+x+x^2+x^3+\text{...} = \frac{1}{1+x} \text{ , }|x|<1
y aplicando en la expresión del problema, se tiene:
X[z] = \frac{1}{1-\frac{a}{z}}\text{ , } \Big|\frac{a}{z}\Big| <1
X[z] = \frac{z}{z-a}\text{ , } |z|>|a|
observe que X[z] existe solo si |z|>|a|. Para |z|<|a| la sumatoria no converge y tiende al infinito. Por lo que, la Región de Convergencia ROC de X[z] es la región sombreada de un círculo de radio |a| centrado en el origen en el plano z.
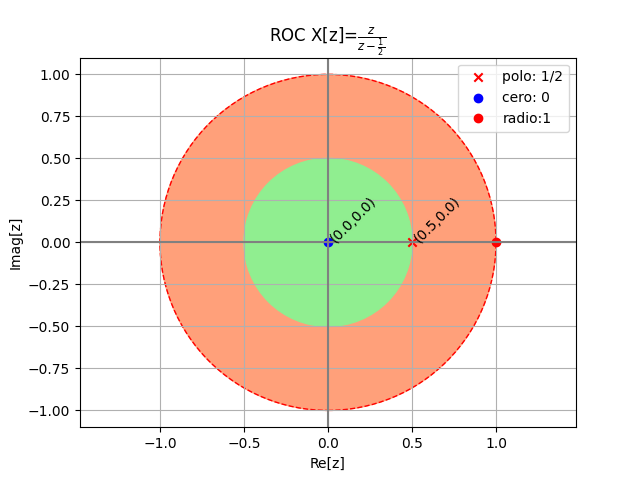
Luego se puede mostrar que la transformada z de la señal -an u[-(n+1)] también es z/(z-a). Sin embargo la región de convergencia en éste caso es |z|<|a|. Se observa que la transformada z inversa no es única, sin embargo,al restringir la transformada inversa a causal, entonces la transformada inversa es única como la mostrada.
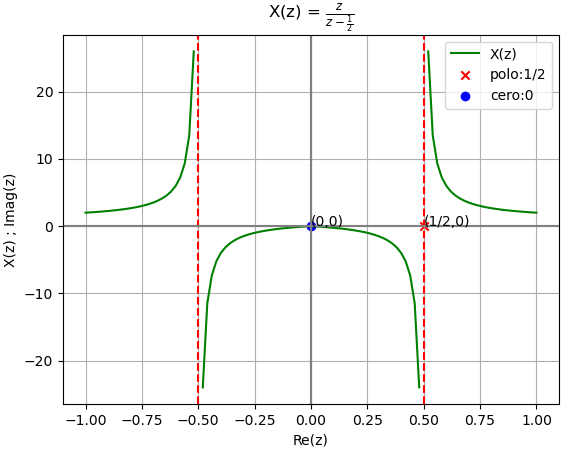
1.2 Transformada z con Sympy-Python
En Sympy de Python existe la función sym.summation(), que se usa para generar la expresión del resultado para la transformada z.
f[n]:
n
a
F[z] desde sumatoria:
1 |a|
(-------, |-| < 1)
a |z|
- - + 1
z
F[z] simplificada
z
------
-a + z
ROC:
|a|
|-| < 1
|z|
{Q_polos:veces}: {a: 1}
{P_ceros:veces}: {0: 1}
>>>
Instrucciones en Python
# transformada z de x[n]u[n]
import sympy as sym
# INGRESO
z = sym.symbols('z')
n = sym.symbols('n', positive=True)
a = sym.symbols('a')
u = sym.Heaviside(n)
fn = (a**n)*u
# valor a como racional en dominio 'ZZ' enteros
a_k = sym.Rational(1/2).limit_denominator(100)
m = 7 # Términos a graficar
muestras = 101 # dominio z
# PROCEDIMIENTO
fnz = fn*(z**(-n)) # f(n,z) para sumatoria
# sumatoria transformada z
Fz_sum = sym.summation(fnz,(n,0,sym.oo))
Fz_eq = Fz_sum.args[0] # primera ecuacion e intervalo
Fz = Fz_eq[0].simplify() # solo expresion
ROC = Fz_eq[1] # condicion ROC
# polos y ceros de Fz
[P,Q] = Fz.as_numer_denom()
P = sym.poly(P,z)
Q = sym.poly(Q,z)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)
# SALIDA
print('f[n]: ')
sym.pprint(fn)
print('\n F[z] desde sumatoria:')
sym.pprint(Fz_eq)
print('\n F[z] simplificada')
sym.pprint(Fz)
print('\n ROC: ')
sym.pprint(ROC)
print('\n {Q_polos:veces}:',Q_polos)
print(' {P_ceros:veces}:',P_ceros)
La parte gráfica se desarrolla reutilizando algunas funciones de los algoritmos telg1001.py
Ser requiere dar valor a la constante ‘a‘ y se sustituye en las funciones con a_k=1/2. Para actualizar los polos, se usa la función buscapolos() realizada en la unidad 4.3.2, añadiendo en la función la sustitución en F[z] de variable independiente a F(s) para que sea transparente el cálculo. Lo mismo se aplica a la grafica de la transformada F[z] y los resultados son los mostrados.
# GRAFICA -----------
import numpy as np
import matplotlib.pyplot as plt
import telg1001 as fcnm
def graficar_Fz_polos(Fz,Q_polos={},P_ceros={},
z_a=1,z_b=0,muestras=101,f_nombre='F',
solopolos=False):
''' polos y ceros plano z imaginario
'''
fig_zROC, graf_ROC = plt.subplots()
# limite con radio 1
radio1 = plt.Circle((0,0),1,color='lightsalmon',
fill=True)
radio2 = plt.Circle((0,0),1,linestyle='dashed',
color='red',fill=False)
graf_ROC.add_patch(radio1)
for unpolo in Q_polos.keys():
[r_real,r_imag] = unpolo.as_real_imag()
unpolo_radio = np.abs(unpolo)
unpolo_ROC = plt.Circle((0,0),unpolo_radio,
color='lightgreen',fill=True)
graf_ROC.add_patch(unpolo_ROC)
graf_ROC.add_patch(radio2) # borde r=1
graf_ROC.axis('equal')
# marcas de r=1 y polos
for unpolo in Q_polos.keys():
x_polo = sym.re(unpolo)
y_polo = sym.im(unpolo)
etiqueta = 'polo: '+str(unpolo)
graf_ROC.scatter(x_polo,y_polo,marker='x',
color='red',label = etiqueta)
etiqueta = "("+str(float(x_polo)) + ','
etiqueta = etiqueta + str(float(y_polo))+")"
plt.annotate(etiqueta,(x_polo,y_polo), rotation=45)
# marcas de ceros
for uncero in P_ceros.keys():
x_cero = sym.re(uncero)
y_cero = sym.im(uncero)
etiqueta = 'cero: '+str(uncero)
graf_ROC.scatter(x_cero,y_cero,marker='o',
color='blue',label = etiqueta)
etiqueta = "("+str(float(x_cero)) + ','
etiqueta = etiqueta + str(float(y_cero))+")"
plt.annotate(etiqueta,(x_cero,y_cero), rotation=45)
# limita radio 1
graf_ROC.plot(1,0,'o',color='red',
label ='radio:'+str(1))
graf_ROC.axhline(0,color='grey')
graf_ROC.axvline(0,color='grey')
graf_ROC.grid()
graf_ROC.legend()
graf_ROC.set_xlabel('Re[z]')
graf_ROC.set_ylabel('Imag[z]')
untitulo = r'ROC '+f_nombre+'[z]=$'
untitulo = untitulo+str(sym.latex(Fz))+'$'
graf_ROC.set_title(untitulo)
return(fig_zROC)
# a tiene valor a_k
fn = fn.subs(a,a_k)
Fz = Fz.subs(a,a_k)
# polos y ceros de Fz
polosceros = fcnm.busca_polosceros(Fz)
Q_polos = polosceros['Q_polos']
P_ceros = polosceros['P_ceros']
# estima intervalo para z
z_a = list(Q_polos.keys())
z_a.append(1) # comparar con radio 1
z_a = 2*int(max(z_a))
fig_ROC = graficar_Fz_polos(Fz,Q_polos,P_ceros,
muestras=101,f_nombre='X')
fig_Fz = fcnm.graficar_Fs(Fz,Q_polos,P_ceros,
-z_a,z_a,muestras=101,
f_nombre='X')
# para graficar f[n]
f_n = sym.lambdify(n,fn)
ki = np.arange(0,m,1)
fi = f_n(ki)
# entrada x[n]
fig_fn, grafxn = plt.subplots()
plt.axvline(0,color='grey')
plt.stem(ki,fi)
plt.grid()
plt.xlabel('n')
plt.ylabel('x[n]')
etiqueta = r'x[n]= $'+str(sym.latex(fn))+'$'
plt.title(etiqueta)
plt.show()
Referencia: The z-transform.dynamics-and-control. https://dynamics-and-control.readthedocs.io/en/latest/1_Dynamics/9_Sampled_systems/The%20z%20transform.html



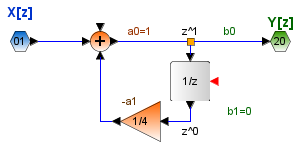
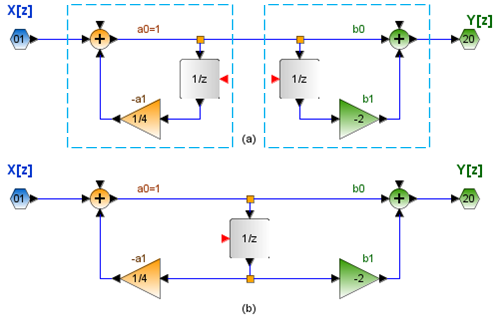
![Transformada Z Ej01 X[z] x[n]](http://blog.espol.edu.ec/telg1001/files/2017/07/TransformadaZ_Ej01Xz_Xn.png)
![Transformada Z Ej01x[n]](http://blog.espol.edu.ec/telg1001/files/2017/07/TransformadaZ_Ej01xn.png)

