Referencia: Lathi 5.4 p519. Oppenheim 10.8 p783, Hsu Ejercicio 4.34 p201
Dada la similitud entre sistemas LTIC y LTID, las convenciones para diagramas de bloques y las reglas de interconexión son idénticas a los sistemas contínuos. Los diagramas mostrados se realizan con el programa Xcos de SciLab.
Una función de transferencia general se expresa como:
H(z) = \frac{b_0 z^N +b_1 z^{N-1} + \text{ ... } + b_{N-1} z + b_N}{z^N + a_1 z^{N-1} +\text{ ... } + a_{N-1}z +a_N}Ejemplo 1. H(z)
Referencia : Lathi 5.8a p522
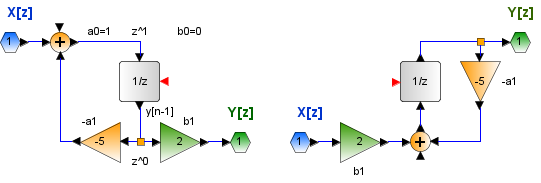
H(z) =\frac{2}{z+5}La función de transferencia es de primer orden (N=1), por lo que solo se usará un retraso para el diagrama. Los coeficientes de retroalimentación de retraso y adelanto son:
a1= 5 y b0 = 0, b1=2
La imagen presenta dos formas de realizar los diagramas
Ejemplo 2. H(z)
Referencia : Lathi 5.8b p522
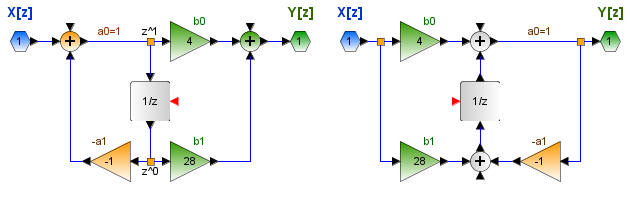
H(z) =\frac{4z+28}{z+1}la función de transferencia también es de primer orden (N=1), los coeficientes de retraso y adelanto son:
a1= 1 y b0 = 4, b1=28
La imagen presenta dos formas de realizar el diagrama de bloques
Ejemplo 3. H(z)
Referencia : Lathi 5.8c p522
H(z) =\frac{z}{z+7}la función de transferencia también es de primer orden (N=1), los coeficientes de retraso y adelanto son:
a1= 7 y b0 = 1, b1=0
Ejemplo 4. H(z)
Referencia : Lathi 5.8d p522
H(z) =\frac{4z+28}{z^2+6z+5}la función de transferencia también es de segundo orden (N=2), los coeficientes de retraso y adelanto son:
a1= 6, a2= 5 y b0 = 0, b1=4, b2=28
Ejemplo 5. Sistema LTI D
Referencia: Ejemplo Openheim 10.28 p784
Considere el sistema LTI causal descrito mediante:
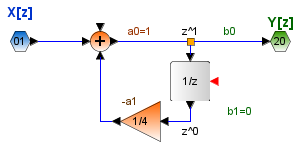
y[n] - \frac{1}{4} y[n-1] = x[n]con función del sistema:
H(z) =\frac{1}{1- \frac{1}{4} z^{-1} }Aqui z-1 es la función del sistema con retraso unitario. El diagrama de bloques en la figura contiene un lazo de retroalimentación.
y[n] -\frac{1}{4} z^{-1} y[n] = x[n] y[n] = x[n] + \frac{1}{4} z^{-1} y[n]Ejemplo 6. Función H(z)
Referencia: Ejemplo Openheim 10.29 p785
Considere un sistema LTI causal con función del sistema:
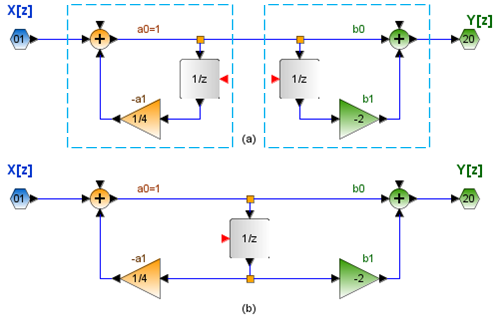
H(z) = \frac{ 1 - 2 z^{-1} }{ 1 - \frac{1}{4} z^{-1} }La función se puede separar en bloque de denominador y numerador, semejante a los polinomios Q(E) y P(E).
= \Bigg[\frac{1}{1 - \frac{1}{4}z^{-1}} \Bigg] \Bigg[ 1 - 2z^{-1} \Bigg]Se observa en el diagrama (a) que z-1 se encuentra duplicado pues ambos bloques toman la misma señal para aplicarle un atraso, cada uno le da a una ganancia diferente. Por lo que un solo bloque z-1 puede realizar la misma operación.
En el mundo de los circuito digitales y componentes, la situación se interpreta como un componente duplicado, lo que tiene implicaciones de costos de implementación, recuerde el tema cuando construye un circuito digital usando puertas lógicas y registros.