La transformada z convierte las ecuaciones de diferencias en expresiones algebraicas que permiten encontrar soluciones en el dominio z. A partir de las soluciones en el dominio z, se aplica la transformada inversa z que lleva a la solución en el dominio del tiempo
Ejercicio1
Referencia: Lathi Ejemplo 5.5 p510
Resolver
y[n+2] – 5 y[n+1] + 6 y[n] = 3 x[n+1] + 5 x[n]
con las condiciones iniciales y[-1]=11/16, y[-2]=37/36,
ante una entrada x[n]=(2)-nμ[n]
Desarrollo analítico
Usando la propiedad de desplazamiento de 2 unidades a la derecha.
y[n] – 5 y[n-1] +6 y[n-2] = 3 x[n-1] + 5 x[n-2]
se aplica la transformada z, teniendo en cuenta que y[n-k] significa y[n-k]μ[n], pues consideramos solamente la situación de n≥0, y[n] esta presente incluso antes de n=0.
Teniendo así que,
y[n] μ[n] \Leftrightarrow Y[z] y[n-1] μ[n] \Leftrightarrow \frac{1}{z} Y[z] + y[-1] = \frac{1}{z} Y[z] + \frac{11}{6} y[n-1] μ[n] \Leftrightarrow \frac{1}{z} Y[z] + \frac{11}{6} y[n-2] μ[n] \Leftrightarrow \frac{1}{z^2} Y[z] + \frac{1}{z}y[-1] + y[-2] y[n-2] \mu [n] \Leftrightarrow \frac{1}{z^2} Y[z] + \frac{1}{z}\frac{11}{6} +\frac{37}{36}Conociendo que para una entrada causal x[n]
x[-1] = x[-2] = … = x[-n] = 0
se tiene que:
x[n] = (2)^{-n} \mu [n] = (2^{-1})^n \mu [n] = (0.5)^n \mu [n] \Leftrightarrow \frac{z}{z-0.5} x[n-1] \mu [n] \Leftrightarrow \frac{1}{z}X[z] +x[-1] = \frac{1}{z}\frac{z}{z-0.5} +0= \frac{1}{z-0.5} x[n-2] \mu [n] \Leftrightarrow \frac{1}{z^2}X[z] + \frac{1}{z}x[-1] + x[-2] = = \frac{1}{z^2} \frac{z}{z-0.5} + (0) + (0) = \frac{1}{z(z-0.5)}en general, para una entrada causal:
x[n-r] \mu [n] \Leftrightarrow \frac{1}{z^r}X[z]tomando los resultados anteriores y reemplazado en la ecuacion inicial, de tiene
Y[z] - 5 \Bigg[ \frac{1}{z} Y[z] + \frac{11}{6}\Bigg] + 6 \Bigg[\frac{1}{z^2} Y[z] + \frac{1}{z}\frac{11}{6} +\frac{37}{36} \Bigg] = = 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}reagrupando términos Y[z] y reordenando,
\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] +\Bigg(-5\frac{11}{6}+ \frac{1}{z}\frac{11}{6}6 +6\frac{37}{36} \Bigg) = = 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)} \Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] + \Bigg(-3 + \frac{11}{z} \Bigg) = 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)} \Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = -\Bigg(-3 + \frac{11}{z} \Bigg) + 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)}En el lado derecho se muestran términos generados por una respuesta natural y una respuesta forzada. Dicho de otra forma, se muestran términos generados por las condiciones iniciales y por la señal x[n].
reagrupando el lado derecho en forma de numerador y denominador
\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = \frac{3z^2 -9.5z +10.5}{z(z-0.5)}se puede reescribir, multiplicando cada lado por z2
z^2\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = z^2 \Bigg[\frac{3z^2 -9.5z +10.5}{z(z-0.5)} \Bigg] (z^2 - 5 z + 6) Y[z] = \frac{z(3z^2 -9.5z +10.5)}{(z-0.5)} Y[z] = \frac{z(3z^2 -9.5z +10.5)}{(z-0.5)(z^2 - 5 z + 6)}se aplica fracciones parciales, usando el algoritmo de la sección Transformada z-fracciones parciales
Y[z] = \frac{26}{15}\frac{z}{z-0.5} - \frac{7}{3}\frac{z}{z-2} + \frac{18}{5}\frac{z}{z-3}usando la tabla de transformadas z, se obtiene como respuesta en el tiempo discreto
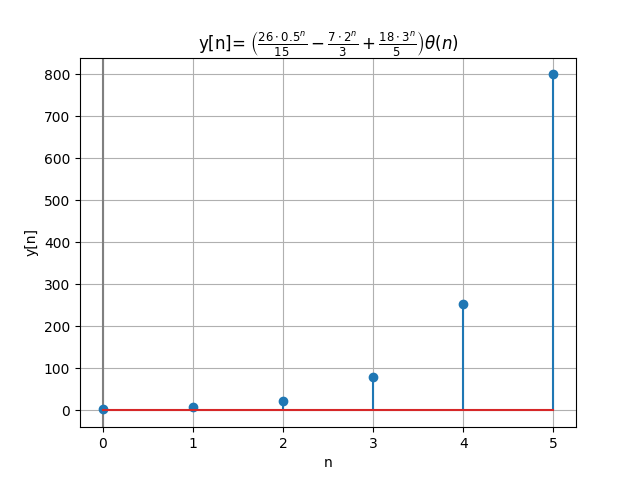
y[n] = \Bigg[ \frac{26}{15}(0.5)^n - \frac{7}{3}(2)^n + \frac{18}{5}(3)^n \Bigg] \mu [n]