Referencia: Lathi Ej 2.8 p173.
La función h(t) o respuesta al impulso se compone de un término de impulso y un escalón que multiplica a los modos característicos de la ecuación diferencial.
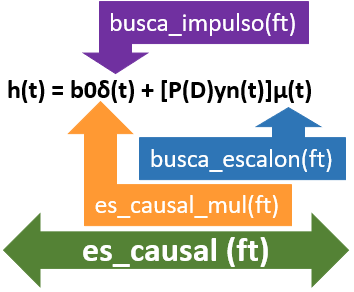
h(t)=b_0 \delta (t)+ [P(D)y_n (t)] \mu (t)La comprobación de causalidad considera tomar como referencia la búsqueda de un δ(t) o un μ(t) del lado derecho del plano, t≥0. Se considera que el sistema responde solo cuando le llega una señal a partir de t≥0, por lo que los componentes de h(t) deben encontrarse en el lado derecho del plano.
La causalidad de h(t) se usa para determinar los límites del integral de convolución que facilitan las operaciones para obtenerlo. El algoritmo de comprobación de causalidad se compone de las partes para analizar la expresión de h(t) descritas en la imagen.
Se propone desarrollar algunos ejercicios de forma progresiva, empezando de lo pequeño hacia lo grande.
Para generalizar el algoritmo, en adelante h(t) se denominará f(t).
..
Ejemplo 1. busca el punto t donde se produce el impulso δ(t)
Referencia: h(t) de Lathi Ej. 2.13 p200
El primer objetivo es determinar si tan solo un término simple contiene un impulso δ(t), no existen otros terminos sumados. El ´término puede estar desplazado o multiplicado por otros factores.
# entrada x(t) # h = d h = 2*sym.pi*d.subs(t,t-2) # h = 2*d.subs(t,t-1) # h = 3*d.subs(t,t+1) # h = 5*sym.exp(-t)*d
La instrucción para revisar que aún no existan de términos de suma es not(ft.is_Add).
Si f(t) tiene un impulso se puede revisar con ft.has(sym.DiracDelta), que inicialmente sería suficiente para los objetivos del ejercicio. Sin embargo en ejercicios posteriores y de evaluación se encontrará que estas funciones se pueden desplazar hacia un lado del plano, tal como un retraso en el tiempo de procesamiento. Por lo que se considera necesario determinar el punto t donde se aplica el impulso y observar si es en el lado derecho del plano, t≥0.
La función a usar se desarrollada para buscar impulsos unitarios en una expresión es:
donde_d = fcnm.busca_impulso(h)
En el caso de disponer de varios valores, es de interés el valor que se encuentre más hacia la izquierda, es decir los valores encontrados deben ser ordenados previamente. Si los impulsos ocupan solamente el lado derecho del plano, el sistema es causal.
donde_d = fcnm.busca_impulso(h) # Causal en RHS hcausal = False if len(donde_d)>0: donde=donde_d[0] # extremo izquierdo if donde>=0: # lado derecho del plano hcausal=True
Para el siguiente ejemplo se debería obtener:
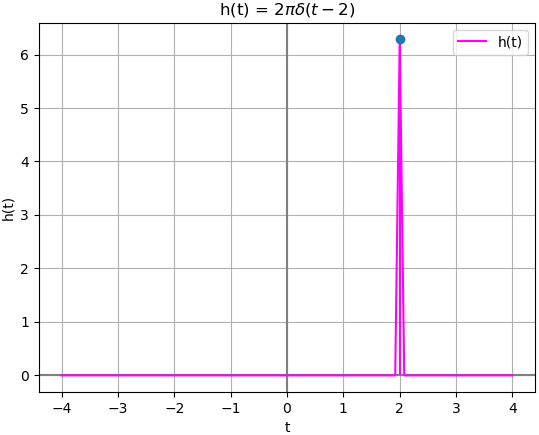
h(t): 2*pi*DiracDelta(t - 2) hcausal: True
con gráfica mostrando la causalidad de h(t) como un retraso de la entrada.
Instrucciones en Python
# Revisar causalidad de ft(t) en sympy # considera causal h(t)=b0*d + (modos caracteristicos)*u # Parte 1 comprueba solo impulso d(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t) # h = d h = 2*sym.pi*d.subs(t,t-2) # h = d.subs(t,t-1) # h = 3*d.subs(t,t+1) # h = 5*sym.exp(-t)*d # h = 4 # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 51 # PROCEDIMIENTO donde_d = fcnm.busca_impulso(h) # Causal en RHS hcausal = False if len(donde_d)>0: donde=donde_d[0] # extremo izquierdo if donde>=0: # lado derecho del plano hcausal=True # SALIDA print('h(t):') sym.pprint(h) print('hcausal: ',hcausal) # Grafica figura_h = fcnm.graficar_ft(h,t_a,t_b,f_nombre='h') plt.show()
Ejemplo 2. f(t) es causal si contiene escalón unitario μ(t) en un termino simple, sin sumas, N>M
Referencia: Lathi 2.6-3 p206, Ej.2.13 p188
Ahora considere un termino de los modos característicos multiplicado por un escalón unitario μ(t) según el modelo de respuesta a impulso h(t).
h(t)=0 \delta (t)+ [P(D)y_n (t)] \mu (t)la causalidad del escalón require primero encontrar desde dónde se aplican y luego la dirección o sentido. De forma semejante a la búsqueda de impulsos, se crea una función que busque el escalón e indique [donde, sentido]
Para un escalón unitario hacia la derecha se tiene como punto de partida que causal=False, cambiando a True en el caso que el impulso se encuentre a la derecha del plano y el sentido sea positivo.
causal = False h = fcnm.simplifica_escalon(h) # h(t-a)*h(t-b) if h.has(sym.Heaviside): #sin factores donde_u = busca_escalon(h) if len(donde_u)>0: donde = donde_u[0][0] sentido = donde_u[0][1] if donde>=0 and sentido>0: causal = True
El resultado esperado del algoritmo, para un caso es:
h(t): Heaviside(t - 1) busca_impulso: [] busca_escalon(ft): [[1, 1]] xcausal: True
en la gráfica se observa el desarrollo hacia el lado derecho,
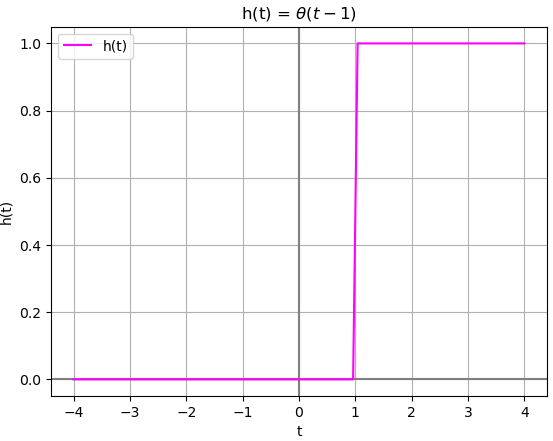debiendo realizar otras pruebas para verificar o mejorar el algoritmo.
# Revisar causalidad de ft(t) en sympy # considera causal h(t)=b0*d + (modos caracteristicos)*u # Parte 1 comprueba solo impulso d(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) k = sym.Symbol('k',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t) # h = u h = u.subs(t,t-1) # h = u.subs(t,t+1) # h = 5 # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 51 # PROCEDIMIENTO donde_u = fcnm.busca_escalon(h) # Causal en RHS causal = False if len(donde_u)>0: # existe un escalon unitario donde = donde_u[0][0] sentido = donde_u[0][1] if donde>=0 and sentido>0: # lado derecho del plano causal = True # SALIDA print('h(t):') sym.pprint(h) print('busca_impulso:', fcnm.busca_impulso(h)) print('busca_escalon(ft):', donde_u) print('xcausal: ',causal) # Grafica figura_h = fcnm.graficar_ft(h,t_a,t_b,f_nombre='h') plt.show()
Ejemplo 3. Revisa si f(t) es causal un término de factores que se multiplican
Referencia: h(t) de Lathi Ej. 2.10 p181
Se amplia el algoritmo anterior para incorporar la revisión de f(t) con factores que se multiplican.
Se muestras algunos ejemplos a usar para analizar esta parte:
# entrada x(t) # h = u # h = 3*sym.pi*u.subs(t,t-1) h = sym.exp(-2*t)*u.subs(t,t+1) # h = sym.exp(-2*t)*sym.cos(t) # h = 5 # h = u.subs(t,-t+2)*u.subs(t,-t+1) # h = u.subs(t,-t+1)*u.subs(t,-t+1) # h = 3*u.subs(t,-t+1)*u.subs(t,-t+1) # h = u.subs(t,t+1)*u.subs(t,-t+1) # h = u.subs(t,t-1)*u.subs(t,-t+2) # h = u.subs(t,t+2)*u.subs(t,-t-1) # h = u.subs(t,t-2)*u.subs(t,-t-1)
El resultado esperado del algoritmo para uno de los ejemplos presentados en la entrada del algoritmo es:
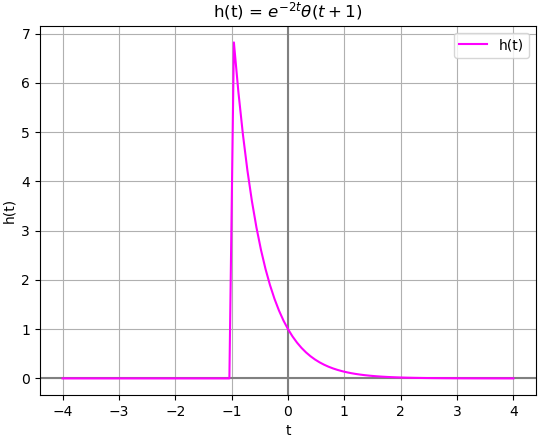
h(t): -2*t e *Heaviside(t + 1) hcausal: False
El resultado indica que no es causal, que es concordante con la gráfica pues este sistema tiene respuesta antes de t=0, en el lado izquierdo del plano. Es decir el sistema se ‘adelanta’ a la llegada de la señal en el tiempo.
La revisión de factores de cada término de suma, se realiza descomponiendo la expresión en sus factores con ft.args o se obtienen los término suma con term_suma = sym.Add.make_args(ft)
En el caso que el termino sea un escalon o impulso elevado al cuadrado, se extrae solo la base del término para revisar.
if ft.is_Pow:
ft = ft.as_base_exp()[0]
La multiplicación de funciones escalón μ(t)μ(t-1) se da cuando se aplica el integral de convolución entre x(t) y h(t), siendo x(t) un escalón. Sin embargo Sympy mantiene las expresiones sin simplificar, asunto a considerar en los siguientes ejercicios. por ahora se lo realiza con fcnm.simplifica_escalon(ft).
# Revisar causalidad de ft(t) en sympy # considera causal h(t)=b0*d + (modos caracteristicos)*u # Parte 1 comprueba solo impulso d(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t) # h = u # h = 3*sym.pi*u.subs(t,t-1) h = sym.exp(-2*t)*u.subs(t,t+1) # h = sym.exp(-2*t)*sym.cos(t) # h = 5 # h = u.subs(t,-t+2)*u.subs(t,-t+1) # h = u.subs(t,-t+1)*u.subs(t,-t+1) # h = 3*u.subs(t,-t+1)*u.subs(t,-t+1) # h = u.subs(t,t+1)*u.subs(t,-t+1) # h = u.subs(t,t-1)*u.subs(t,-t+2) # h = u.subs(t,t+2)*u.subs(t,-t-1) # h = u.subs(t,t-2)*u.subs(t,-t-1) # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 51 # PROCEDIMIENTO def es_causal(ft): ''' h(t) es causal si tiene b0*d(t)+u(t)*(modos caracterisicos) ''' def es_causal_impulso(ft): ''' un termino en lado derecho del plano ''' causal = False donde_d = fcnm.busca_impulso(ft) if len(donde_d)>0: # tiene impulso if donde_d[0]>=0: # derecha del plano causal = True return(causal) causal = True term_suma = sym.Add.make_args(ft) for term_k in term_suma: if term_k.has(sym.Heaviside): term_k = fcnm.simplifica_escalon(term_k) # h(t-a)*h(t-b) causal_k = True donde_u = fcnm.busca_escalon(term_k) if len(donde_u)==0: # sin escalon? causal_k = False if len(donde_u)==1: sentido1 = donde_u[0][0] donde1 = donde_u[0][1] # en lado izquierdo del plano if donde1<0 or sentido1<0: causal_k = False if len(donde_u)==2: donde1 = donde_u[0][0] sentido1 = donde_u[0][1] donde2 = donde_u[1][0] sentido2 = donde_u[1][1] # rectangulo lado derecho del plano if (donde1<donde2): if donde1<0: # u(t+1)*u(-t+1) causal_k = False if (donde2<donde1): if donde2<0: # u(-t+1)*u(t+1) causal_k = False else: # un termino, sin escalon unitario # causal depende si tiene un impulso causal_k = es_causal_impulso(term_k) causal = causal and causal_k return(causal) hcausal = es_causal(h) # SALIDA print('h(t):') sym.pprint(h) print('busca_impulso(ft):', fcnm.busca_impulso(h)) print('busca_escalon(ft):', fcnm.busca_escalon(h)) print('xcausal: ',hcausal) # Grafica figura_h = fcnm.graficar_ft(h,t_a,t_b,f_nombre='h') plt.show()
Ejemplo 4. Revisa si f(t) es causal de varios término de suma
Referencia: Ejercicio Lathi 2.6-3 p206, Lathi Ej. 2.12 p185,
Finalmente la revisión de la expresión f(t) revisa cada uno de los terminos de una suma. Dentro de cada termino de la suma se revisa cada factor que multiplica. Dentro de cada factor que multiplica de analiza si se encuentra un escalón o impulso unitario que opere solo en el lado derecho del plano.
Las expresiones usadas para revisar el ejercicio son
# entrada x(t) # h = u + d # h = 3*sym.pi*u.subs(t,t-1)+ 2*d # h = sym.exp(-2*t)*u.subs(t,t+1) + sym.exp(-4*t)*u.subs(t,t-3) # h = sym.exp(-2*t)*sym.cos(t) + 4 # h = 5 # h = u.subs(t,-t+2)*u.subs(t,-t+1) # h = u.subs(t,-t+1)*u.subs(t,-t+1) # h = 3*u.subs(t,-t+1)*u.subs(t,-t+1) h = u.subs(t,t-1)-u.subs(t,t-2)
el resultado del algoritmo para el ejercicio corresponde a:
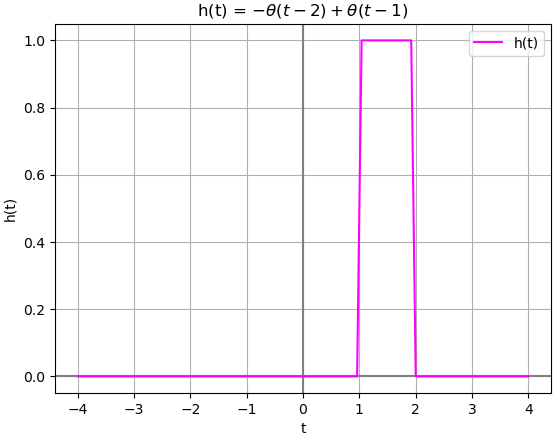
h(t): -Heaviside(t - 2) + Heaviside(t - 1) busca_impulso(ft): [] busca_escalon(ft): [[1 1] [2 1]] hcausal: True
La gráfica correspondiente que permite comprobar visualmente el resultado es
Instrucciones en Python
El algoritmo básicamente realiza el seguimiento de los resultados que se obtienen con las funciones de las secciones anteriore para cada término de suma.
# Revisar causalidad de ft(t) en sympy # considera causal h(t)=b0*d + (modos caracteristicos)*u # Parte 1 comprueba solo impulso d(t) import numpy as np import matplotlib.pyplot as plt import sympy as sym equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] import telg1001 as fcnm # INGRESO t = sym.Symbol('t',real=True) u = sym.Heaviside(t) d = sym.DiracDelta(t) # entrada x(t) # h = u + d # h = 3*sym.pi*u.subs(t,t-1)+ 2*d # h = sym.exp(-2*t)*u.subs(t,t+1) + sym.exp(-4*t)*u.subs(t,t-3) # h = sym.exp(-2*t)*sym.cos(t) + 4 # h = 5 h = u.subs(t,t-1)-u.subs(t,t-2) # grafica intervalo [t_a,t_b] simetrico a 0 t_b = 4 ; t_a = -t_b muestras = 51 # PROCEDIMIENTO hcausal = fcnm.es_causal(h) # SALIDA print('h(t):') sym.pprint(h) print('busca_impulso(ft):', fcnm.busca_impulso(h)) print('busca_escalon(ft):', fcnm.busca_escalon(h)) print('xcausal: ',hcausal) # Grafica figura_h = fcnm.graficar_ft(h,t_a,t_b,f_nombre='h') plt.show()