Referencia: Lathi Ejemplo 5.5 p510
continuando con la solución del ejercicio de condiciones iniciales,
y[n+2] – 5 y[n+1] + 6 y[n] = 3 x[n+1] + 5 x[n]
con las condiciones iniciales y[-1]=11/16, y[-2]=37/36,
ante una entrada x[n]=(-2)-nμ[n]
| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
En el ejemplo se encuentra que la solución total de la ecuación de diferencias se puede separar en dos componentes. El primero es generado por las condiciones iniciales y el segundo por la entrada x[n]
\Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] + \Bigg(-3 + \frac{11}{z} \Bigg) = 3\frac{1}{z-0.5}+5\frac{1}{z(z-0.5)} \Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = - \Bigg(-3 + \frac{11}{z} \Bigg) + \frac{3z+5}{z(z-0.5)} \Bigg(1 - 5 \frac{1}{z} + 6 \frac{1}{z^2}\Bigg) Y[z] = -\text{condiciones iniciales} + \text{entrada x[n]}para simplificar, se multiplica ambos lados por z2
(z^2 - 5 z + 6 ) Y[z] = - z(-3z +11) + \frac{z(3z+5)}{(z-0.5)} (z^2 - 5 z + 6 ) Y[z] = - \text{condiciones iniciales} + \text{entrada x[n]} Y[z] = \frac{- z(-3z +11)}{(z^2 - 5 z + 6 )} + \frac{z(3z+5)}{(z-0.5)(z^2 - 5 z + 6 ) }respuesta total = (respuesta a entrada cero) + (respuesta estado cero)
continuando luego con el proceso de fracciones parciales y cambio al dominio de tiempo discreto. (realizado en desarrollo analítico), aqui se usa la transformada_z inversa con Sympy:
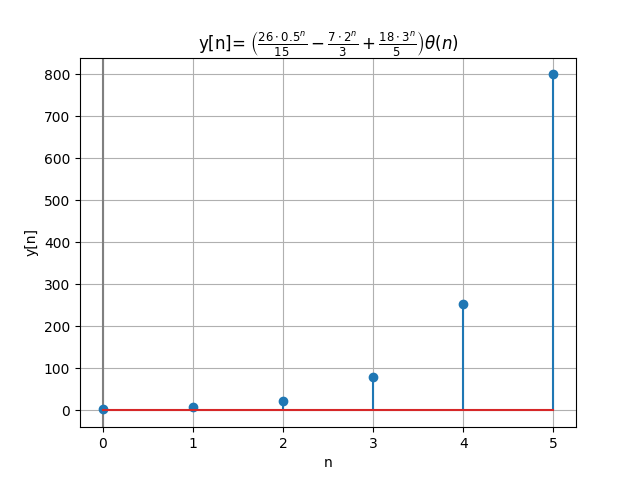
y[n] = \Bigg[ \frac{26}{15}(0.5)^n - \frac{7}{3}(2)^n + \frac{18}{5}(3)^n \Bigg] \mu [n]Instrucciones en Python
Se reutilizan los algoritmos de la sección LTID Transformada z – Fracciones parciales con Python a lo que se añaden las instrucciones de los pasos anteriores.
Hz {polos:veces} : {3: 1, 2: 1}
Hz {ceros:veces} : {-5/3: 1}
termino condiciones iniciales:
z*(11 - 3*z)
termino entrada x[n]:
2*z*(3*z + 5)
-------------
2*z - 1
Yz = ZIR_z + ZSR_z:
z*(11 - 3*z) 2*z*(3*z + 5)
- ------------ + ------------------------
2 / 2 \
z - 5*z + 6 (2*z - 1)*\z - 5*z + 6/
Yz en fracciones parciales z:
26*z 7*z 18*z
------------ - --------- + ---------
15*(z - 1/2) 3*(z - 2) 5*(z - 3)
y[n]:
/ n n n\
|26*0.5 7*2 18*3 |
|------- - ---- + -----|*Heaviside(n)
\ 15 3 5 /
>>>
Instrucciones Python
# Transformada z - Fracciones parciales # Y(z) = -condicion0+entradaxn = ZIR+ZSR # Lathi Ejemplo 5.5 p510 import sympy as sym import telg1001 as fcnm sym.SYMPY_DEBUG=True # INGRESO z = sym.Symbol('z') n = sym.Symbol('n', real=True) # coeficientes como racional en dominio 'ZZ' enteros a0 = sym.Rational(1/2).limit_denominator(1000) # señal de entrada Xz Xz = z/(z-a0) # Hz = Pz/Qz Pz = 3*z+5 Qz = z**2-5*z+6 Hz = Pz/Qz # condiciones iniciales ascendente ...,y[-2],y[-1] a1 = sym.Rational(37,36) a2 = sym.Rational(11,6) cond_inicio = [a1, a2] # PROCEDIMIENTO Fz = sym.simplify(Hz) # polos y ceros de Fz [P,Q] = Fz.as_numer_denom() P = sym.poly(P,z) Q = sym.poly(Q,z) P_ceros = sym.roots(P) Q_polos = sym.roots(Q) # coeficientes QD Q_coef = Q.coeffs() Q_grado = Q.degree() # Términos de condiciones iniciales m0 = len(cond_inicio) term_0 = 0 for j in range(0,Q_grado,1): term_grado = 0 for i in range(m0-1-j,m0,1): term_cond0 = cond_inicio[i]*(z**((m0-1-j)-i )) term_grado = term_grado + term_cond0 term_0 = term_0 + term_grado*Q_coef[j+1] # salida y(t) a entrada x(t) term_0 = sym.simplify(term_0*(z**2)) term_xn = sym.simplify(Pz*Xz) ZIR_z = -sym.simplify(term_0/Q) ZSR_z = sym.simplify(term_xn/Q) # Y[z] = entrada0 + estado0 Yz = ZIR_z + ZSR_z # Y[z] en fracciones parciales y parametros cuadraticos Yzp = fcnm.apart_z(Yz) Qs2 = fcnm.Q_cuad_z_parametros(Yzp) # Inversa de transformada z yn = 0*n ; Fz_revisar = [] term_sum = sym.Add.make_args(Yzp) for term_k in term_sum: term_kn = fcnm.inverse_z_transform(term_k,z,n) if type(term_kn)==tuple: yn = yn + term_kn[0] else: yn = yn + term_kn yn = yn.collect(sym.Heaviside(n)) yn = yn.collect(sym.DiracDelta(n)) yn = fcnm._round_float_is_int(yn) # SALIDA print(' Hz {polos:veces} : ',Q_polos) print(' Hz {ceros:veces} : ',P_ceros) print('\n termino condiciones iniciales: ') sym.pprint(term_0) print(' termino entrada x[n]: ') sym.pprint(term_xn) print('\n Yz = ZIR_z + ZSR_z:') sym.pprint(Yz) print('\n Yz en fracciones parciales z:') sym.pprint(Yzp) if len(Qs2)>0: print('Y[z] parametros cuadraticos: ') for Qs2_k in Qs2: print(Qs2_k,':') for cadauno in Qs2[Qs2_k].keys(): print(cadauno,'\t',Qs2[Qs2_k][cadauno]) print('\n y[n]:') sym.pprint(yn) if len(Fz_revisar)>0: print('\n --- revisar terminos sin transformada en tabla: ---') for un_term in Fz_revisar: print(un_term)