Referencia: Lathi 6.1 p593, Oppenheim 3.3 p186 Chapra 5ed 19.2 p546
La serie de Fourier aproxima una señal o función contínua mediante una serie infinita de sinusoides.
f(t) = a_0 + \sum_{k=1}^{\infty}[a_k \cos( k \omega_0 t) + b_k \sin(k \omega_0t)]donde los coeficientes de la ecuación se calculan como:
a_k = \frac{2}{T} \int_0^T f(t) \cos(k \omega_0 t) \delta t b_k = \frac{2}{T} \int_0^T f(t) \sin(k \omega_0 t) \delta talgoritmo: [ integral con Sympy ] [ instrucción Sympy ]
Ejemplo. Serie de Fourier de rectángulo(t) con Integral de Sympy
Referencia: Lathi 6.5 p617, Chapra 5ed Ejemplo 19.2 p548
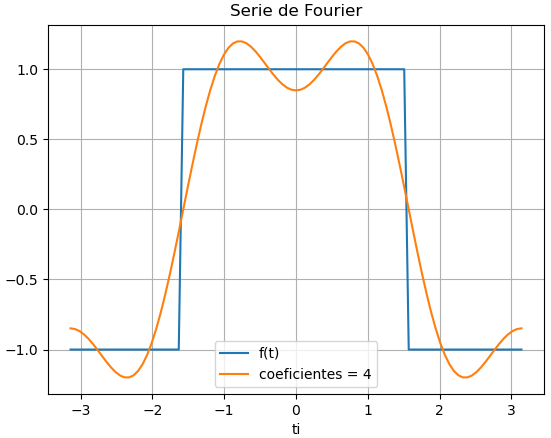
Utilice la serie de Fourier continua para aproximar la función de onda cuadrada o rectangular. Para el cálculo del ejemplo se usará hasta 4 términos de la serie.
f(t) = \begin{cases} -1 && -T/2<t<-T/4 \\ 1 && -T/4<t<T/4 \\ -1 && T/4<t<T/2 \end{cases}Coeficientes ak y bk
Para determinar las expresiones de los coeficientes, en Python se usa la librería Sympy que nos facilita el desarrollo las fórmulas simbólicas ak y bk.
Si requiere revisar el concepto se adjunta el enlace:
Fórmulas y funciones simbólicas con Python – Sympy
El desarrollo a papel y lápiz se deja como tarea.
Usando Python se obtiene los siguientes resultados:
expresión ak: / / /pi*k\ \ |2*|2*sin|----| - sin(pi*k)| | \ \ 2 / / <--------------------------- for And(k > -oo, k < oo, k != 0 | pi*k | \ 0 otherwise expresión bk: 0
usando formato latex para la expresión, generado por Sympy se obtiene:
\begin{cases} \frac{2 \cdot \left(2 \sin{\left(\frac{\pi k}{2} \right)} - \sin{\left(\pi k \right)}\right)}{\pi k} & \text{for}\: \left(k > -\infty \vee k > 0\right) \wedge \left(k > -\infty \vee k < \infty\right) \wedge \left(k > 0 \vee k < 0\right) \wedge \left(k < 0 \vee k < \infty\right) \\0 & \text{otherwise} \end{cases} b_k = 0Instrucciones en Python
# Serie de Fourier, con n coeficientes # Ref.Chapra 5ed Ejemplo 19.2 p548/pdf572 import sympy as sym # INGRESO t = sym.Symbol('t') T0 = 2*sym.pi ; t0 = -T0/2 # periodo ; t_inicio ft = sym.Piecewise((-1,t <-T0/2), (-1,t <-T0/4), ( 1,t < T0/4), (-1,t < T0/2), (-1,True),) n = 4 # número de coeficientes # PROCEDIMIENTO w0 = 2*sym.pi/T0 k = sym.Symbol('k') # Términos ak para coseno() enintegral = ft*sym.cos(k*w0*t) yaintegrado = sym.integrate(enintegral,(t,t0,t0 + T0)) Fak = (2/T0)*yaintegrado Fak = sym.simplify(Fak) # Términos bk para seno() enintegral = ft*sym.sin(k*w0*t) yaintegrado = sym.integrate(enintegral,(t,t0,t0 + T0)) Fbk = (2/T0)*yaintegrado Fbk = sym.simplify(Fbk) # SALIDA print(' expresión ak:') sym.pprint(Fak) print('\n ak formato latex') print(sym.latex(Fak)) print('\n expresión bk:') sym.pprint(Fbk) print('\n bk formato latex') print(sym.latex(Fbk))
Evaluación de coeficientes
Con las expresiones obtenidas en el bloque anterior, se evalúan los n coeficientes ak y bk, substituyendo en las expresiones los valores en cada índice i y se obtiene como resultado:
coeficientes ak,bk: k_i : [0, 1, 2, 3] ak : [0, 4/pi, 0, -4/(3*pi)] bk : [0, 0, 0, 0]]
Instrucciones Python
Las instrucciones son adicionales al bloque anterior. La evaluación se mantiene usando las expresiones simbólicas usando la instrucción .subs()
# evalua los coeficientes a0 = Fak.subs(k,0)/2 b0 = Fbk.subs(k,0) ak = [a0] ; bk = [b0] ; k_i = [0] i = 1 while not(i>=n): ak_valor = Fak.subs(k,i) bk_valor = Fbk.subs(k,i) ak.append(ak_valor) bk.append(bk_valor) k_i.append(i) i = i+1 print('\n coeficientes ak,bk: ') for uncoef in coef_fourier: print(uncoef,':',coef_fourier[uncoef])
Expresión de la Serie de Fourier
Encontrados los coeficientes ak y bk, se los usa en la expresión principal
f(t) = a_0 + \sum_{k=1}^{\infty}[a_k \cos( k \omega_0 t) + b_k \sin(k \omega_0t)]obteniendo la siguiente expresión para la serie de Fourier como fs(t)
serie de Fourier fs(t): 4*cos(t) 4*cos(3*t) -------- - ---------- pi 3*pi
Instrucciones en Python
Las instrucciones se añaden a continuación de los bloques anteriores,
# serie de Fourier serieF = ak[0] + 0*t i = 1 while not(i>=n): serieF = serieF + ak[i]*sym.cos(i*w0*t) serieF = serieF + bk[i]*sym.sin(i*w0*t) i = i+1 print('\n serie de Fourier f(t): ') sym.pprint(serieF)
Gráficas de f(t) y Serie de Fourier
Para comparar la función f(t) con la aproximación en series de Fourier, se usa el intervalo [a,b] con una cantidad de muestras usando la instrucción np.linspace() y guardando el resultado en ti.
Para evaluar los puntos ti en cada expresión, por simplicidad se convierte la expresión de su forma simbólica a numérica lambda, usando sym.lambdify()
Instrucciones en Python
Las instrucciones para graficar las series de Fourier van a continuación de las anteriores,
# Grafica --------------------- import numpy as np import matplotlib.pyplot as plt # Evaluación para gráfica f_t = sym.lambdify(t,ft) serie_ft = sym.lambdify(t,serieF) ti = np.linspace(float(t_a),float(t_b),muestras) fi = f_t(ti) serie_fi = serie_ft(ti) # Grafica de Serie de Fourier plt.plot(ti,fi,label = 'f(t)') etiqueta = 'coeficientes = '+ str(n) plt.plot(ti,serie_fi,label = etiqueta) plt.xlabel('ti') plt.legend() plt.grid() plt.title('Serie de Fourier f(t); T0='+str(T0)) plt.show()
Tarea: Realizar el ejercicio, aumentando el número de términos a 8
Espectro de Fourier de amplitud y fase
Referencia: Lathi 6.1 p599, Chapra 19.3 p551
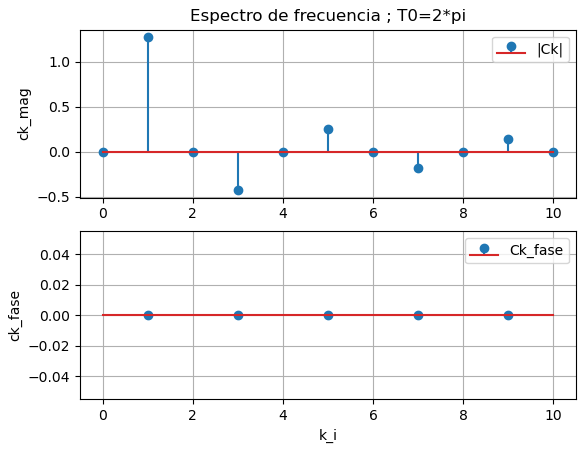
Los espectros ofrecen información que no aparece en el dominio del tiempo. La gráfica de frecuencias ofrece una representación rápida de la estructura de armónicas, que son como las huellas dactilares que ayudan a caracterizar y entender la forma de una señal complicada.
La gráfica considera todas las magnitudes como positivas. Posteriormente se puede observar como en algunos textos que se incorpora el signo en la grafica de magnitud. En la siguiente sección se trata más éste detalle.
Para mostrar este espectro de frecuencias se incrementó el número de términos de la serie a n=11, para observar mejor la forma de la gráfica.
# espectro de frecuencias k ak_i = np.array(ak,dtype=float) bk_i = np.array(bk,dtype=float) ck_mag = np.sqrt(ak_i**2 + bk_i**2) ck_fase = np.arctan(-bk_i/ak_i) revisa0 = (abs(ak_i)>=casicero) pendiente = -bk_i[revisa0]/ak_i[revisa0] ck_fase[revisa0] = np.arctan(pendiente) coef_fourier['ck_mag'] = ck_mag coef_fourier['ck_fase'] = ck_fase print('\n coeficientes ak,bk,Ck_mag,Ck_fase: ') for uncoef in coef_fourier: print(uncoef,':',coef_fourier[uncoef]) # grafica de espectro de frecuencia plt.subplot(211) plt.stem(k_i,ck_mag,label='|Ck|') plt.ylabel('ck_mag') plt.title('Espectro de frecuencia ; T0='+str(T0)) plt.legend() plt.grid() plt.subplot(212) plt.stem(k_i,ck_fase,label='Ck_fase') plt.legend() plt.ylabel('ck_fase') plt.xlabel('k_i') plt.grid() plt.show()
El algoritmo final como una integración de las partes presentadas se usa en la página siguiente con algunos ejemplos tradicionales de la transformada de Fourier.
Instrucciones Python para Integral de la serie de Fourier con n coeficientes
Se integran todas las partes anteriores en un algoritmo
# Serie de Fourier, con n coeficientes # Ref.Chapra 5ed Ejemplo 19.2 p548/pdf572 import sympy as sym import numpy as np # INGRESO t = sym.Symbol('t') T0 = 2*sym.pi ; t0 = -T0/2 # periodo ; t_inicio ft = sym.Piecewise((-1,t <-T0/2), (-1,t <-T0/4), ( 1,t < T0/4), (-1,t < T0/2), (-1,True),) n = 4 # número de coeficientes t_a = t0 # intervalo de t =[t_a,t_b] t_b = t0 + T0 muestras = 101 # 51 resolucion grafica casicero = 1e-10 # PROCEDIMIENTO w0 = 2*sym.pi/T0 k = sym.Symbol('k') # Términos ak para coseno() enintegral = ft*sym.cos(k*w0*t) yaintegrado = sym.integrate(enintegral,(t,t0,t0 + T0)) Fak = (2/T0)*yaintegrado Fak = sym.simplify(Fak) # Términos bk para seno() enintegral = ft*sym.sin(k*w0*t) yaintegrado = sym.integrate(enintegral,(t,t0,t0 + T0)) Fbk = (2/T0)*yaintegrado Fbk = sym.simplify(Fbk) # evalua los coeficientes a0 = Fak.subs(k,0)/2 b0 = Fbk.subs(k,0) ak = [a0] ; bk = [b0] ; k_i = [0] i = 1 while not(i>=n): ak_valor = Fak.subs(k,i) bk_valor = Fbk.subs(k,i) ak.append(ak_valor) bk.append(bk_valor) k_i.append(i) i = i+1 coef_fourier = {'k_i': k_i, 'ak' : ak, 'bk': bk} # serie de Fourier serieF = ak[0] + 0*t i = 1 while not(i>=n): serieF = serieF + ak[i]*sym.cos(i*w0*t) serieF = serieF + bk[i]*sym.sin(i*w0*t) i = i+1 # espectro de frecuencias k ak_i = np.array(ak,dtype=float) bk_i = np.array(bk,dtype=float) ck_mag = np.sqrt(ak_i**2 + bk_i**2) ck_fase = np.arctan(-bk_i/ak_i) revisa0 = (abs(ak_i)>=casicero) pendiente = -bk_i[revisa0]/ak_i[revisa0] ck_fase[revisa0] = np.arctan(pendiente) coef_fourier['ck_mag'] = ck_mag coef_fourier['ck_fase'] = ck_fase # SALIDA print(' expresión ak:') sym.pprint(Fak) print('\n ak formato latex') print(sym.latex(Fak)) print('\n expresión bk:') sym.pprint(Fbk) print('\n bk formato latex') print(sym.latex(Fbk)) print('\n serie de Fourier f(t): ') sym.pprint(serieF) print('\n coeficientes ak,bk,Ck_mag,Ck_fase: ') for uncoef in coef_fourier: print(uncoef,':',coef_fourier[uncoef]) # Grafica --------------------- import matplotlib.pyplot as plt # Evaluación para gráfica f_t = sym.lambdify(t,ft) serie_ft = sym.lambdify(t,serieF) ti = np.linspace(float(t_a),float(t_b),muestras) fi = f_t(ti) serie_fi = serie_ft(ti) # Grafica serie de Fourier fig_serieF, graf_sF = plt.subplots() graf_sF.plot(ti,fi,label = 'f(t)') etiqueta = 'coeficientes = '+ str(n) graf_sF.plot(ti,serie_fi,label = etiqueta) graf_sF.set_xlabel('ti') graf_sF.legend() graf_sF.grid() graf_sF.set_title('Serie de Fourier f(t); T0='+str(T0)) # plt.show() # grafica de espectro de frecuencia fig_espectro, graf_sptr = plt.subplots(2,1) graf_sptr[0].stem(k_i,ck_mag,label='|Ck|') graf_sptr[0].set_ylabel('ck_mag') graf_sptr[0].set_title('Espectro de frecuencia ; T0='+str(T0)) graf_sptr[0].legend() graf_sptr[0].grid() graf_sptr[1].stem(k_i,ck_fase,label='Ck_fase') graf_sptr[1].legend() graf_sptr[1].set_ylabel('ck_fase') graf_sptr[1].set_xlabel('k_i') graf_sptr[1].grid() plt.show()
algoritmo: [ integral con Sympy ] [ instrucción Sympy ]
…
Instrucción Sympy para Serie de Fourier
Usando el ejercicio 1, se muestra el resultado obtenido usando la instrucción incorporada en Sympy. La función truncate(n) aplicada a la serie, permite obtener los n términos no cero. Existen operaciones adicionales para desplazamiento y escala en x que evitan tener que realizar las operaciones nuevamente y optimizan el tiempo del algoritmo
serie de Fourier f(t):
4*cos(t) 4*cos(3*t) 4*cos(5*t)
-------- - ---------- + ---------- + ...
pi 3*pi 5*pi
serie de Fourier f(t), n términos:
/pi\ /3*pi\
4*cos(t)*sinc|--| 4*cos(3*t)*sinc|----|
\4 / \ 4 /
----------------- - ---------------------
pi 3*pi
serie de Fourier f(t), k términos no cero:
4*cos(t) 4*cos(3*t) 4*cos(5*t) 4*cos(7*t)
-------- - ---------- + ---------- - ----------
pi 3*pi 5*pi 7*pi
>>>
Instrucciones en Python
# Serie de Fourier, con n coeficientes # Ref.Chapra 5ed Ejemplo 19.2 p548/pdf572 import sympy as sym # INGRESO t = sym.Symbol('t') T0 = 2*sym.pi ; t0 = 0 # periodo ; t_inicio ft = sym.Piecewise((-1,t <-T0/2), (-1,t <-T0/4), ( 1,t < T0/4), (-1,t < T0/2), (-1,True),) n = 4 # número de coeficientes t_a = t0 # intervalo de t =[t_a,t_b] t_b = t0 + T0 # PROCEDIMIENTO serieF = sym.fourier_series(ft,(t,t0,t0+T0)) serieFn = sym.expand(serieF.sigma_approximation(n)) serieFk = serieF.truncate(n) # SALIDA print('\n serie de Fourier f(t): ') sym.pprint(serieF) print('\n serie de Fourier f(t), n términos: ') sym.pprint(serieFn) print('\n serie de Fourier f(t), k términos no cero: ') sym.pprint(serieFk)
Adicionalmente incorpora otras operaciones para el dominio de la frecuencia como desplazamiento y escalamiento en x
>>> sym.pprint(serieF)
4*cos(t) 4*cos(3*t) 4*cos(5*t)
-------- - ---------- + ---------- + ...
pi 3*pi 5*pi
>>> sym.pprint(serieF.scalex(2))
4*cos(2*t) 4*cos(6*t) 4*cos(10*t)
---------- - ---------- + ----------- + ...
pi 3*pi 5*pi
>>> sym.pprint(serieF.shiftx(2))
4*cos(t + 2) 4*cos(3*t + 6) 4*cos(5*t + 10)
------------ - -------------- + --------------- + ...
pi 3*pi 5*pi
>>>
algoritmo: [ integral con Sympy ] [ instrucción Sympy ]